


 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|||||||||
 | ||||||||||
|
||||||||||
|
||||||||||
|
misof wins Room 3
ModeProbabilityby brett1479Here we must compute the probability that a given number will occur most frequently. The friendly constraints guarantee there will be at most 5 different values, and at most 15 numbers generated. Looping through all possible counts for each value, we see there are at most C(19,4)=3876 (read "19 choose 4") ways to choose the values. If we only consider the ways where the required number occurs most frequently, there are even fewer possibilities to consider. For each set of counts, we can compute the probability of that set occurring. First, fix a particular ordering of the multiset we have chosen (a multiset is a collection of values with different counts). To compute the probability of that ordering, we multiply the probability of getting each value. For example, if
probs = {20,30,50}
and we are considering the multiset
M = { 0 with count 2, 1 with count 1, 2 with count 3 }
with fixed ordering <2,0,1,0,2,2>, then the associated probability is
P = .5*.2*.3*.2*.5*.5Conveniently, any ordering of these 6 values will occur with the same probability, so the total probability for this set of counts can be computed by multiplying P by the number of orderings of these values. This count is C = 6!/(2!*1!*3!) = 606! represents the number of ways to order 6 distinct objects. The denominator accounts for the duplicates. This formula is called a multinomial coefficient. To complete the task at hand, we sum all of the C*P values (for each possible set of counts), and get our final result. Conferenceby lbackstromIt is useful to think about what happens when n = 1: there is only 1 person and he wants to attend as many meetings as possible. In this case, a simple greedy algorithm is correct. First go to the meeting that gets out earliest. Then, among meetings that are still options, go the the one that gets out earliest, and so on. By always picking the meeting that gets out earliest, you maximize your potential to go to future meetings. It turns out that you can extend this to the case where n > 1. By having someone go to the meeting that gets out earliest, you maximize that person's ability to go to future meetings. As long as you iteratively assign the meetings, always picking the one that ends earliest out of your available options, you'll end up covering the most meetings possible. All that remains is to figure out which meetings are still possible, given that some meetings have already been selected. One way to do this is to assign people to meetings as the meetings are selected. Number the people from 1 to n, and whenever you select a meeting, assign it to the person who is done with other meetings latest, but doesn't have a conflict with that meeting. If you do this, you will always assign the meetings to people in such a way that you are maximizing the ability of the group to go to future meetings. Then, during the execution of your algorithm, a meeting is an option if and only if there is some person who doesn't have any conflict with it, assuming that you assign meetings in order by ending time. Note that one incorrect way to do this (which cost many coders), is to simply count the number of conflicts that each meeting has with previously assigned meetings. While this is temptingly simple, it has the unfortunate property that it fails. Image a meeting from 8-9, 9-10 and 8:30-11, and two people. We examine the meetings in order by end time, and find that we can go to both of the first two meetings. Now, we look at the 8:30-11 meeting and see that it conflicts with two previously assigned meetings. Hence, we erroneously conclude that we can't go to the third meeting also. DiscCoverby gepaIt is easier here to solve the inverse problem, i.e., what is the maximum radius of a disc that we can cover with numDiscs unit discs (radius 1.0). If we have found that, we can scale the solution to the given discRadius, and deduce thus the minimum radius we need for the small discs.
Let's call the maximum radius of a disc that we can cover
using n unit discs
double minRadius(double discRadius, int numDiscs) {
double[] maxRadius = new double[numDiscs + 1];
maxRadius[0] = 0.0;
maxRadius[1] = 1.0; // just one disc
maxRadius[2] = 1.0; // a second disc does not help much
for (int n = 3; n <= numDiscs; n++) {
// We initialize first maxRadius[n] to the worst value we
// know that we can achieve.
maxRadius[n] = maxRadius[n - 1]
for (int m = 3; m <= n; m++) {
// addRing(double r0, int m) returns the maximum radius
// we can cover if we already have a disc with radius r0
// covered and add m discs covering an additional ring
// (see below for implementation details).
double rnext = addRing(maxRadius[n - m], m);
if (rnext > maxRadius[n]) {
maxRadius[n] = rnext;
}
}
}
// With numDiscs discs of radius 1.0 we can cover a disc of radius maxRadius[numDiscs]
// So, we can cover a disc of radius discRadius using numDiscs discs of radius:
return discRadius / maxRadius[numDiscs];
}
Now remains the hard part, implementing the function 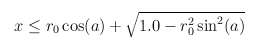 Note that if the term under the square root is negative, i.e., r0 * sin(a) > 1.0, we can not cover the circle r0 with only m additional discs, so we just return r0. 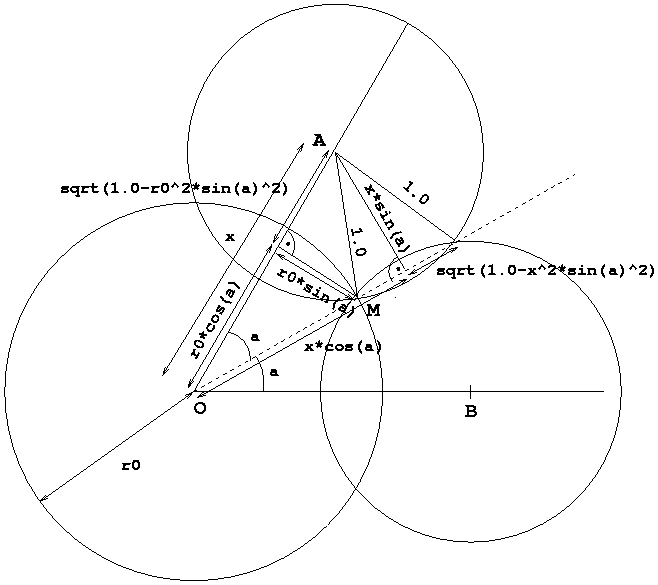 If we place the discs at a distance x, we cover a ring up to an outer radius (see figure): 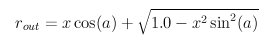 We want to find the x that maximises this, so the derivative of this term must be set to 0 (to ensure that this is actually a maximum we need to also check the second derivative, but this turns out to be always negative, so we do indeed have a maximum): 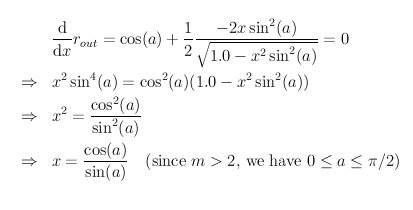 If this is within the limit given above for x, then this is the value we need to take for x, otherwise we have to use the maximum allowed x value as given above. Using the formula for rout we can finally return the radius of the disc we can cover with m discs additional to the already covered r0 disc.
In total, we end up with the following code (in Java)
for
double addRing(double r0, int m) {
double a = Math.PI / m;
double z = 1.0 - r0 * r0 * Math.sin(a) * Math.sin(a);
if (z < 0) return r0;
double xmax = r0 * Math.cos(a) + Math.sqrt(z);
double x = Math.cos(a) / Math.sin(a);
if (x > xmax) x = xmax;
return x * Math.cos(a) + Math.sqrt(1.0 - x * x * Math.sin(a) * Math.sin(a));
}
|




|