


 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|||||||||
 | ||||||||||
|
||||||||||
|
||||||||||
|
Eryx is the new Algorithm Champion
SuperKingby gepaLet's split the problem into three different sub-problems, depending on the value of type1. The case type1=0, where we only perform Type-2 moves, is the easiest one. Here, the answer is the number of possible landing squares after performing type2 steps of a normal random walk on a two-dimensional lattice, the lattice points being the board squares at a distance (2x, 2y) relative to the starting square. It is easy to see (see figure below for type2=3, the dot in the middle marks the starting square), that the possible landing squares are arranged in a square structure of (type2+1)2 squares (the red ones). 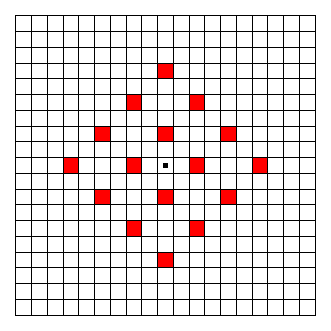 For type1=1 we have to perform one additional Type-1 step beginning from the landing squares of the previous case. This leads initially to a value 8 * (type2+1)2 (because there are 8 possible Type-1 moves), but we have to be careful since we have counted some squares twice. The figure below shows how we can count the squares that were counted twice, in order to correct the return value. For the figure, type2 has been chosen to be 3 again. The landing squares after the Type-2 moves are shown in red. After the final Type-1 move, the possible landing squares are shown in green. The dark green ones are the ones we counted twice. To each "internal" red square correspond 4 dark green squares (there are a total of (type2-1)2 such red squares). To each red square on a corner of the (type2+1) x (type2+1) square (4 corners in total) correspond 2 dark green squares, and to each red square on an edge of the (type2+1) x (type2+1) square correspond 3 dark green squares (there are 4 * (type2-1) such red squares). And since we count each dark green square twice, we have to divide again by two, for a total of: (4 * (type2-1)2 + 2 * 4 + 3 * 4 * (type2-1)) / 2 dark green squares in total. If we subtract this value from 8 * (type2+1)2 and simplify the term, we get the total number of green squares (now also the dark green squares correctly counted only once): 6 * type22 + 14 * type2 + 8 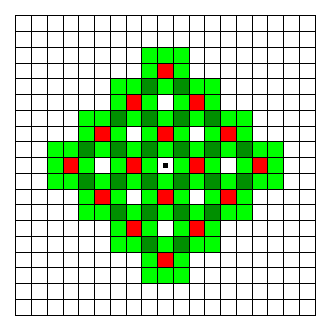 Now let's come to the difficult case, type1>1. It is easiest to explain the final formula using an example type1=2, type2=3 (see figure below). Notice, that it is not important in which order we perform the moves, so we will perform the Type-1 moves first here. After type1(>1) Type-1 moves we can land in any of the green squares shown in the figure below (the starting square is again the square with a dot at the center of this area). These are all squares having a distance of maximum type1 to the x- or y-direction from the starting square, which leads to the green square with dimensions (2*type1+1) times (2*type1+1). From this, if we do the remaining type2 Type-2 moves only up or down, we can cover (additionally to the green area) the squares in the red area. If one of the Type-2 moves is to the left or right, we can additionally reach the blue area, if two of the Type-2 moves are to the left or right, we can additionally reach the yellow area and so on. The central (green and red) area has width (2*type1+1) and height (2*type1+1+4*type2), the next areas (blue, yellow etc.) have each width 4 (2 to the left and 2 to the right of the green/red area) and height decreasing by 4 each time up to a minimum of (2*type1+1). If we define A:=(2*type1+1) we have a total of:
result = 4 * (A + (A + 4) + (A + 8) + ... + (A + 4 * type2 - 4))
+ A * (A + 4 * type2)
= 4 * A * type2 + 4 * 4 * (0 + 1 + 2 + ... + (type2 - 1))
+ A * (A + 4 * type2)
= 4 * A * type2 + 8 * (type2 - 1) * type2 + A * (A + 4 * type2)
reachable squares. If we insert the value for A from above (A=2*type1+1) and simplify the term, we finally get: result = 4 * type12 + 8 * type22 + 16 * type1 * type2 + 4 * type1 + 1 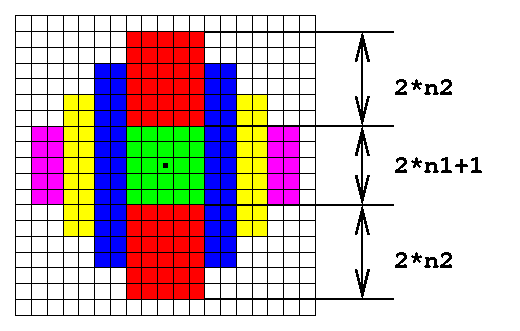 In total we have the following solution:
if (type1 == 0) {
return (type2 + 1) * (type2 + 1);
} else if (type1 == 1) {
return 6 * type2 * type2 + 14 * type2 + 8;
} else {
return 4 * type1 * type1 + 8 * type2 * type2 + 16 * type1 * type2 + 4 * type1 + 1;
}
Instead of doing the analysis to come up with the above formulas, one can easily see after trying out some examples, that the result must be a quadratic formula in type1 and type2 for the case type1>1 (or just some quadratic formula in type2 for type1=1 and type1=0), and try to deduce the constant factors (a - f) of:
result = a * type1 * type1 + b * type1 * type2 + c * type2 * type2
+ d * type1 + e * type2 + f
The last example was a great help for this, immediately showing that a + b + c = 28, d + e = 4 and f = 1, so that with just some trying around with small examples, all factors could be deduced. NearBirthdaysby YarinProbability and combinatorics are often related. While this problem is formulated as a probability problem, it's easiest to solve it thinking in combinatoric terms: There are daysInAYearnoPeople possible birthday combinations. How many of them satisfy the constraint that no two persons are born within the given amount of days? Without loss of generality, we can assume that one person is born on the first day of the year. The number of days left to consider is then daysInAYear - 1 - 2*withinDays (call this M). If this is ? 0, obviously the likelihood that two persons are born within withinDays is 1.0. Now we should find the number of ways to assign birthdays to the remaining noPeople-1 persons in the M days available so the constraints are satisfied. This can be done by defining a recursive function. Define f(x,y) as a function which returns the number of ways to assign birthdays to x people in a y day consecutive time span (note that we don't have to worry about circularity because we have fixed one person on day 1). f(1,y) is of course easy to evaluate - there are y ways to place someone in a y day time span. To evaluate f(x,y), we decide (by looping over all values) which day in the y day time span that should be the next birthday for someone among the x people left (call this day i, 0 ≤ i < y). For each i, we calculate how many ways to assign birthdays to the remaining x-1 people in a y-i-withinDay time span. This value needs to be multiplied by y since anyone of the y people left could have been assigned birthday i. Once the math has been figured out, the function evaluation should be implemented using either memoization or dynamic programming. Finally, since we want probability, we should divide the result with daysInAYearnoPeople-1 (since we fixed the birthday for one person). It's safe to use double in this problem even though the numbers can get very large (if all the division is done at the end) since all calculations are stable. ShortTapsby YarinThe first thing one should realize is that all messages longer than interceptTime can always be sent at time 0. These messages can then be ignored for the rest of the solution. We only have to make sure that the returned answer is never less than the longest message. The maybe easiest way to figure out the solution is to consider how one would solve the problem had the constraint been that at most one message was allowed to be intercepted. If there are two messages to be sent (as stated above, from now on we assume that all messages are at most interceptTime long), we can always send them in interceptTime+1 minutes: one message is sent at time 0, the other message is sent so that it has finished receiving at time interceptTime+1. Assume now that we have k messages to send. The length of each message is t[k] and interceptTime is y. For now, we decide to send the messages in order. That is, message 1 is first sent, then message 2 is sent as soon as possible, then message 3 etc. How long time would it then take to send all messages? Let start[i] and stop[i] be the start and stop time when each message is being sent. Obviously we have that start[i]+t[i]=stop[i]. From the reasoning in the previous paragraph we also have that stop[i+1]=start[i]+y+1. So:
start[i] = stop[i] - t[i]
stop[i+1] = start[i] + (y+1)
stop[i+1] = stop[i] + (y+1) - t[i]
stop[k] = stop[k-1] + (y+1) - t[k-1] =
= stop[k-2] + (y+1) - t[k-1] + (y+1) - t[k-2] =
= ... =
= stop[1] + (k-1)*(y+1) - sum(x=1..k-1, t[x]) =
= t[1] + (k-1)*(y+1) - sum(x=1..k-1, t[x]) =
= (k-1)*(y+1) - sum(x=2..k-1, t[x])
And - surprise, surprise - the total transmission time only depends on the second to the second last message sent, and not at all in which order they are sent. As can be seen, the total transmission time becomes the shortest if the longest messages are put among message 2 to k-1. So we always want the two shortest messages to be sent first and last.
Now back to the original problem. We now need to find a way to partition the messages into three partitions. Each partition can then be sent independently of each other, and the time it takes to send them is given by the formula above. The total time will be the maximum of these three times. Since there will be a total of six messages that won't affect the overall time at all, we can take out the six shortest messages. The remainder of the problem is a classic dynamic programming problem: We have x objects (in this case at most 44 since 6 have been removed) that we want to split into three partitions so that the maximum sum in each partition is as small as possible. The weight of each object is not t[i] but y+1-t[i], as can be seen from the formula above. To solve the DP problem, let f(k,a,b) be true if it's possible to partition the first k objects into three partitions so that one partition has size a, another one size b and the third one sum(x=1..k,t[x]-a-b). f(k,a,b) is true if either f(k-1,a-t[k],b), f(k-1,a,b-t[k]) or f(k-1,a,b) is true (corresponding to placing object k in any of the three partitions). This function is most easily calculated using dynamic programming and not memoziation, because we won't easily be able to keep a cache of all values in memory at the same time due to the input constraints of message sizes. When using dynamic programming, old values can be overwritten that won't be used again (f(k,a,b) never refers to f(k-2,x,y) so the outer dimension can be stored in modulo 2). The final answer is found by looping over all partitions sizes (only two loops; the size of the third partition is calculated from the other two) and check the corresponding element in the recursive function. There are also some special cases to consider. If, after removing messages longer than interceptTime, we have at most 3 or at most 6 messages left, special case handling might be necessary to avoid wrong answer or run time errors. |




|