andrewzta wins the WildCard


Discuss this match
Thursday, May 4, 2006
Introduction by lbackstrom

The wildcard round has always proved to be one of the most exciting parts of TopCoder finals. The competitors are already all warmed up, and the competition is always extremely fierce. TCO '06 was certainly no exception and no one was sure what would happen until the system test finished.

Most of the 12 competitors breezed through the easy problem, almost all of them solving it in the first 15 minutes (it took po only 7). The medium problem proved quite difficult for everyone though. Only reid was able to submit it quickly, for 363 points. natori checked in next, but for only 281. ploh and andrewzta were not far behind, each submitting it with about half an hour to go. But, they would all have to hope reid would fail a problem, as he scored a solid 616 on the hard, and saved plenty of time to test his code and work on challenges. The other competitors were far from calling it quits though, as both andrewzta and SnapDragon submitted the hard problem in the final minutes of the round. Since reid had to resubmit the medium, this left andrewzta on top, followed by reid in second, and SnapDragon in third. Of the competitors with only easy and medium submissions, natori stood on top, over 100 points above the next coder.

The challenge phase was not so exciting as the coding phase, but it did result in ploh netting 75 points at the expense of reid and JongMan's mediums. Unfortunately for reid and SnapDragon, the dust had not settled yet, and the system testing phase brought down both of their hard submissions. This left andrewzta on top, with the only successful hard submission from any of the rounds so far. natori, the only one to successfully solve the medium problem, took second. Good luck to everyone in the finals tomorrow!

TrafficMonitor

by brett1479

The problem begins with an important structural consideration: each pair of nodes is connected by at most 1 path. This is another way of saying the underlying graph of the network is a forest. Since (non-trivial) forests always have leaves, we can use a leaf-driven approach to solve the task. The link connected to a leaf must be monitored, so this forces one of two vertices to have a monitor (the leaf or its neighbor).

It is always optimal to choose the leaf's neighbor (why?), so we do so, and remove all newly monitored edges from the network. This leaves a smaller network, which can be simiilarly solved (by induction).

BishopOnTheBoard

by Andrew_Lazarev

In case of k equals to 1, it is easy to calculate the answer by trying all possible moves. Let's find solution for cases k > 1. If x > 0, let's solve the problem for the parts of the board to the left of x and to the right independently. So now we can assume that the bishop stands at the leftmost column of the board.

Let's draw two polylines consisting of k segments each from the initial position of the bishop, like it is shown on the figure.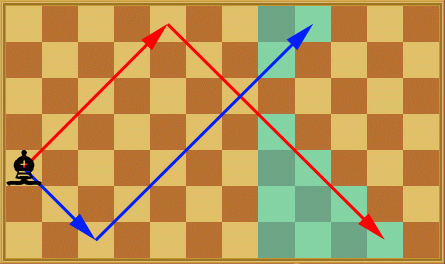



Clearly bishop can visit all the squares of its color left to the column where k-th segments of the polylines intersect. From the part of the board laying to the right of the intersection bishop can visit only squares from the colored triangles. The number of the reachable squares in the described area can be easily calculated by iterating through the x-coordinate till the end of the last segment of the polylines or the end of the border, whatever comes first.

MapFolder

by dgoodman

This problem is hard primarily because the problem domain (paper folding) is unfamiliar. Actually pulling out a piece of paper and folding it helps.

First observe that whenever there are whole columns that have a common map fold direction (all 'u' or all 'd') there cannot be a legal row fold. Second notice that after a fold has been made, the only part of the map that matters for future folding is the bigger of the two areas divided by the fold. So we keep track of the "active" rectangular part of the map. Awe continue to fold, this active region will become smaller and smaller until it is just a single row and column indicating a complete folding of the map.

So the algorithm (using a rotate method to avoid code duplication for rows and columns) becomes

activeRegion = whole map.
ct = foldColumns(activeRegion)  //does column folds sequence, modifying activeRegion
size = area of the activeRegion
while(size>1)
   rotate everything 90 degrees
      ct += foldColumns( activeRegion )
      if(  size == area of activeRegion ) return -1    //NO PROGRESS
      size = area of activeRegion
return ct

So that leaves foldColumns: how to choose a minimum sequence of column folds. No matter what sequence you choose you will finish with the same size active region, but the number of folds required varies. Greedy methods do not work (e.g. always fold nearest the middle). One approach is to do a breath-first search, starting with the entire active Region. Do all legal single folds of that to determine all sub-regions that we can reduce to in one fold. Continue on until we find the first sub-region which allows no further column folding. Then reset the activeRegion to that sub-region and report how many folds were used.

Determining if a fold is legal requires verifying that all the map fold directions on the fold are the same, and that for all the positions in the active region their reflections across the fold have opposite directions. There are a variety of data structures that can be used for the bread-first search, but you cannot afford to allow duplicate sub-regions to propagate or the process can time out.