

| Online Rounds | Room 1 | Room 2 | Room 3 | Wildcard | Finals |
 |
|
 |
|||||||||
|
|
|||||||||||
|
|||||||||||
|
tomek 3-peats! 
by Yarin,
The four top seeds met up in the finals for the ultimate coding showdown. Would it be the methodical Canadian, the excitable Pole, the child prodigy, or the old timer? snewman submitted the easy problem first, proving that he still has what it takes to compete with the young guns. But SnapDragon and reid were right behind, with a spread of only 1.4 points. It was the favorite, tomek who submitted last, coming in four minutes later. All coders than moved on the medium problem, which was quite simple if you saw how to do it. SnapDragon and reid were fastest, taking 9 and 10 minutes, respectively, given the Canuck a 17 point lead.
best = 0
v = empty set
for(H = 32; H < 128; H++) {
w = the set of all cells reached by doing a flood fill from the edges
of the plot, only visiting cells where height is less than or equal to H
for every cell x,y in w that is not also in v
best = max(best, H-plot[x][y]-1)
v = w
}
return best
This algorithm has a running time of O(N^2 * H). RectangleDivision In all counting problems, the first thing to do is to figure out if we can count the number of ways one-by-one, or if we have to use a more clever approach, usually requiring dynamic programming or combinatorics. If the total number of ways can't exceed more than, say, 10 millions, then chances are that you can count them one-by-one. Looking at the input constraints, one have good reasons to suspect that counting the number of ways one-by-one indeed will work, since the maximum size of the rectangle is only 6x6 squares. That makes things a lot easier, because while it is possible to write a dynamic programming solution for this problem, that's a tedious task involving merging components in a row-by-row scan (it would still be a non-polynomial solution, but only in one dimension). So, how do we count the number of divisions? The key is, unlike most grid problems, to focus on the grid edges rather than the grid squares. Imagine the rectangle being a piece of paper and that we simulate a pair of scissors cutting through the paper. We begin at the edge of the paper, and then cut along the grid edges, at each intersection trying all directions. We can start at the top left corner, and then follow the border and try all different edge positions to enter the interior of the paper. If this has been done, and the edge is reached again at some point, we must not continue since this would inevitably cause the paper to be divided into more than two parts (see figure 4). The cutting must also backtrack if a grid intersection that has been reached by the current cutting path is reached again, since this would create a hole in the paper, and such divisions were not to be counted according to the problem description. 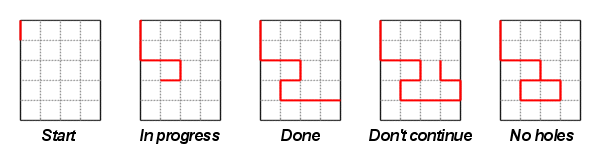 Every time the edge is reached from an interior grid intersection, one division has been found (figure 3 above). To avoid counting everything twice (by a clockwise and counterclockwise cutting), we can force the first cut to go in one specific direction (figure 1). A special case is likely needed when the length of one of the sides is 1, since we then have no interior grid intersection and the algorithm above wouldn't work. However, this was covered by the first example, and shouldn't have tripped any of the coders. And that's pretty much it; the whole solution can be implemented in about 25 lines of code with a recursive function. It might be worth noting that the cutting approach only works when both parts of the division must contain a square on the edge of the rectangle; holes like the one in figure 5 above would otherwise be counted several times. StringOfPowers Another counting problem. This time it's more obvious that we can't do the counting one-by-one, since for the input base=2, digits=18 we have at least 418 different phone numbers made up of only powers of two (containing only the digits 1, 2, 4 and 8). Hence we might start look for a dynamic programming solution right away (or at least a recursive one using memoization). A first simple attempt would be a recursive function with the number of digits left as parameter:
long count(int digitsLeft)
{
if digitsLeft == 0
return 1
long sum = 0
foreach power p of base
if #digits(p) <= digitsLeft
sum += count(digitsLeft - #digits(p))
return sum
}
This simple approach has a serious flaw; it will count some numbers more than once, namely those numbers that can be created in more than one way. The last example in the problem statement had input base=11, digits=2. For this case, the "solution" above would return the wrong answer 2, finding the number "11" in two ways: "1"+"1" and "11". One could try and patch the solution above by ignoring all powers p that are simply concatenations of other powers. This can be done with brute force at the beginning of the program. I won't elaborate on this any further, because while such an approach passes the examples it still doesn't work because of numbers containing the sequence "164" when the base is 2. To solve this problem methodically, we need an approach that is safe. To avoid counting things several times, we must add a single digit at a time, instead of whole sequences of digits. We start at the beginning of the number with the most significant digit, and then recursively try to add new digits, essentially building up a number from front to back, and backtracking on dead ends. For this to work at all, we need to keep a history of the last couple of added digits so we can match a sequence of digits with a power. This history can't contain all the added digits all the time, since the recursive function wouldn't be able to memoize at all (we would then effectively be counting the phone numbers one by one). To handle this, we must also keep track of where in the generated number complete matchings (string of powers) occur. For instance, if the number being built currently is "256168" and the base is 2, complete matching occur after the first, third, forth and fifth digit, since "2", "256", "2561" and "25616" are all strings of powers. We can't throw away the whole digit history as soon as the history matches a power; if we did, the number "2561" for instance wouldn't be found in base 2 because once the first digit, "2" is added, it would be thrown out as it matches the power 2, and the remaining three digits "561" aren't a string of powers. Instead we can only throw out digits in the history when they can't be part of a future power. If the history is "163" (base is 2), this might become the power "16384" later, but if the next digit added is 2, then "16" may be discarded and we only need to keep the history "32". If the next digit instead was 1, we could discard the whole history, because no suffix of "1631" is a prefix of a power of 2 (within 18 digits). So, we have found a way to reduce the history, which means that the input domain to the recursive function has decreased, which enables use to memoize the function. However, we still need to backtrack. If we find that no power can be added from a complete matching location, then we have reached a dead end. For instance, if the history is "6" (again base 2) and there is a complete matching just before this digit (for instance, there is always a complete matching at position 0, the start of the number), it's fine since we could end up with the number 64 or 65536 etc. However, if the next digit added is also a 6 (history becomes "66"), we can backtrack because there is no power of 2 (within 18 digits) starting with 66. There can't be a complete matching between the digits, since the first 6 isn't a power of 2 by itself, and it couldn't be the end of a power of 2 from some digits earlier discarded, because of the way the history is maintained. Maintaining the history and complete matching set in parallel is what solves this problem. Those data structures can be implemented using a simple string (for the history) and a bitmask (for the complete matching locations). Updating them is a bit tricky, but still feasible. Check the reference solution for details. It turns out that the number of positions used in the memoization table is quite small, the judge solution using no more than 56000 positions in the worst case. As a side note, there are actually very few sequences of digits that can be formed in more than one way. Aside from the cases where the base is a sequences of ones, the only numbers that can be formed in more than one way are:
|





|