|
|
||||
| Online Rounds | Room 1 | Room 2 | Room 3 | Wildcard | Finals |
John Dethridge is back in the finals!

by lbackstrom,
TopCoder Member
Thursday, April 15, 2004
So far, the top rated coders have both advanced. In round 3 though, John Dethridge
and ZorbaTHut are rated much closer, and it was anyone's guess as to whether John's
amazingly short code could beat out Zorb's speed, or whether one of the other competitors
would beat the odds and win. Zorb was the first to submit the easy, after 6 minutes. haha
and John were close behind though, with a spread of only 23 points. After half an hour, all
of the competitors had submitted the easy problem, and were working on the medium or
hard problems. However, it proved too much for most, and only John Dethridge was able
to submit it, giving him a brief lead. Zorba wisely game up on the medium problem, and
moved on to the hard, which he had much better luck on. grotmol, having skipped the
medium problem, submitted the hard problem with 6 minutes to spare. At the end of the
coding phase, Zorba was in the lead, grotmol had second, and John was in third. Unless
Zorba's hard problem failed, he was all but assured a victory, and hoped to have the first
upset of the day.
As another uneventful challenge phase wound down, Zorb was guarenteed to at least
advance to the wildcard round, unless both his submissions failed. The scoreboard
started from the last place, showing that all of the competitors with only one submission
passed. Then, we came to John, and saw his solutions both passed. Moving on to
grotmol, we learned that his hard submission failed, giving John a glimmer of hope, and
Zorb a shadow of doubt. As the final results appeared, a red X covered ZorbaTHut's
1K solution, giving John the win.
AutoFix
The easy problem in this round was relatively straightforward. Coders just had to follow the instructions, and most common mistakes were caught by the example cases. The simplest solution starts by tokenizing the input sentence into a sequence of words. Then, it iterates over all adjacent pairs of words, and checks to see if either of the words is absent from the dictionary. If so, then we consider applying the transformation described in the problem statement. First, we must check that the times are within 20 milliseconds. Assuming they are, we then check that both words are in the dictionary after the transformation. The one tricky thing is that, since we are working with words, we need to calculate the index into times for the first character of a word. This isn't particularly hard, but you need to do it in a way that takes into account the fact that you are moving characters around. Here is the pseudocode, where words is the sentence after its been tokenized:
let n = number of words
int idx = lengthof(words0)
for (i = 2 to n)
if (!dictionary.contains(wordsi-1) or !dictionary.contains(wordsi))
if (times[idx+1]-times[idx] <= 20)
s = wordi-1 + wordi.substring(0,1)
t = wordi.substring(1)
if (dictionary.contains(s) and dictionary.contains(t))
wordsi-1 = s
wordsi = t
idx = idx + 1
end
end
end
idx = idx + lengthof(wordsi)
end
ConvexPoly
Since all of the internal angles are 45, 90 or 135 degrees, the convex polygons that we are counting have at most 8 sides. Thus, one approach to counting all of the polygons is to break them into a bunch of different cases depending on the number of sides. However, this would require a ton of code, and would be a lot of work. Instead, we can make a generalization about the nature of the polygons.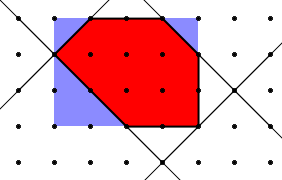
Every convex polygon can be made by starting with a rectangle of some size, and then cutting off some of the corners. The image to the left shows how this works. We start with a rectangle that is 4 wide, and 3 high. Then, we cut off corners of size 0 (which results in no cutting), 1, 1 and 2. In order to avoid double counting any polygons, we are going to only consider cuts that leave the total width and height unchanged. So, for a given width, w, and height, h, we want to know how many valid cuts there are. Clearly, we can not cut more than min(w,h) off any corner without reducing the overall width or height. However, we can cut any amount up to min(w,h) off of a single corner. Furthermore, we can cut off opposite corners independently, since cutting from one corner doesn't reduce the maximum size of a cut on the opposite corner.
Therefore, we can start by writing two nested for loops, one for each of two opposite corners. Once we have cut off the opposite corners, the maximum size of the cut for each of the remaining corners needs to be calculated. If the sizes of the first two cuts (on opposite corners) are i and j, then one of the corners has a maximum cut size of min(h-i,w-j), while the other one has a maximum cut size of min(h-j,w-i). The two cuts can range anywhere from 0 to their maximum value, so we add one to the maximums and multiple them together to get the number of polygons for a given i,j pair. For example, lets say that the first two cuts in the diagram were the upper left and lower right corners. Then, the upper right corner cut has a maximum size of min(3-0,4-1) = 3. The lower left corner cut has a maximum size of min(3-1,4-0) = 2. Therefore, once the first two cuts were made, there were 12 possible pairs of second cuts. The only special case we need to worry about is when we start with a square, and then cut off as much from each opposite corner as we can. This leaves us with a degenerate polygon that is a line. But, by subtracting 2 (for the two diagonals) from the number of polygons we find when looking at a square.
Finally, we have to consider all of the different sizes of rectangles in all of the different positions in the grid. We can do this with 2 more loops that iterate each h,w pair. For a given pair, there are (width-w)*(height-h) different places you can locate the rectangle. So, we end up with 4 nested loops:
long ret = 0;
for(int w = 1; w<width; w++){
for(int h = 1; h<height; h++){
int mul = (width-w)*(height-h);
for(int i = 0; i<=w && i<=h; i++){
for(int j = 0; j<=w && j<=h; j++){
ret += mul*(Math.min(1+w-i,1+h-j) * Math.min(1+w-j,1+h-i));
}
}
if(w==h) ret -= 2 * mul;
}
}
return ret;
Four nested loops like this might be a bit alarming, since each one can go up to 100, and 1004 =
100 million. However, the inner loops don't always require 100 iterations, and it turns out that we execute the
innermost statement about 17 million times, which runs plenty fast. Can anyone improve on the runtime, while
still using constant space -- no lookup tables.
ShortPath
Shortest path on a 2-D grid... just run a breadth first search. That's what a coder might think before he read the constraints. But, with coordinates ranging from -1,000,000,000 to 1,000,000,000, you'll need to do something a bit cleverer. Since there are are at most 50 obstructions, most of the grid is empty, and so most of the shortest path from start to finish will be relatively straight when the start and finish are far apart. This suggests that we build some sort of a graph where we only consider a few points as nodes, and where the edge lengths between nodes are the distances between the points. We will only connect two nodes in this graph if there is a direct, straightforward path between the corresponding points. That is, if there is a path that first goes in one of the four cardinal directions for a while, and then goes in one of the diagonal directions for a while. We can determine if there is such a path between two points by iterating over all of the forbidden points, and checking to see if one of them is in the way. The final question is, what points should we add to the graph?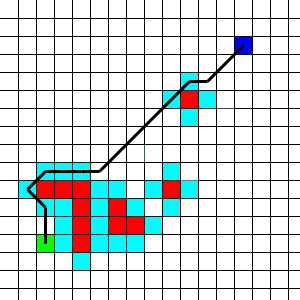
Assuming the shortest path isn't direct, it must pass right next to some forbidden point. If it didn't, we could adjust it a little so that it was either shorter, or did pass right next to some forbidden point. So, we only need to consider points that are adjacent to forbidden points. It turns out that we only need to worry about points that are adjacent to forbidden points in one of the cardinal directions -- not diagonally adjacent. Once we've built this graph, there are at most 200 nodes, and any reasonable shortest path algorithm will give the correct result in plenty of time. For example, the image to the left shows the start in green, the end in blue, the forbidden points in red, and the points that go in the graph in light blue. Notice how the shortest path shown always follows direct paths from one light blue square to another.

