
|
Match Editorial |
Wednesday, August 9, 2006
Match summary
This match had 720 registrants – a little above average, but not as high as one would expect from a money SRM. One reason may have been the schedule, and another could be that the International Olympiad in Informatics takes place in the next week in Mexico and some competitors may be on the way there.
In Division 1 Slovaks did well as misof breezed through the problems, finishing the whole set in 22 minutes and winning the SRM with a comfortable 80 point lead. marian came in second with the help of two challenges of invalid boards in the SillySudoku problem, and zhuzeyuan rounded out the top three.
Division 2 had a easier than usual problem set, with a 900 point problem. Newcomer YuJieLu finished the problems in 12 minutes and had four successful challenges, followed by chenll with two successful challenges. vlad_D, also with two successful challenges, came in third.
The Problems
RosePetals

Used as: Division Two - Level One:
Value 250 Submission Rate 327 / 339 (96.46%) Success Rate 321 / 327 (98.17%) High Score pickley for 249.48 points (1 mins 18 secs) Average Score 237.29 (for 321 correct submissions)
This task is straightforward with no tricky cases. We can just implement a loop over the dice values and add 2 petals to the total count if the value is 3 and 4 petals if the value is 5. This way we get the following solution:
public class RosePetals {
public int getScore(int[] dice) {
int total_petals = 0;
for (int i = 0; i < dice.length; i++) {
if (dice[i] == 3) total_petals += 2;
if (dice[i] == 5) total_petals += 4;
}
return total_petals;
}
}
DigitsSum


Used as: Division Two - Level Two:
Used as: Division One - Level One:
Value 500 Submission Rate 324 / 339 (95.58%) Success Rate 294 / 324 (90.74%) High Score NeoTheOne for 499.42 points (0 mins 58 secs) Average Score 452.28 (for 294 correct submissions)
Value 250 Submission Rate 342 / 342 (100.00%) Success Rate 335 / 342 (97.95%) High Score Revenger for 249.84 points (0 mins 43 secs) Average Score 245.74 (for 335 correct submissions)
This was one of the simplest div 1 tasks of all time, as people solved it in less than a minute. To solve this problem we just code what the problem asks us to. First we need a function to get the sum of digits of a number, and then we need a loop to repeat this until the result is a digit. So here it goes:
public class DigitsSum {
int sumOfDigits(int n) {
int sum = 0;
while (n > 0) {
sum += n % 10;
n /= 10;
}
}
public int lastDigit(int n) {
do {
n = sumOfDigits(n);
} while (n > 10);
return n;
}
}
We can get a shorter solution with the use of some math. Let's use the S(X) notation for the sum of digits of the number X. The following property will be useful: X % 9 = S(X) % 9 (we will prove this later). The result that we need to return is S(S(...S(X)...)), which is the first number smaller than 10. But if X % 9 = S(X) % 9 we have that X % 9 = S(S(...S(X)...)) % 9, so if our result is smaller than 9 then it is equal to X % 9. We are left with the case where X % 9 = 0. If X = 0 then the result is clearly 0. If X is different from 0, we can see that if X > 0 then S(X) > 0 so if X > 0 and X % 9 = 0 then the result in 9. This translates into the following code:
public class DigitsSum {
public int lastDigit1(int n) {
if (n < 10) return n;
if (n % 9 == 0) return 9;
return n % 9;
}
}
vorthys has a one liner based on this ideea.
public class DigitsSum {
public int lastDigit(int n) { return n==0 ? 0 : (int)((n+8L)%9+1); }
}
Kawigi
has a nicer solution, which uses the behavior of % for negative numbers and is language dependent.
public class DigitsSum {
public int lastDigit(int n) { return (n-1)%9 + 1; }
}
Some people who took this approach failed the case when n = 0 or when n was a multiple of 9. Let's prove the property used above: say X = an...a1a0 is a number with digits ai and an is the most significant digit, while a0 is the least significant digit. We can write an...a1a0 = an * 10n + ... + ai * 10i + ... + a1 * 10 + a0.
If we subtract and then add to this number the sum of its digits we get:
an * 10n + ... + ai * 10i + ... + a1 * 10 + a0 - (an + ... + ai + ... + a1 + a0) + (an + ... + ai + ... + a1 + a0) = an * (10n - 1) + ... + ai * (10i - 1) + ... + a1 * (10 - 1) + (an + ... + ai + ... + a1 + a0). Now ( an * (10n - 1) + ... + ai * (10i - 1) + ... + a1 * (10 - 1) ) % 9 = 0
Because (10i - 1) % 9 = 0 (10i - 1 is a number with all digits equal to 9), we get X % 9 = (an + ... + ai + ... + a1 + a0) % 9.


Used as: Division Two - Level Three:
Value 900 Submission Rate 141 / 339 (41.59%) Success Rate 48 / 141 (34.04%) High Score YuJieLu for 866.97 points (5 mins 35 secs) Average Score 552.49 (for 48 correct submissions)
This task is a variation of the classical Josephus problem, as the original problem had m = 2 and asked for the last kid eliminated. The task is an interesting one as it has many different solutions.
Naive solutions which just simulated the game and use a vector or a linked list to keep the kids have timed out. The vector solution times out because deleting an element from a vector takes on average n/2 operations – so we get an algorithm that needs about n * m steps, which is too big to work in two seconds. The linked list solution had a fast deletion but walking around the circle was slow as we needed to do m - 1 steps, so again we have a solution that did about n * m steps.
More efficient solutions follow:
We think of the circle as a line of kids. We ignore the labels of the kids as we are interested only in the kid labeled k. At each step we keep a count of how many kids are left, of how many kids with labels in the set {1, 2, ... k - 1} were eliminated (for this we use the indentifier beforeK), and we also keep the currentIndex, which is the spot where we will eliminate a kid at the current step. It is easy to see that if currentIndex < beforeK + 1. Then we will eliminate a kid with a label smaller than k. Now at each step we update n, beforeK if needed and currentIndex, when currentIndex = beforeK + 1 it means that we are about to delete the kid labeled with k. Here we have some code which does what we just said.
public int kthKid(int n, int m, int k) {
int curIndex = (m - 1 + n) % n + 1;
int beforeK = k - 1;
int nr = 1;
while (curIndex != beforeK + 1) {
if (curIndex < beforeK + 1) {
beforeK--;
}
nr++;
n--;
curIndex = (curIndex - 1 + m + n - 1) % n + 1;
}
return nr;
}
This solution does O(n) steps. For another short solution that took this approach you can check vorthys's solution
or vlad_D's solution,
which has intuitive variable names.
We get another linear time solution not by walking around the circle of kids but moving the circle itself around. First we start counting from the kid labeled 1, and then we need to eliminate the mth kid, and we start again counting from the next kid. We can relabel the circle of kids so that we start again to count for the kid labeled 1 and kids are labeled in a clockwise order, and keeping track at every step of the new label of the kid we are interested in. For example if n = 5, m = 2, and k = 3 at the first step we have the kids labeled: 1 2 3 4 5, when we have to eliminate 2 and get 1 3 4 5 and start counting from 3, by relabeling them we get 4 1 2 3 so the kid labeled 3, was relabeled with 1. Now we must eliminate 3 and start counting again from 4, so relabeling 4 1 2, we get 1 2 3, and the kid we are interested in, who before had the label 1 gets the label 2. Again we eliminate the 3rd kid and relabel, kid 2 gets the same label, then we eliminate 1, and the kid labeled 2 gets the label 1. So now we know that the kid labeled with 3 at the start of the game is eliminated at the 5th step. goldendf's solution implemented in C# is based on this idea. The solution can be easily adapted to finding the last eliminated kid, while the first idea explained above can't be used for that.
In the first two solutions the problem was that we didn't have a efficient data structure that quickly found an element at a specified index (this was a problem for the linked list structure) or couldn't delete an element at a specified index fast enough (this was a problem for the vector structure). A data structure that does both operations quickly can be constructed. One idea would be to split the kids into buckets of size x each, so we would have a total of n/x buckets in total. If we want to find the pth kid in this data structure we can just go over the buckets and find the bucket that contains the pth kid, so knowing the number of kids in each bucket we can find the pth kid bucket in n/x steps, and then for finding the kid in the bucket we need at most x steps. So one eliminating step of our algorithm takes at most n/x + x steps, to minimize this formula we find that x = sqrt(n), so a operation will take O(sqrt(n)) time, thus the algorithm using this data structure will take O(n sqrt(n)) steps in total. chenll took this approach here.
Another data structure that could have worked was a segment tree (explained by misofin the FloatingMedian solution) each node in the segment tree has an associated interval of numbers, and for that interval it keeps count of how many kids in that interval haven't yet been eliminated. Finding the pth kid not deleted yet will take O(log n) steps, and it's very similar to the binary search algorithm. For deleting a kid we need to decrease the count of active kids in all the nodes that have associated intervals which contain the current kid. This step is also O(log n). You can see a solution that works along these lines in whusnoopy's code. The time complexity of this solution is O(n log n).
These two data structure solutions are a bit more complicated than the first two, but using any of them we get the step of the elimination for each kid not for just one specified kid. SillySudoku

Used as: Division One - Level Two:
Value 500 Submission Rate 303 / 342 (88.60%) Success Rate 235 / 303 (77.56%) High Score krijgertje for 482.92 points (5 mins 22 secs) Average Score 323.81 (for 235 correct submissions)
This problem is based on the classical Sudoku puzzle. There is no known polymonial solution for the generalised Sudoku puzzle, so we cannot hope for a solution different from brute force. The original Sudoku puzzle has a table of 9x9 cells, and wikipedia says it has 6670903752021072936960 solution grids, which is why our problem asks about a much smaller table of 4x4 cells. We can suppose that for this table the number of solutions is a lot smaller; this is also suggested by example 4 which had just one cell different from -, and the result of 72, which implies that the number of solutions for a empty table equals 4*72.
There are a lot of different brute force approaches one could take. One would be to try every permutation of 1234 for each row and try to see if it fits with the given table and also see if colums and the four 2x2 squares don't contain each number exactly once. This solution worked in time as it checks only 24 * 24 * 24 * 24 configurations.
Another solution was brute forcing all the solutions with no pruning, and saving the valid configurations as constants. Then when the program was run on a test in the applet it just checked what configurations fit with the input Sudoku table.
A third solution was to use backtraking. We go through cells row by row and on each row from left to right and fill each cell with a value that is still available in the current row, colum and square. See the following code:
int[][] table,r, c, sq;
String[] b;
String[][] sol = new String[288][];
int nr;
public void count(int x, int y) {
if (x == 4) nr++;
else if (y == 4) count(x + 1, 0);
else {
if (b[x].charAt(y) != '-') {
int i = b[x].charAt(y) - '0';
if (r[x][i] == 0 && c[y][i] == 0 && sq[(x/2) * 2 + (y/2)][i] == 0) {
r[x][i] = 1; c[y][i] = 1; sq[(x/2)*2 + (y/2)][i] = 1;
table[x][y] = i;
count(x, y + 1);
r[x][i] = 0; c[y][i] = 0; sq[(x/2)*2 + (y/2)][i] = 0;
}
} else
for (int i = 0; i < 4; i++) {
if (r[x][i] == 0 && c[y][i] == 0 && sq[(x/2) * 2 + (y/2)][i] == 0) {
r[x][i] = 1; c[y][i] = 1; sq[(x/2)*2 + (y/2)][i] = 1;
table[x][y] = i;
count(x, y + 1);
r[x][i] = 0; c[y][i] = 0; sq[(x/2)*2 + (y/2)][i] = 0;
}
}
}
}
public int countWays(String[] board) {
table = new int[4][4];
r = new int[4][4];
c = new int[4][4];
sq = new int[4][4];
this.b = board;
nr = 0;count(0, 0);
return nr;
}
Some people failed the case where all the table was filled and the configuration was valid or invalid.
ThreeMines


Used as: Division One - Level Three:
Value 1000 Submission Rate 54 / 342 (15.79%) Success Rate 40 / 54 (74.07%) High Score misof for 859.77 points (11 mins 52 secs) Average Score 544.00 (for 40 correct submissions)
This problem was a interesting combination of geometry and dynamic programming. misof's solution is one of the most clear solutions, as well as being the fastest submission.
His solution uses memoisation to find memo[r1][c1][r2][c2][cnt], which represents the best profit we can get if we place cnt non-overlapping rectangles in the rectangle defined by corners (r1, c1) and (r2, c2).
The cnt = 1 case is simple and can be solved by either returning the entire rectangle, or returning the best solution from one of the four smaller rectangles that are missing the first row, first column, last row or last column.
In the case where cnt = 2 or 3, we can see that in any configuration of three or two rectangles we can find a horizontal or vertical line that splits the rectangles in two sets. By brute forcing that line we can split the problem in two smaller subproblems on two different rectangles of our original (r1, c1) (r2, c2) rectangle. misof's solution does just that.
There is another trick left unexplained: he uses a B array, where B[x][y] is the sum of the cells (i,j) of the field with 0 <= i < x and 0 <= j < x. Using this array we can quicly compute the sum of the values of the cells in a rectangle with one corner in (r1, c1) and the other corner in (r2, c2) (r1 < r2 and c1 < c2) using the inclusion exclusion principle as being equal to B[r2][c2] - B[r2][c1] - B[r1][c2] + B[r1][c1].
This solution is elegant and very short to write. It's complexity is O(n^5) as we have to fill O(n^4) array values, and for each value to be filled we take roughly O(n) time.
The writer had a O(n^3) solution but it takes a bit more time to code. The solution is based on the fact that there are only 6 possible relative configurations of three non-overlapping rectangles, as we can see in the following picture:
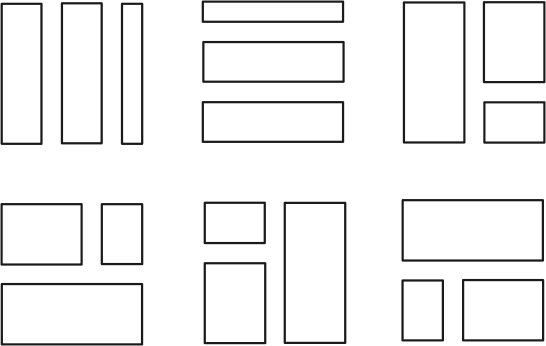
We can brute force in O(n^2) two lines which split the three rectangles in three different zones, and then for each zone we can find the largest square in with a naive solution that tries all rectangles in O(n^4) but we have to use the array B with partial sums. This is just what some people did and succeeded in passing system tests with a solution in O(n^6).
We notice that for a more efficient solution we need the largest sum rectangles in zones of the type: [0..i]x[0..j], [0..i]x[j..m], [i..n]x[0..j], [i..n]x[j..m], [i..j]x[0..m] and [0..n]x[i..j].
We will just explain how to find the best rectangle in a zone of this type: [i..j]x[0..m] the left types can be solved similarly. To find the best rectangle in this zone we must first know the best rectangle in the [i+1..j]x[0..m] zone, and in the [i..j-1]x[0..m] zone. Now we are left to find the best rectangle that has the upper row i and the lower row i. This can be solved in O(n) as we will explain next.
We can think of this subproblem as one that works on finding a maximum sum contignuous subsequence in a linear array A because we have can think to A[k] as the sum of the elements in the rectangle i..j]x[k..k]. Now for finding the best sequence in A, we will use a array sum so that sum[p + 1] = A[p] + A[p - 1] + ... + A[1], now to get the sum of A[p..q] we just compute sum[q + 1] - sum[p]. To get the best subsequence that ends in q, we have to find the smallest sum[p] so that sum[q + 1] - sum[p] is maximum. This idea translates to the folowing code:
int[] sum = new int[A.length + 1]
int best = - infinity;
sum[0] = 0;
for (int i = 0; i < A.length; i++) sum[i + 1] = A[i] + sum[i];
int mins = 0;
for (int i = 0; i < A.length; i++) {
if (best < sum[i + 1] - mins) best = sum[i + 1] - mins;
if (mins > sum[i + 1]) mins = sum[i + 1];
}
return best;
We have O(n^2) regions in our algorithm and as we shown above each region can be solved in O(n), thus we have a O(n^3) time algorithm.
