 |
 |
| Reception | Room 1 | Room 2 | Room 3 | Room 4 | Final Round | Slide Show |
Play-by-Play | Photos | Problem Analysis
Problem Set Analysis & Opinion

by schveiguy,
TopCoder Member
Thursday, December 4, 2003
T9Input
Used as: Division 1 - Level 1:
Most newer cell phones allow text messaging so you can "text" your friends with the latest gossip. This problem turns your pc into an "english-to-cellphone" translator. The problem at hand is very straightforward, with two steps. First, build the dictionary, then translate the words.
The dictionary can be built by creating an array of all the words typed in the message. For each word, figure out its numeric sequence by replacing each letter with the appropriate number from the mapping given in the problem. Each language has a map object which can map a string to another object. In this case, we map the numeric sequence to a set of strings. The set will have only unique strings in it, and will be alphabetically sorted.
For the second step, move through all the messages, replacing with the appropriate numeric sequence for each word. Using the same method to figure out the sequence, look up each word in the dictionary. If there is more than one word with the same sequence, the set at the appropriate map location will have more than one element. Since the set is already sorted, the number of 0's to add depends on what index contains the current word. If the index is i, we add i 0's to the output. For spaces we simply add a pound sign '#'.
ImmutableTrees
Used as: Division 1 - Level 2:
While one might hope for a short, simple solution to this problem that doesn't require constructing any trees, it turns out that the simplest solution by far involves writing an Immutable Tree class. Binary trees are pretty standard fare, especially at this level of competition, but the immutable aspect requires a slight tweak to the standard insert method. Normally, the insert method would look something like this:
class BinaryTree{
int value;
BinaryTree left, right;
void insert(int v){
if(v<value){//go left
if(left == null)left = new BinaryTree(v);
else left.insert(v);
} else {
if(right == null)right = new BinaryTree(v);
else right.insert(v);
}
}
...
}
However, this method clearly changes the original tree, so we want to modify it to leave the original tree alone, and have it return the modified tree. The first change is to update the method signature so it returns a tree, and then make a couple more changes so that the parts of the tree that stay the same get reused:
class BinaryTree{
int value;
BinaryTree left, right;
BinaryTree insert(int a) {
BinaryTree ret = new BinaryTree (v);
ret.right = right;
ret.left = left;
if(v<value) {
if(ret.left==null)ret.left = new Tree(v);
else ret.left = ret.left.insert(v);
} else {
if(ret.right==null)ret.right = new Tree(v);
else ret.right = ret.right.insert(v);
}
return ret;
}
...
}
That's pretty much it. After we have the tree class written, its just a little bookkeeping to keep track of which nodes are garbage.
NCushion
Used as: Division 1 - Level 3:
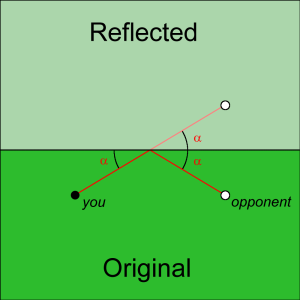
This problem asks you to find directions you can shoot a billiard ball such that it bounces off of a certain number of cushions, and then hits a second ball. Many geometry problems involve transforming the search space of the problem to be simpler, and this is no exception. At first glance, it seems that some sort of search using angles may be required. However, if we just transform how bounces occur, we can make each shot a single straight line. We can use some common sense to show how it works. When you look into a mirror at an object, you are essentially seeing the object "inside" the mirror, but in a reversed fashion. The object of course isn't actually inside the mirror, the light reflecting off the object is entering our eye after reflecting off the mirror. Your brain is performing the transformation of "seeing" the object inside the mirror. We must do the same thing with the cue balls.
We see in the diagram from the problem that the path of the ball leaves at the same angle of incidence as it went in with. What we can do is flip the pool table along the cushion so that it is reflected as if the cushion was a mirror. The opponent's cue is also reflected. We see from the diagram below, that the ball's initial path combined with its reflected path is a straight line:
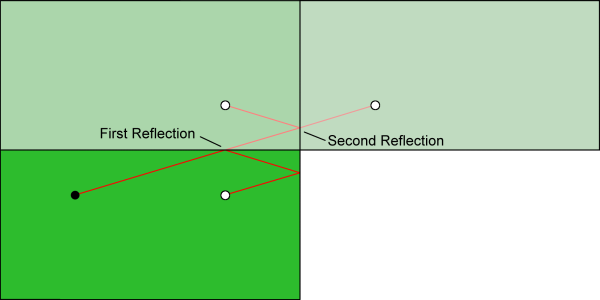
This is true no matter how many cushions we go through. Each time we go through a horizontal cushion, the table flips over vertically, and each time we go through a vertical cushion, the table flips over horizontally:
This gives us an easy way to determine the angle for hitting a ball with N cushions. Note that there is only one way to hit a ball such that it hits a particular sequence of cushions and hits the other ball. Any other angle, and it would miss the ball. Therefore, there is one shot per sequence of cushions. In addition, some sequences of cushions are invalid. For example, it is not possible to hit the ball so it hits 5 horizontal cushions and then 5 vertical cushions to get 10 cushions. It turns out, that there is only one way to hit the ball so it hits i vertical cushions and j horizontal cushions and then the opponent's ball. Therefore, we can determine very quickly the angle to hit the ball at so that it hits the opponent's ball reflected in i vertical cushions and j horizontal cushions. The reflected tables form a diamond, as shown below with a sample diagram for N = 2 cushions:
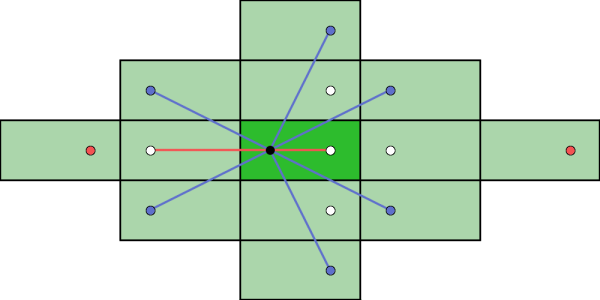
In this diagram, the black ball represents your ball, the white balls represent balls that if hit would be less than 2 cushions, the blue balls represent balls that can be hit going through 2 cushions, and the red balls represent balls that cannot be hit because they are blocked. Notice how each valid shot crosses exactly two cushions, whereas the shots which are blocked do not. We can see from the diagram that the maximum number of ways to hit the ball is equivalent to the number of integer solutions for i and j in the equation:
|i| + |j| = N
However, we must take into account that the ball could hit the opposite ball before hitting N cushions. In this case, we need to remove all these shots. But how do we find these? Since the search space is at most a 1000x1000 grid, we can simply iterate over all the ways to hit less than N cushions and compare the shots. We can achieve a canonical form of a shot by taking the x and y difference, and forming a vector. Then we can take the GCD of the two and divide to create a reduced form of the vector. If we store in a set the reduced vectors required to hit the ball in N cushions, we can then iterate through all the ways to hit the ball in less than N cushions and remove vectors from our set which match. In fact, this is how the writer's solution is formed.
The above solution works, but it is not the most efficient method. A more efficient method is to take the vector of each shot, and find out if there are any shots which have the same vector. To find shots which have the same vector, we loop through all the x grid points and find the x locations of the ball at each grid point. If the x delta is a multiple of the x component of the vector, then figure out what the y delta is for the vector. If a ball exists at this coordinate, you can remove the shot in question. We can answer this question by determining how many horizontal cushions have been passed through, and then figuring out what the y coordinate of the ball should be. There is a special case when the x-component of the vector is zero. In this case, the opponent's ball will always interfere when N > 1, and will interfere when N = 1 and your cue must go through the ball before hitting the first cushion.
This method is more efficient because it does not even consider shots which are not on the vector lines, it also can break out of the loop after removing a shot, and it does not need to store the shots in a set. For an example of this method, see my solution in the practice room (I'll put it up sometime today or tomorrow).
