ACRush wins Room 2!

Discuss this match
Wednesday, October 31, 2007
Introduction by Olexiy

The highest rated TopCoder member ACRush had plenty of strong opponents in Semi 2 - cyfra and gawry (two former 3000+ coders), darnley and Per (both at the top of their form) and the third highest rated coder marek.cygan (he is also the highest rated polish coder, the title worth many others). Nevertheless, the rating favorite cruised through the packed field with correct solutions for all 3 problems and an impressive win. gawry came second with only a slight lead over third-placed Per. marek.cygan, cyfra and sghao126 rounded the top 6 and extended their title campaign for at least one more day. Good luck to all advancers and hope they'll succeed in the Incredible Race as well!
SongsList
Let's fix one of 6 possible formats for the song 0 and determine all possible positions of this song, written in this particular format, in the sorted list. To do this, we divide all the other songs into 3 categories:
- The songs, which come before song 0 lexicographically in any of 6 possible formats.
- The songs, which come after song 0 lexicographically in any of 6 possible formats.
- All the songs, not included into the previous 2 categories.
Let C1, C2 and C3 be the number of songs in each of 3 categories, correspondingly, and N be the total number of songs (including song 0). It's easy to see, that we can't put song 0 into positions 0, 1, ..., C1-1 in the sorted list, because C1 songs from category 1 are always lexicographically smaller than song 0. Similarly, we can't put song 0 into positions N-C2, N-C2+1, ..., N-1, because C2 songs from category 2 are always lexicographically larger than song 0. But what about positions �1, C1+1, ..., N-C2-1? We can put song 0 into each of these positions. To put it into position X, C1 ≤ X < N-C2, we need to write X-C1 songs from category 3 in such way, that they are lexicographically smaller than song 0, and all the other songs from category 3 in such way, that they are lexicographically larger than song 0.
We've described all the possible positions of song 0, written in one particular format, in the sorted list. To obtain the answer, we just need to repeat this procedure for all 6 formats of song 0 and return the union of all available positions.
FlashFlood
The solution of this problem consists of two parts. In the first part, we break the relief into parts (we call this parts "basins"), using the following algorithm. To find the first basin, we start from the town and draw the horizontal ray to the left until it crosses the relief. The part above the relief and under the ray forms the first basin. To find the second basin, we start from the end of the first one and climb to the left until we reach the local peak. Then we again draw the horizontal ray to the left and form the second basin. The process is repeated to form more basins and terminated when the ray doesn't cross the relief. The picture below illustrates the process:
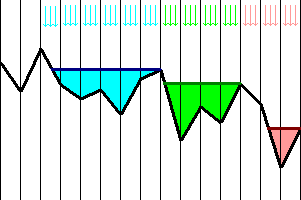
Each basin is drawn by its own color - red, green or blue. Each basin has the area (flooded in the picture) and the speed of rain (shown using the arrows of basin's color). As only rain fills all the area of the basin, it's become overflooded. Obviously, water starts flooding the town exactly, when the rightmost basin will become overflooded.
Now comes the second part of the solution, in which we just simulate the process. In this part, we calculate for each basin the time, needed to overflood it (this time is basin's free area, divided by basin's rain speed), and choose the basin, which will be overflooded first. If it's the rightmost basin, then the process is finished. Otherwise, the water from the overflooded basin will become flow to the basin immediately to the right. Now, from our point of view, the overflooded basin and the basin immediately to the right can be treated as one larger basin. The area, the filled area and the speed of rain in this new basin equal to the sum of areas, filled areas and rain speeds in two old basins. We replace two old basins by the new one and continue simulation. The described procedure is repeated until the rightmost basin will be overflooded.
ReliefMeasuring
Let's call a map correct, if it might be accurate, and incorrect otherwise. First we establish some properties of correct maps.
Basic criteria. A map is correct with peak at cell (R, C) if and only if there are no two neighbouring cells A and B such, that A is a 1-cell, B is a 0-cell and B is closer to the peak than A.
Proof. If there are such two cells A and B, then A's height is greater than some constant value, and B's height is not, so A's height is greater than B's height. It means, that the map doesn't satisfy to the property from the problem statement, i.e. it is incorrect. From the other hand, if there are no such two cells A and B, then we can assign height 1 to each 1-cell and height 0 to each 0-cell. This assignment satisfies to the property from the problem statement, so the map is correct. End of proof.
Now let's find some deeper properties of correct maps with peak at cell (R, C). It's easy to see that the map, containing only 0-cells, is correct. As this case is easy to check, we'll consider only maps, containing at least one 1-cell. Let LC be the index of the leftmost column of the map, containing at least one 1-cell, and RC be the index of the rightmost such column.
Property 1. LC ≤ C ≤ RC. Each column c, LC ≤ c ≤ RC, contains at least one 1-cell.
Proof. Let (r1, LC) be any 1-cell in LC-th column of the map and (r2, RC) be any 1-cell in RC-th column of the map. If LC > C, then pair of cells A=(r1, LC), B=(r1, C) won't satisfy to the basic criteria. If RC < C then pair of cells A=(r2, RC), B=(r2, C) won't satisfy to the basic criteria. If some column c, LC < c ≤ C, doesn't contain 1-cells, then pair of cells A=(r1, LC), B=(r1, c) won't satisfy to the basic criteria. At last, if some column c, C ≤ c < RC, doesn't contain 1-cells, then pair of cells A=(r2, RC), B=(r2, c) won't satisfy to the basic criteria. End of proof.
According to the property 1, for each column c, LC ≤ c ≤ RC, there are numbers stc - the row index of the topmost 1-cell in the column c, and fnc - the row index of the bottommost 1-cell in the column c. The following two properties can be proven in the similar way, as it was done while proving the property 1 (i.e. we suppose the property doesn't hold and find the pair of cells which doesn't satisfy to the basic criteria), so their proof is left to readers.
Property 2. For each column c, LC ≤ c ≤ RC, and each row index r, stc ≤ r ≤ fnc, the cell (r, c) will be the 1-cell.
Property 3. The following inequalities will hold:
- stLC ≥ stLC+1 ≥ ... ≥ stC-1 ≥ stC ≤ stC+1 ≤ ... ≤ stRC-1 ≤ stRC;
- fnLC ≤ fnLC+1 ≤ ... ≤ fnC-1 ≤ fnC ≥ fnC+1 ≥ ... ≥ fnRC-1 ≥ fnRC;
- stc ≤ R ≤ fnc, for every c, LC ≤ c ≤ RC.
It can be proven, that if map satisfies to all 3 established properties, it will also satisfy to the basic criteria, so correct maps are exactly those maps, which satisfy to all 3 properties. This fact allows us to solve the problem using dynamic programming. As we can brute force all possible values of R, let's suppose for the next paragraphs, that the value of R is fixed.
Note, that every map can be broken into two parts - the left part consists of columns between 0 and C, inclusive, and the right part consists of columns between C+1 and last, inclusive. Let F(i, j, k) be the minimal number of characters, we need to replace in the columns of map between 0 and i, inclusive, in such way, that these columns will form the left part of a correct map with C=i, stC=j and fnC=k.
To calculate F(i, j, k), we use dynamic programming. It is possible that LC=i, in this case we need to change all cells in columns between 0 and i-1, inclusive, to 0-cells. It is also possible that LC<i, in this case we can iterate through all possible values of sti-1 and fni-1, sti ≤ sti-1 ≤ R ≤ fni-1 ≤ fni, and try to add i-th column to the best possible left part for the columns between 0 and i-1, inclusive (it's cost is F(i-1, sti-1, fni-1)). Among all possible cases we choose the best one.
Let G(i, j, k) be the minimal number of characters, we need to replace in the columns of map between i+1 and last, inclusive, in such way, that these columns will form the right part of a correct map with C=i, stC=j and fnC=k. Note, that G-values can be calculated using dynamic programming in a similar way as it was done when calculating F-values.
Now, when we have F and G, it's easy to get the answer. We need to iterate through all possible values of C, stC and fnC, and note, that if C, stC and fnC are fixed, then the minimal number of changes for the correct map is obtained by gluing the best corresponding left and right parts together, i.e. this number equals to F(C, stC, fnC) + G(C, stC, fnC).