



 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
||||||||
 | ||||||||||
|
||||||||||
|
||||||||||
|
mathijs wins Room 2
OlympicsBroadcastingby soul-netThis problem was a generalization of the classical problem that asks for knowing whether a set of intervals cover a (bigger) interval. The solution can be actually derived from one known solution for that problem. If we graphically see the intervals as segments, we can see that each interval of the form [n,n+1] is covered by some number of segments. You can easily see that number is an upper bound on the number of total channels. For example, here is the picture representing the set of intervals { [0,3],[1,5],[2,4],[4,6],[0,6] } over the universe [0,6]. Below the integer coordinates is the number of segments that cover that length 1 interval. We'll call this numbers the height of the interval. 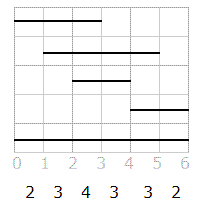
In this example, the upper bound is 2. Is this upper bound achievable? It is, actually. By shrinking the segments that go through intervals with height greater than the minimum (in the original statement this can be seen as banning out parts of events, which is allowed) you can always get all heights to be exactly 2. 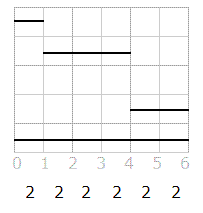
In this case, note that some intervals may be completely shrunk and disappear. If heights are all exactly the same (let's call it h), it means that whenever a segment terminates, another one exactly starts at that point. Simply merging those two and repeating the operation will lead to exactly h intervals that cover the entire universe, and they represent one way to assign the channels that achieve the upper bound. Finally, since we have an always achievable upper bound, all that is needed is to find that number and return it. Calculate the height in each [n,n+1] interval is not possible because there can be too many of them, but note that the height only changes when a segment starts or ends (is increased or decreased by one, respectively), and there are at most 100 of those points (2 for each segment). Therefore, we can just calculate all heights and keep the minimum by iterating those points. C++ code follows (for non C++ coders, note that map represents a dictionary that iterates the keys in sorted order):
map<int,int> m; //by default, all keys have value 0
for(int i=0;i<from.size();++i) m[from[i]]++, m[to[i]]--; //calculate height different at each point
if (m[0]==0) return 0;
int h=0,hs=100000;
for(map<int,int>::iterator it=m.begin(); it != m.end() ; ++it)
h+=it->second; //add height difference at this point
if (it->first<totalUnits) hs=min(hs,h); //if we are before the end, update the minimum
}
return hs;
DominoesFindingby soul-netBacktracking. Yes, that's it. Knowing that a problem is in fact solvable with a backtracking approach is most times a matter of intuition gained with experience. Anyway, in this and some other cases, there can be found more formal estimators that the idea is in fact THE idea. I'll describe a possible backtracking approach, possibly the easiest to implement, but there are other possibilities. The idea is based on the fact that all squares must be used. For example, if we take the upper-left square of the board, we can see that we must connect it with one of its two neighbors. With this in mind, we can iterate over all squares and, each time we find an unused one, we know that we must match it with one of its two (or one) remaining neighboors -- or both, if we iterate in a column-row or a row-column fashion; when we find an unused square, we know that everybody in its upper-left rectangle is already used. As we do this, we go marking each used piece and only continue trying if the new piece made by each new matching is "new". In this way, if we finally get all squares to be used, we know also that all pieces are used (because we managed to get no repeats) and then, we add 1 to the counter. To be sure this approach works perfectly in time, you can conduct a little experiment and run the algorithm over an empty board without the "new piece" pruning. This will show you that there are less than 1.3 million ways to divide the board (1,292,697 actually), so it is perfectly feasible to try every one of them. Of course, the pruning of the "new piece" will reduce the running time dramatically in most cases. There is also a good theoretical estimator that the approach will work in time, to convince ourselves before programming anything (many programmers think this is a must). There is a total of 56 squares in the board, our algorithm does nothing for half of them (when it finds them already used) and tries 2 or less cases for the other half (the ones it finds unused). This means the total number of leaves in the search tree will be bounded by 256/2 which is roughly 256 millions. This is pretty big, but considering it is a wide margin upper bound, it can be pretty well used as a "proof" that time limits won't bother. Main part of a Java code follows:
void spi(int a, int b, boolean st) {
pi[a][b]=pi[b][a]=st;
}
int count(int i, int j) {
if (j==7) {i++;j=0;}
if (i==8) return 1;
if (oc[i][j]) return go(i,j+1);
int r=0;
if (!oc[i][j+1] && !pi[b[i][j]][b[i][j+1]]) {
spi(b[i][j],b[i][j+1],true);
oc[i][j+1]=oc[i][j]=true;
r+=go(i,j+2);
oc[i][j+1]=oc[i][j]=false;
spi(b[i][j],b[i][j+1],false);
}
if (!oc[i+1][j] && !pi[b[i][j]][b[i+1][j]]) {
spi(b[i][j],b[i+1][j],true);
oc[i+1][j]=oc[i][j]=true;
r+=go(i,j+1);
oc[i+1][j]=oc[i][j]=false;
spi(b[i][j],b[i+1][j],false);
}
return r;
}
FastGossipby soul-netNoting the low upper bound of the number n of nodes of the graph, probably many finalists immediately started thinking of an exponential idea. The fact that the running time of the problem was an exponential with base 3 instead of the usual 2 made coming up with it a little more complicated. Each individual can be in one of 3 states at each moment:
The initial state is of course the individual 0 in state (2) and the rest in state (0). Now, let's add an edge of weight 0 for every possible communication, which means, from state s all ways of selecting a friend i in state 2 and another one j in state 0 such that i is willing to call j and "make them talk" by pointing the edge to a state that has everybody in the same state as in s, except for i and j that will be in state (1). Also, let's add an edge of weight 1 from each state s that has at least one friend on state (1) to another state in which all individuals in state (2) are given state (1). This edge represents the minute passing. All that's left is to run a bifid BFS or a bounded edge dijkstra algorithm on the graph and return the minimum path to the final state (which is, of course, the state with all friends in state (2)). Problem: The graph may have almost 5 million nodes and from each node there can be up to 14*14 edges. To make the algorithm run on time with 14*14*5*106 nodes you must do a lot of somehow low level prunning. But of course, there is a much better solution. Instead of adding edges of weight 0 for making any pair talk, only add edges for a fixed friend i and all possible j's. Since the order in which you make the pairing (i.e., tranverse the edges of weight 0) is not important, whenever friend i calls somebody, this simplification is still optimal. The only missing possibility is that at some minute friend i must call nobody (probably because everybody he is willing to call is already aware of the news). To contemplate that case, we add an edge of weight 0 from state s to the state in which i is in state (1) and all the rest are unchanged. This "being on the phone with himself" represent that he is not going to actually use the phone this minute. This new graph has approximately 14*5*106 which is a 1/14 improvement from the previous graph and can fit in time without any kind of low level optimizations. |
    |