
|
Match Editorial |
Qualification Round Problem Sets
February 28 - March 1, 2006
Match summary
PScores
Being probably the most straightforward among the qualifiers, this problem required a very accurate implementation. So, to find the answer we must iterate through all possible p-values and accurately simulate the process for each of them. If the score for some value is equal to the input score, increment the answer counter:
public int howMany(int[] nexts, int score){
int ret = 0;
for(int i = 0; i < nexts.length; i++){
int ii = i;
boolean[] visit = new boolean[nexts.length];
visit[ii] = true;
while (!visit[nexts[ii]]) {
ii = nexts[ii];
visit[ii] = true;
}
if (ii == score) ret++;
}
return ret;
}
SlowKeyboard
The main part of this problem is to estimate how long it will take to type some number. If one needs to type "MMSS" number, the total time will be 4 + 2 secs for each pair of non-equal consecutive digits:
int needTime(int m, int s){
int ret = 4;
if (m % 10 != m / 10) ret +=2;
if (s / 10 != m % 10) ret +=2;
if (s % 10 != s / 10) ret +=2;
return ret;
}
Having that computed, the easiest way to solve the whole problem is the following. Use a loop increasing the time by 1 second per iteration. At each iteration, check whether we were able to finish typing in time:
int m = Integer.parseInt(time.substring(0, 2));
int s = Integer.parseInt(time.substring(3));
int tm = 0;
while(true){
if (t(m, s) <= tm) return tm;
tm++;
s++;
m += s / 60;
s %= 60;
m %= 60;
}
Another way is to bruteforce over all 3600 combinations of minutes and seconds, choosing the best one.
Runway
Since patches have integer endpoints, we can represent each patch as a set of integer intervals of length 1 (for example, patch [1, 4] can be represented as [1, 2] + [2, 3] + [3, 4]). A patch needs to be inspected if there exists at least one sub-interval with integer coordinates, which is not covered by later patches. To solve the problem, just iterate over all patches, split each of them into subintervals of length 1 and check each of those subintervals:
int inspect(int[] x0, int[] x1) {
int ans = 0;
for (int i = 0; i < x0.length; i++) {
boolean inspect = false;
for (int j = x0[i]; j < x1[i] && !inspect; j++) {
boolean ok = true;
for (int k = i + 1; k < x0.length && ok; k++)
ok &= (x0[k] <= j && x1[k] > j);
inspect |= ok;
}
if (inspect) ans ++;
}
return ans;
}
BankingArray
To solve this problem you just need to strictly follow instructions given in the statement:
Java implemenation of the algorithm follows:
public int addCost(int T, int N) {
int size = 0;
int ans = 0;
while (true) {
int v = Math.min(N, T - size);
ans += v;
N -= v;
if (N == 0) return ans;
size = T;
ans += T;
T *= 2;
}
}
FractionCounting
We need to count all fractions of the form (p / q), where w <= p <= x and y <= q <= z. Both x and z are not greater than 100, so we can brute force over all acceptable p and q. The difficult thing here is to assure we don't add the same fraction more than once (for example, 2/2 and 4/4 are the same). Therefore we need to mark each fraction we counted. The natural way to do that is to deduce the fraction dividing both numerator and denominator by their greatest common dividor (GCD).
First, we need to write a function to compute the GCD of two numbers. Because of low constraints this can be brute forced, but the most common implementation is much faster:
int GCD(int a, int b) {
return (b == 0) ? a : GCD(b, a % b);
}
As soon as we have this, we just maintain a 2-d array remembering the deduced form for each fraction we can construct (C++ code follows):
int howMany(int w, int x, int y, int z) {
vector<vector<bool> > visit(x + 1, vector<bool>(z + 1, false));
for (int i = w; i <= x; i++)
for (int j = y; j <= z; j++)
visit[i / GCD(i, j)][j / GCD(i, j)] = true;
int cnt = 0;
for (int i = 0; i <= x; i++)
cnt = accumulate(visit[i].begin(), visit[i].end(), cnt);
return cnt;
}
MaxKTrace
If our Dynamic Programming tutorial had been written earlier, it definitely would have included this problem as an example. As the tutorial says, DP is used when "a sub-solution of the problem is constructed from previously found ones.". In our problem, you can build a submatrix of size K by choosing the first row and the first column of this submatrix and attaching them to a (K-1)-submatrix (and, similarly, build the optimal K-subtrace using optimal (K - 1)-subtrace).
The very first step when solving a DP-memo problem is to find how to define a state which represents a sub-problem. Since we are going to solve our problem splitting the submatrix into first element of the trace and a smaller submatrix, the state must contain the size of the submatrix we are looking for. Also, all rows and all columns of the smaller submatrix must be located below and to the right of the first element, respectively. To ensure this, the state will contain the indeces of the first row and the first column which can be used building the submatrix.
The next step is to find a state for which an optimal solution is found. In our problem, we know that optimal 0-trace is always equal to 0. The only thing left is to find how K-subtrace is dependent on (K-1)-subtraces. So, if we are looking for the optimal K-subtrace, r and c are the indeces of the first row and column we can use, respectively, then we have 3 choices:We've explained a memoization algorithm, a similar DP implementation follows:
public int getLargest(String[] mat, int K){
int[][][] max = new int[mat.length][mat[0].length()][K+1];
int ret = 0;
for(int i = 0; i < max.length; i++)
for(int j = 0; j < max[0].length; j++) {
Arrays.fill(max[i][j], -1000000);
max[i][j][0] = 0;
}
for(int i = 0; i < max.length; i++){
for(int j = 0; j < max[0].length; j++){
max[i][j][1] = mat[i].charAt(j) - '0';
for(int k = 1; k < max[0][0].length; k++){
if (i > 0) max[i][j][k] = Math.max(max[i-1][j][k], max[i][j][k]);
if (j > 0) max[i][j][k] = Math.max(max[i][j-1][k], max[i][j][k]);
if (i > 0 && j > 0) max[i][j][k] = Math.max(max[i][j][k], max[i-1][j-1][k-1] + (mat[i].charAt(j) - '0'));
}
ret = Math.max(ret, max[i][j][K]);
}
}
return ret;
}
DigitFiller
Here coders faced another almost-textbook DP problem. The problem asks us to check all the numbers which match the given mask and count those who are divided by num.
If number is X written as "A0A1...Ak" in decimal, then the following is true:
X % num = (A0*10k - 1 + A1*10k - 2 + ... + Ak*100) % num
= (A0*10k - 1) % num + (A1*10k - 2) % num + ... + (Ak*100) % num.
If so, we can consider digits independently from left to right.
At each place, we will try to substitute an 'X' with each of 10 digits, store the remainder left after this digit, and continue to the next one.
These data - number of digits processed and the remainder left - is a
state which we will use in our
DP solution.
Now we need to find other 2 requisites - the state when the answer can be determined directly and how to move from one state to another.
The first can be found easily. If we've passed all digits already, then the answer is either 1 if the remainder is 0 (so the number we built can be divided by num) or 0 otherwise. Moving between states isn't extremely hard too. If the input number has a digit at some place, we just multiply the digit by a corresponding power of 10, take modulo num, add the result to the remainder we had and continue to the next position. If the input number has a 'X', we perform the same procedure for all possible digits between 0 and 9. The core function of a memo solution follows:
long numCases(int where, int left) {
if (where == N) return (left == 0) ? 1 : 0;
if (memo[where][left] != -1) return memo[where][left];
int mm = dd[N - 1 - where];
if (data.charAt(where) != 'X')
return memo[where][left] = numCases(where + 1, (left + (int)(data.charAt(where) - '0') * mm) % num);
long res = 0;
for (int i = 0; i < 10; i++)
res += numCases(where + 1, (left + mm * i) % num);
return memo[where][left] = res;
}
NumJordanForms
To return the total number of Jordan forms one needs to find the number of partitions for each element of charPoly, and then multiply all these numbers. Since numbers can grow really huge, we perform all operations modulo 179424673 (which is the 10M-th prime number). Now we'll concentrate on finding the total number of partitions for charPoly[i].
We need to find the number of ways to split the number A into several positive numbers (components), such that the sum of the components is equal to A, all components are not greater than number B and at least one component is equal to B. Lets solve a simpler problem first - forget about the last constraint and allow all components be strictly smaller than B. This is a classical DP / memoization problem, which can be solved in A*B space and time:
int[][] memo;
int numWays(int A, int B) {
if (A < 0) return 0;
if (A == 0) return 1;
if (B <= 0) return 0;
if (memo[A][B] != -1) return memo[A][B];
int ans = GV(A - B, B) + GV(A, B - 1);
return memo[A][B] = (int)(ans % 179424673);
}
Here, we take components in non-increasing order. So, to split the number A, we can either have one component to
be equal to B and solve the problem for (A - B, B),
or don't take any component equal to B and continue to the smaller components - (A, B - 1).
To get the answer, sum these 2 values and take modulo 179424673.
Now we need to incorporate the last constraint into the statement. This is rather easy - to ensure that at least one component of the partition will be equal to minPoly[i], we will subtract minPoly[i] at the very beginning (making it the first component) and continue with numWays method:
public int howMany(int[] charPoly, int[] minPoly) {
long ans = 1;
for (int i = 0; i < charPoly.length; i++) {
ans *= GV(charPoly[i] - minPoly[i], minPoly[i]);
ans %= M;
}
return (int)ans;
}
BigFibonacci
The i-th Fibonacci number can be easily found in linear time: just keep adding Fi - 1 and Fi to get Fi + 1 until you are done. But for the possible inputs for this problem, the linear algorithm is too slow - we don't have enough time to perform 1015 iterations. Lets look at Fibonacci sequence from another point of view. Since each Fibonacci number depends only on 2 previous numbers, its natural to keep only these 2 last numbers. Switching from pair (Fi - 1, Fi) to pair (Fi, Fi + 1) can be described as a transformation matrix A:
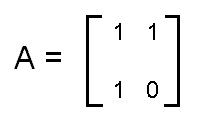
In other words, (Fi + 1, Fi) = A * (Fi, Fi - 1). As you can easily prove, if B = Ak, then B[0][0] = Fk + 1, B[0][1] = B[1][0] = Fk and B[1][1] = Fk - 1. Having that found, you just need to power the matrix in logarithmical time. This powering can be simplified even more by using the dependencies between elements of the matrix.
This thread proposes some other methods to solve the problem.
Synchro
The scores on this problem were the lowest among all the qualifiers, though the code itself isn't too long. First, lets change the "coordinate system" a bit. Instead of computing everything related to the immovable clock, lets make the slowest hand immovable and transform hands to compute their position relative to it. With that transform applied, the slowest hand will always point at 12 hours and speeds of all other hands will be equal to the difference between their original speeds and the speed of the slowest hand (so, if watch = {2, 3, 17}, then new speeds will be {0, 1, 15}). Here, all hands can agree only when they point at 12 hours mark (because the slowest hand now always point there). If new hands speeds are s0, ..., sk - 1, then hands will need 60 / s0, ... , 60 / sk - 1 minutes respectively to pass an hour. In other words, the second hand will be at 12 hours every 60 / s0 minutes and the (k - 1)th hand will be at 12 hours every 60 / sk - 1 minutes. Therefore, they will be at 12 hours every 60 / s0, 60 / s1, .., 60 / sk - 1 hours, and all of them will again point at 12 hours in 60 / GCD(s0, s1, .., sk - 1) hours. Having that computed, we use the speed of the slowest hand to find the minute position. Java code follows (don't forget about a special case when all hands are of the same speed):
public double resynch(int[] watch){
int[] dif = new int[watch.length-1];
int g=0;
for(int i = 1; i < watch.length; i++){
dif[i-1]=Math.abs(watch[i]-watch[i-1]);
if(dif[i-1]!=0) g=dif[i-1];
}
if (g == 0) return 0.0;
for(int i = 0; i < dif.length; i++) g = gcd(g, dif[i]);
double hr = 60.0 / g;
double rev = hr * watch[0] / 60;
rev = rev - (int)rev;
return 60.0*rev;
}
