
|
Match Editorial |
Online Round 1-A
September 21, 2006
Match summary
Petr and ACRush turned the first round of the TCCC into a close race. ACRush won the coding phase with 1180 points, against Petr's 1150, and won the challenge phase with 100 points against Petr's 75, securing the top spot and passing the 3000+ rating mark. He is only the 19th coder in TopCoder history to reach this milestone.
The Problems
StringSquares

Used as: Division One - Level One:
Value 250 Submission Rate 431 / 465 (92.69%) Success Rate 393 / 431 (91.18%) High Score qiangfu for 249.33 points (1 mins 28 secs) Average Score 206.25 (for 393 correct submissions)
The solution to this problem is pretty straightforward. Iterate through all possible strings of even length, check if they are square, and add all square strings to a set. Having checked all the strings, return the size of the set you have. C++ code follows:
int count(string s)
{
set ans;
for (int len = 1; len <= s.length()/2; len++)
for (int i = 0; i + 2*len <= s.length(); i++) {
if (s.substr(i, len) == s.substr(i + len, len))
ans.insert(s.substr(i, len));
}
return ans.size();
}
PickupBed


Used as: Division One - Level Two:
Since the total number of pipes is very small (at most eight), we can check all the possible orderings of the pipes in the truck. We are to find the minimal length of the truck for every ordering, and return the minimal value of this length among all orderings. To find this, we will fix the position of the first pipe, and place the next pipes one by one as close to the left as possible (but to the right of all already placed pipes).
Value 500 Submission Rate 129 / 465 (27.74%) Success Rate 85 / 129 (65.89%) High Score smell for 437.71 points (11 mins 2 secs) Average Score 257.09 (for 85 correct submissions)
Let (h1, ...,hn) be the heights of the pipes in the ordering. To specify the positions of the pipes in the truck, we will store the position of the pipe as the position of its center.
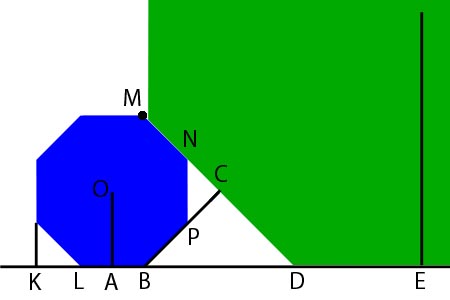
As you can see from the picture, if the height of a pipe is H (blue octagon), the length of OA is H/2. If the length of the side of the octagon is S, then the length of KL is S/sqrt(2). The height of the octagon is equal to 2*KL + LB = (2*S/(sqrt(2))) + S = S*(sqrt(2) + 1), therefore S = H/(1 + sqrt(2)). The length of AB is the half of the side, therefore equal AB = H/(2*(1 + sqrt(2)). The distance between the centers of the octagons is AE = AB + BD + DE. The lengths of AB and DE are known (AB = H/(2*(1 + sqrt(2)), DE = L/(2*(1 + sqrt(2)), where H and L are heights of the octagons), and to find the length of BD we can use the following transformations:
|BD| = sqrt(2) * |BC| = sqrt(2) * (|BP| + |PC|) = sqrt(2) * (|LB| + |PN| / sqrt(2)) = sqrt(2) * (S + S/sqrt(2)) = S*sqrt(2) + S = H.So, the length of BD is equal to the sum of lengths of BP and PC. BP is just the side of the octagon -- equal to S = H/(1 + sqrt(2)). The triangle PCN is an isosceles right-angled triangle (angle PCN is equal to 90 degrees), therefore the length of PC is equal to |PC| = |PN| / sqrt(2), and PN itself is the side of the octagon. Transforming the expression a bit more, we see that the length of BD is equal to the height of the smaller octagon. This also can be proved, looking at triangles BCD and BCM (where M is the vertex of the octagon, which is H units above B). These triangles are both isosceles, both right-angled, and they share a common leg -- therefore they are equal, and the lengths of their hypotenuses are equal too. Therefore, the total distance between the centers of the pipes can be computed as
D = (H + H/(2*sqrt(2)) + L/(2*sqrt(2))),where H and L are heights of the octagons, and H < L.
The pipes can not always be positioned as they are drawn on the picture. This placement is valid only if the point N can be placed "under" the skew edge of the bigger octagon. This is possible, if the height of the point N is less than the height of the skew edge, or, in other words, if ((S + S/sqrt(2)) < L / sqrt(2)). Otherwise, the pipes cannot be placed that close, and the distance between their centers is just the sum of semi-heights of the pipes (H+L)/2.
Knowing the minimal distance between two pipes, we can start calculating the positions for the centers of all pipes one by one. Set the position for the first pipe to 0. For each next pipe i, iterate through previous (i - 1) pipes and compute the leftmost position of the center of the i-th pipe which doesn't collide with any of the first pipes. When you have gone through all the pipes, the only thing left is to compute the length of the truck needed. To do this, iterate through all pipes once again and compute the leftmost and the rightmost points of all pipes. The distance between these points will be the necessary length. The following method computes the minimal length of the truck needed to place all pipes from data without changing their order:
double compute(int[] data) {
double[] center = new double[N];
for (int i = 1; i < N; i++) {
// the side of the i-th octagon
double s = data[i] / (1. + sq2);
for (int j = 0; j < i; j++) {
// the side of the j-th octagon
double a = data[j] / (1. + sq2);
// distance when octagons are placed side-to-side
double dist = (data[i] + data[j]) / 2.;
// its possible to place the i-th octagon "under" the j-th one
if (s + s/sq2 < a)
dist = Math.min(a/2. + s/2. + data[i], dist);
// its possible to place the j-th octagon "under" the i-th one
if (a + a/sq2 < s)
dist = Math.min(a/2. + s/2. + data[j], dist);
// update the minimal position of the center of the i-th octagon
center[i] = Math.max(center[i], center[j] + dist);
}
}
double left = 0;
for (int i = 0; i < N; i++)
left = Math.min(left, center[i] - data[i]/2.);
double right = 0;
for (int i = 0; i < N; i++)
right = Math.max(right, center[i] + data[i]/2.);
return right - left;
}
VectorCostSequence


Used as: Division One - Level Three:
Value 1000 Submission Rate 48 / 465 (10.32%) Success Rate 13 / 48 (27.08%) High Score Petr for 627.43 points (25 mins 18 secs) Average Score 523.61 (for 13 correct submissions)
Let's call an addition that causes the capacity of the vector to increase a jump. The size of the jump will be the capacity of the vector before the jump. If the optimal solution contains several jumps, we can always reorder the sequence of moves to sort jumps in our solution. In other words, if the optimal solution contains several jumps of different size, we can always reorder the moves in the solution to make the jumps of smaller sizes before the bigger ones (keeping the same total number of moves and the total cost of the solution).
The optimal solution, then, can always have the following structure:
... Several additions - each of cost 1 jump of cost 2K - the capacity is doubled to 2K + 1. [optional] - the following part can be not present or can be repeated more than once. removal - the capacity is reduced to 2K. jump of cost 2K - the capacity is doubled to 2K + 1. [/optional] - end of the optional part. Several additions - each of cost 1. jump of cost 2K + 1 - the capacity is doubled to 2K + 2. [optional] - the following part can be not present or can be repeated more than once. removal - the capacity is reduced to 2K + 1. jump of cost 2K + 1 - the capacity is doubled to 2K + 2. [/optional] - end of the optional part. and so on...As you can see, if we ever made the vector to be of the size of N, we must perform N additions and all jumps of sizes 2^k < N, giving us some cost C. If C is greater than d, then N is too big and we can not produce the cost needed. Otherwise, we need to produce the additional cost of (d - C) using optional operations in our algorithm. Since repeating an optional pair of operations results in the cost of (2i + 2) in 2 steps, finding the optimal cost for d (with the maximal size of the vector equal to N) requires finding the optimal split of number (d - C) into the sum of numbers of the form (2i + 2), with each 2i < N.
This problem can be solved using a greedy algorithm -- taking the biggest number of the form (2i + 2) that is less than the necessary cost. The fact that greedy produces the optimal answer can be proved by contradiction, since not taking the biggest number results in more required operations.
To find the optimal solution to the problem, we are trying all possible values for N, computing the answer for each such value and returning the best of them. Since, for each N, we need at least perform N additions, the answer can not be less than N. Therefore, we check only those values of N that are smaller than the best answer we've found so far. Java implementation of this algorithm follows:
public int getSmallest(int d) {
int best = d;
for (int i = 2; i < best; i++) {
int sum = d - i;
int t = 1;
while (t < i) {
sum -= t;
t *= 2;
}
if (sum < 0) break;
best = Math.min(best, i + f(sum, t / 2));
}
return best;
}
int f(int left, int a) {
int cnt = 0;
while (a > 0) {
int p = left / (a + 2);
left -= p * (a + 2);
cnt += p * 2;
a /= 2;
}
return cnt + left;
}
