
|
Match Editorial |
Online Round 4
Wednesday, March 17, 2004
Summary
The last online round of a tournament is usually the hardest of them all. Considering the difficulty of online round 3, would this then be a killer round? Luckily this turned out not to be the case; it required two problems solved at a decent speed to advance to the onsite competition.
The first two problems caused little trouble for most competitors, and almost all submitted both these problems. The hard problem proved to be nasty; after system test only tomek's and grotmol's solutions were still standing, which gave them a 1st and 2nd place. Several of the failed solutions had only minor errors and several more coders were very close on submitting successful solutions on the hard problem.
Most of the favorites had little trouble advancing to the onsite semifinals in Boston, with the notable exception of last years winner dgarthur. The 24 advancers will be representing 12 different countries, showing that TopCoder has successfully extended itself to Europe and other parts of the world.
The Problems
BadNeighbors
Used as: Level One:
Value 250 Submission Rate 44 / 45 (97.78%) Success Rate 41 / 44 (93.18%) High Score dgarthur for 246.77 points (3 mins 15 secs) Average Score 218.55 (for 41 correct submissions)
Given a circular sequence of integers, select a subset of these so the sum is maximized and that no elements in the subset are next to each other in the circular sequence.
The first thing to do is to decide how to handle with the circular data structure. The easiest way to do this is to split it into two linear sequences: one sequence containing all elements except the first, and the other containing all elements except the last. This works since we can't include both the first and the last element in the subset. We can then solve the easier problem concerning a linear sequence of integers twice.
The linear sequence problem can be solved using recursion: let f(x) be the maximum sum after having considered elements 0 to x. Then f(x) = max(f(x-2)+element[x], f(x-3)+element[x-1]). The first sum correspond to including element x in the set, the second sum corresponds to including element x-1 in the set.
It turns out that this recurrence is fast - there is no need to use memoization or dynamic programming. The complexity for this is approximately O(1.32n), which can be deduced by solving the recurrence formula f(n) = f(n-2) + f(n-3).
Most contestants decided to use dynamic programming though, see for instance tomek's solution for such an implementation. It uses basically the same recurrence as above.
BombMan
Used as: Level Two:
Value 500 Submission Rate 41 / 45 (91.11%) Success Rate 31 / 41 (75.61%) High Score antimatter for 462.05 points (8 mins 16 secs) Average Score 341.22 (for 31 correct submissions)
If it weren't for the bombs, this would obviously be your typical shortest path problem, which is solvable with a breadth first search for instance.
Since we do have bombs, it's not as straightforward. First thing to note is that if we blow up a hole somewhere, there's never any point in not going into that square immediately after. There's no gain ever in placing a bomb, move, place a bomb, move etc.
It's also important to realize that we don't have to keep track of which squares are blown up. If we blow up a square and move into it immediately after, there's of course no point in going back to that square later again.
So, we can consider placing a bomb as a way to move into an adjacent square with a cost of 3 time units (place bomb, wait, move) rather than 1 time unit (move). Since the actual changes to the original map (i.e. which squares have been blown up) is not essential knowledge, but only the location of Bomb Man as well as the number of bombs left, we get a small enough search space for a complete search: The size of the search space will be, in theory, approximately at most 50x50x100 = 250,000 states. By checking that we don't enter the same coordinates with fewer bombs and at a slower time, the search space is cut a lot.
Once we have the search space mapped out, we can implement the search algorithm. The most natural choice is to use Dijkstra, by using priority_queue<> in C++ for instance. See speed demon antimatter's solution for a relative clean implementation of this.
It turns out that you can also solve this problem by doing a depth first search by keeping track of the minimum time reached at each state, in conjunction with the pruning condition to abort the search if the Manhattan distance to the exit plus the current time unit is greater than the best distance found so far. I haven't found a test case that causes such a solution to run over time. However, almost all successful solutions used to Dijkstra approach (or a similar version of it).
ScriptLanguage
Used as: Level Three:
Value 1000 Submission Rate 11 / 45 (24.44%) Success Rate 2 / 11 (18.18%) High Score tomek for 552.62 points (31 mins 34 secs) Average Score 505.07 (for 2 correct submissions)
What might look like a daunting task at first can often become more reasonable if divided into several smaller steps. I will describe in detail how this problem can be broken down into three such steps, each of which individually is a fairly easy task.
Step 1: Parsing
The first step concerns the parsing. Always when the input is a bit complicated, I recommend that you convert it to a more suitable data structure. In this problem, such a data structure would be a class describing a line in the code. It should contain the following fields at a minimum:
int instructionType; // 0=IF, 1=ELSE, 2=END IF, 3=RETURN, 4=assignment int variablesUsed; // bitmask int variablesAssigned; // bitmask
I will use bitmasks for representing a set of variables. In this problem this is perfect, since we have 26 variables and there are 32 bits in an integer. Bit 0-25 will thus correspond to variables A to Z, inclusive. Note the use of a bitmask rather than a scalar in variablesAssigned; as you will see it's more convenient to store this information as a bitmask as well. Of course, an empty set is naturally represented by the integer 0.
To parse the input, simply loop over each line and split the tokens using StringTokenizer or similar. Determining the instruction types, variables used and variables assigned are all easy tasks. Note that the function head can be seen as an assignment of multiple variables. That is, instruction type is 4 and variablesAssigned may have several bits set. It should also be obvious that the operands, operators and integer values don't affect anything. So the information stored in the fields above will contains the same knowledge (for our purpose) as the input.
Before proceeding to the next step, I recommended that you verify that the first step has been done correctly. This is easily done by just printing out the variables above for each line and checking with a few examples to see if the values are as expected. This takes around 30-60 seconds and is usually worth the time since you can then forget about the first part and concentrate on the remaining parts.
Step 2: Code flow
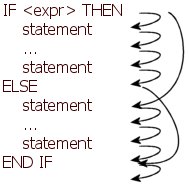
The second step is to figure out the possible code flows. Before doing that, some meaning should be given to the semantics of some statements, specifically the ELSE and END IF statements. As it turns out, implementation becomes easier if we consider the ELSE statement as the last statement executed in the "true-block" of an IF statement, while the END IF statement should always be "executed", see figure.
Now, any given line has either 0, 1 or 2 possible "next lines"; that is, lines that will be executed immediately after the current line. RETURN statements, for instance, have 0 possible next lines, while IF statements always have two. All other instruction have exactly one line. We then want to add to our small class above an array of integers, telling us the possible next lines. For most lines this is easy, it's just the line immediately after it (and in case of RETURN, there's no next line). Exceptions are the IF statements and the ELSE statements:
- One next line for an IF statement is the line immediately following it. The other next line is the line after a matching ELSE statement (if it exist) or the matching END IF statement
- For an ELSE statement, the next line is it's matching END IF statement.
To find the matching ELSE or END IF statement, we can do a look-ahead and keep track of the depth of the IF-ELSE-END IF statements; see the reference implementation in the practice room.
After this step, it's a good idea to again write out the internal information about each line, just to make sure we got step 2 correct.
Step 3: Simulation
One could say that the first two steps were merely the precalculation, while the third step is the actual algorithm. Most likely though, coding the first two steps will take up most of the time spent on this problem if done as mentioned above - this last step is fairly simple to implement if we have the data stored properly.
To determine the warning messages, it should be obvious that if we could simulate all possible code flows, we can determine which code lines never get executed and which variables might be uninitialized. There are actually two ways to do this simulation: simple brute forcing all possible evaluations of the IF statements, or by simulation all flows concurrently:
Brute force
This seems to be the easier solution, but one has to be a bit careful: There can be at most 24 IF statements (50 lines, two are reserved for function head and RETURN, the remaining 48 lines can be divided into 24 IF and END IF statements, respectively), so there are 224 = 16,777,216 possible code flows. This might be doable in C++ if the code is optimized, but I'm not sure I would have trusted that in an actual contest.
However, when one considers this worst case scenario, notice that an IF statement immediately followed by an END IF doesn't really do anything. In fact, the two "next lines" for that IF statement will be the same, so we don't even have to consider evaluating such an IF statement to both true and false. The other worst case with 24 IF statements is when they are all nested like this:
IF expr THEN
IF expr THEN
IF expr THEN
...
END IF
END IF
END IF
In which case there's no problem either, because when we evaluate an IF statement to false, there will be no more IF statements to consider and hence we have only 25 different code flows. So if the IF statements are actually to contain something, there has to be at least one line between IF and END IF, which reduces the number of IF statements to 16, and 216 = 65,536 is a much more reasonable number.
The actual simulation can then be done by recursion. A bitmask is used to keep track of which variables have a value assigned to them, and by using the bitmask operations AND, OR and NOT we can detect when variables are used but not assigned, and update which variables have been assigned. All lines that get executed by some path gets marked as executed. Putting together all the warnings and sorting them appropriately is then a trivial task.
Concurrent simulation
We can actually solve the problem by just looping through all lines one time. The idea is, for each line, to keep a bitmask of which variables are guaranteed to have a value assigned to them. For every line, we check which lines might have been executed right before the current line, i.e. the opposite to "next lines". There can be at most two such "previous lines". The information from these previous lines are then merged, using bitwise AND: a variable is only guaranteed to have a value assigned to it if it's guaranteed to have a value assigned to it in all it's "previous lines". If, at a line, we use a variable that's not guaranteed to have a value assigned to it, we give a warning message.
Additionally, we need to keep track of which lines might be executed (and thus which lines which will never be executed). For each line, if any of it's "previous lines" are executed, then the current line will also be executed. Figuring out the "previous lines" is an easy task when we have the "next lines".
Since we loop through the lines only one time, in order, we can actually generate the warning messages in the proper order right away and thus don't have to do any sorting.
The reference implementation (writer) in the practice room uses the concurrent simulation algorithm, and is also divided into these three steps.
A good exercise is to write a solution that only loops through the lines one single time; i.e. it does all steps at once. Such a solution can't use the simple "look-ahead" approach in step 2 (since that's an extra loop) but must instead use a stack.
