
|
Match Editorial |
Round 1 - W and MW Regional
Thursday, February 20, 2003
Summary
The first round for the students in the W/MW regions was maybe a little easier than for those competing two days ago. The medium and the hard problem had low acceptance rate; the medium had several potential traps and special cases that you could fall in, and the hard involved geometry, a topic that can scare any TopCoder. Luckily the easy problem was easier, and since all that mattered was getting a positive score to advance to the next round (due to the low number of competitors), you only had to solve this one to be safe. bigg_nate got the top score, an impressive 1415.93 points, more than 200 points ahead of the runner-up.
The Problems
FleasFleas
Used as: Level 1:
Value 250 Submission Rate 136 / 154 (88.31%) Success Rate 116 / 136 (85.29%) High Score malpt for 246.22 points
Reference implementation: malpt (room 11)
Implementation
This problem, which is recursive in description, can easily be solved with a recursive approach. Let f(n,k) be the total number of fleas. Of the n fleas, k are infested with n more fleas of which k-5 are infested etc. So the general case is f(n,k)=n+k*f(n,k-5). The terminal case if when k<=0 in which f(n,k)=n (none of the n fleas are infested, so we have n fleas).
It remains to deal with the overflow. If the function ever wants to return a number greater than 10 million or -1, we return -1. We must make sure not to calculate n+k*f(n,k-5) right away - first we must check if f(n,k-5) is -1, then we can calculate n+k*f(n,k-5).
LongestRun
Used as: Level 2:
Value 500 Submission Rate 83 / 154 (53.90%) Success Rate 31 / 83 (37.35%) High Score bigg_nate for 405.00 points
Reference implementation: Yarin (practice room)
Implementation
This problem can be divided into two steps: either the longest run is in one string only, or it is in a concatenation of strings. The first case is trivial, we simply loop through all strings, and for each string we loop through all characters. If a character is the same as the previous character, we increase a counter with 1; otherwise we reset it to 1. The best result found over all strings is stored in some variable.
If the longest run is in the concatenation of several strings, it will be in the following format:
start-string intermediate-string intermediate-string ... stop-string
Clearly the intermediate strings can only be strings containing only one character, namely the last character of start-string and the first character of stop-string (these two characters must of course also be the same). We can now brute-force search for the start-string and stop-string with the following algorithm (pseudo-code):
loop through all possible start-strings
loop through all possible stop-strings
if start-string and stop-string are different
if last char in start-string is the same as first char in stop-string
let c=last char in start-string
let count=number of c characters at the end of start-string +
number of c characters at the beginning of stop-string
loop through all remaining strings
if string only contains letter c
count=count+string length
end if
end loop
if count is greater than best found so far
update best
end if
end if
end if
end loop
end loop
Tether

Used as: Level 3:
Value 1000 Submission Rate 28 / 154 (18.18%) Success Rate 8 / 28 (28.57%) High Score bigg_nate for 780.13 points
Reference implementation: dmwright (room 9)
Implementation
This problem reduces to the following geometry problem: given a circle and two points, of which one point lies on the circle, calculate the shortest distance between them under the constraints that you may not "walk" (or whatever) inside the circle.
One of the points was (0,-r), where r is the radius of the circle, while the other point is x,y. Again there are two cases to consider: either the circle interferes with the shortest path, or it doesn't. In the latter case (which happens when y <= -r) it's simply the Euclidean distance between the two points, calculated using Pythagoras formula.
In the trickier case, we start at 0,-r (point A) and walk along the circle perimeter, and then at some point (call it P) continue straight ahead to x,y (point B) - see figure. Clearly we should try to walk as little as possible along the circle and as soon as possible in a straight line.
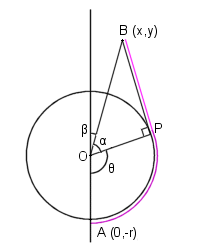
Using the notation in the picture, we see that the OPB is a right triangle - this will always be the case for the shortest path! We can now set up the following equations:
|OB| = sqrt(x*x + y*y) |OP| = r |BP| = sqrt(|OB|*|OB| - |OP|*|OP|) cos(a) = |OP|/|OB| tan(b) = x/y t = p - a - b; |AP| = t*r |AB| = |AP| + |BP|
It's slightly trickier than this because you have to consider in which quadrant B is. This can be solved using atan2 instead of atan, and taking the absolute value of x (which won't affect the answer because of symmetry). For implementation details, see the reference solution.
