
|
Match Editorial |
Regional SemiFinals
Wednesday, March 5, 2003
Summary
The regional semifinals caused some huge upsets when top seeded John Dethridge was knocked out, together with other high ranked coders such as reid and malpt (reid did not show up at all). The cutoffs for the different regions differed quite a lot; John Dethridge would for instance have qualified had he competed in any other region. Top scorers were bigg_nate and Yarin. The problem set was arguably one of the better in this CC, with a mix of math, dynamic programming and geometry.
The Problems
Ordered
Used as: Level 1:
Value 200 Submission Rate 127 / 129 (98.45%) Success Rate 111 / 127 (87.40%) High Score bigg_nate for 193.50 points
Reference implementation: Yarin (room 2)
Implementation
I suspect an easy (200 pts) first problem was selected just to make sure all regional finals would have 10 competitors... Still, the problem had some pitfalls, the major one being spelling errors, even though the notes warned about that.
Given a sequence of numbers, we should deduce if it's strictly increasing, strictly decreasing, non-decreasing or non-increasing (which I believe are the proper terms). To check the first two cases, just make sure every value is greater (smaller) than the previous value. If this is not the case, set a flag. We do the same for the other two cases, but instead check that every value is greater-or-equal (smaller-or-equal) to the previous value.
Depending on the results, we should either append the mean of the values (reduced fraction, so we need to use GCD) to the result string or the frequency of the most common element. It could also be that none of the four types of sequences applied, in which case we simply returned "NOTHING".
GreedyChange
Used as: Level 2:
Value 500 Submission Rate 73 / 129 (56.59%) Success Rate 46 / 73 (63.01%) High Score bigg_nate for 444.78 points
Reference implementation: bigg_nate (room 13)
Implementation
This is a typical DP (dynamic programming) problem. It consists of two parts - first we calculate the optimal way of handing back coins for all values up to a limit. Then for each such value we compare with the greedy method. If the greedy method is worse than the optimal, we return this value. Otherwise we keep going until we hit the limit (see below), and once we hit it, we return -1.
To calculate the optimal way of handing back coins, we use induction. Assume we know the fewest coins possible for all integers x<k (this value is stored in a big array, opt[], where opt[x] = the fewest coins possible when the value is x). Now we should calculate the fewest coins possible when the value is k. The idea is that for any value k>0, we must first give back one coin. After that, the remaining value is less than k, and for that value we already know the fewest coins possible (by induction). So, we loop through all denominations (call them d[i]), check opt[k-d[i]], and pick the minimum of these values. Thus,
opt[k]: for all denominations d[i]: min(opt[k-d[i]])+1
For the greedy approach, we can use induction again. Assume we know that the greedy method equals the optimal method for all integers x<k. That is, opt[x]==greedy[x]. Now, in order for greedy to work on the value k, opt[k-d_max]+1 must equal opt[k], where d_max is the highest denomination less than or equal to k. The reason for this is that this is the coin we will hand back first; after that we know by induction that greedy works for the value k-d_max, so the number of coins that we hand back by this method is opt[k-d_max]+1.
In order for the program to run in time, we need a quick way to find out the largest coin less than or equal to the current value. This can be solved nicely by first sorting the coins, and then as we loop through the values, we keep updating which coin is currently the largest less than or equal to the value - the reference implementation handles this nicely.
This is all fairly standard stuff. What maybe made this problem slightly harder is to figure out how long you should search before deducting that greedy works on all values. I believe most people simply guessed (I know I did), with the hint from the last example case, that if greedy worked for all values up to 2N (where N was the largest denomination), it worked for all values. Below follows a proof that this is actually the case:
Assume greedy works for all numbers less than k, k>2N, where N is the largest coin. We will now prove that greedy works for k as well. By assumption, we have the true recurrence that opt[k]=min(opt[k-j]+1) where j is the value of some coin. Now, we know that the greedy solution works for opt[k-j] and also that k-j>N. Thus, opt[k-j]=opt[k-j-N]+1. So, we can rewrite this as:
opt[k]=min(opt[k-N-j]+1)+1
since the greedy solution for k-j involves using a coin valued at N (k-j>N). Now, we can rewrite min(opt[k-N-j]+1) as opt[k-N], from our original recurrence, and thus we get:
opt[k]=opt[k-N]+1
which is what the greedy solution gives. QED (proof by lbackstrom)
SolidArea
Used as: Level 3:
Value 1000 Submission Rate 49 / 129 (37.98%) Success Rate 39 / 49 (79.59%) High Score Yarin for 824.44 points
Reference implementation: Yarin (room 2)
Implementation
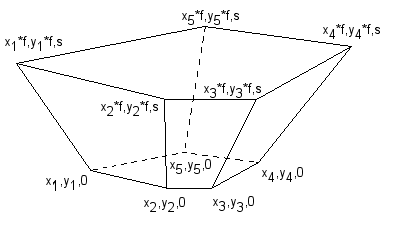 Given a polygon on the xy-plane, the polygon is moved "up" along
the z-axis while being enlarged. This creates a solid, see picture below. The problem is to calculate
the area of all the surfaces of this solid.
Given a polygon on the xy-plane, the polygon is moved "up" along
the z-axis while being enlarged. This creates a solid, see picture below. The problem is to calculate
the area of all the surfaces of this solid.
The solid has two kinds of surfaces: the two polygonal surfaces (top & bottom), and the n faces. The problem constraint guarantees that the solid will be "nice", no crossing surfaces or any such (in fact, I don't think such a figure would be called a solid!).
The area of the two polygonal surfaces can be calculated with a formula that, if you don't know it, you should learn!
PAREA = ((x1*y2-x2*y1) + (x2*y3-x3*y2) + .... + (xn*y1-x1*yn)) /2
where the polygon points are (x1,y1), (x2,y2), ... , (xn,yn). Depending on whether or not the polygon points are clockwise or counter clockwise, you may have to negate the value above.
It remains to calculate the area of the n sides. Each side is a trapezoid with coordinates in 3D. The coordinates for the trapezoid are (xi,yi,0),(xi+1,yi+1,0),(xi*f,yi*f,s),(xi+1*f,yi+1*f,s) where xi,yi are the original coordinates for the polygon, f is the enlargement factor and s is the shift value (how much the polygon is moved up along the z-axis).
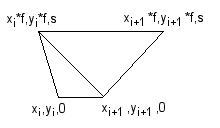 Now, calculating the area of a trapezoid is fairly simple - multiply the average base length with the height. The problem here is that the trapezoid is in 3D
and calculating the height requires some elementary knowledge in linear algebra. Instead I went
for a different approach: I divided the trapezoid into two triangles and calculated the area
of those using Herons formula:
Now, calculating the area of a trapezoid is fairly simple - multiply the average base length with the height. The problem here is that the trapezoid is in 3D
and calculating the height requires some elementary knowledge in linear algebra. Instead I went
for a different approach: I divided the trapezoid into two triangles and calculated the area
of those using Herons formula:
TAREA = sqrt(p*(p-a)*(p-b)*(p-c))
where a, b, c are the sides of the triangle (calculated from the coordinates using Pythagoras formula) and p is half the perimeter, (a+b+c)/2.
That's basically it. The answer is sum of all these areas, rounded down. Check the reference implementation for details.
