
|
Match Editorial |
Saturday, October 18, 2008
Match summary
American (1-st, 4-th and 6-th places) and Chinese (2-nd and 3-rd places) coders occupied most of the top spots for this SRM. neal_wu won the match having 5 successful challenges, crazyb0y was second, and ACRush was the third with the most impressive challenge phase of the day (+375 points). Rating favorite Petr was only 9-th, significantly lowering his rating. In Division 2, john_rapera and [Hanney] got the 1-st and 3-rd places thanks to high scores on all problems, while tgoulart was second thanks to a +150 challenge phase.
The Problems
MultiNumber

Used as: Division Two - Level One:
Value 250 Submission Rate 896 / 952 (94.12%) Success Rate 536 / 896 (59.82%) High Score oa12gb for 247.58 points (2 mins 49 secs) Average Score 203.43 (for 536 correct submissions)
As it often happens, to solution to the easy problem in Division 2 was pure brute force. You try all ways to split the number into 2 parts, multiply all digits in each of the parts, and check whether the results are the same. The only trick in this problem is to make sure that you don't leave any of the parts empty. See Archimedean1's solution for an implementation.
PrimeSoccer

Used as: Division Two - Level Two:
Used as: Division One - Level One:
Value 500 Submission Rate 318 / 952 (33.40%) Success Rate 288 / 318 (90.57%) High Score Archimedean1 for 469.43 points (7 mins 20 secs) Average Score 293.31 (for 288 correct submissions)
Value 250 Submission Rate 609 / 676 (90.09%) Success Rate 606 / 609 (99.51%) High Score ainu7 for 246.69 points (3 mins 18 secs) Average Score 193.17 (for 606 correct submissions)
This problem required basic knowledge of probability theory and combinatorics.
First, let assume we know the probability that team A will score a prime number of goals (lets call this probability Pa) and that team B will score a prime number of goals (Pb). Since those events are independent, the probability that at least one team scores a prime number of goals will be equal to Pa + Pb - Pa * Pb.
Now lets try to compute the probability that a team will score a prime number of goals. A 90-minute game contains only 18 5-minute intervals, and a team can score at most one goal during such interval, therefore a team can score at most 18 goals. Now we need to find all prime numbers Pi not greater than 18, compute the probabilities for each team to score exactly Pi goals, and sum those probabilities to get numbers Pa and Pb. To find primes you may either use the sieve of Eratosthenes, or just pre-code them into an array.
The last but not the least - how to compute the probability for a team with skill S to score exactly K goals during a game? Assume that we've selected K intervals and want to compute the probability that the team has scored in each of those K intervals and did not score during any other interval. This probability is equal to SK * (1 - S)(18 - K) (SK is the probability to score during K intervals, and (1 - S)(18 - K) is the probability not to score in any of other (18 - K) intervals). And the last step - since there are 18! / (K! * (18 - K)!) ways to select K intervals, the final answer is Pa = (Sum over all primes K) (18! * SkillOfTeamAK * (1 - SkillOfTeamA)(18 - K) / (K! * (18 - K)!). Of course, to compute Pb you'll need to replace SkillOfTeamA by SkillOfTeamB.
BirthdayCake

Used as: Division Two - Level Three:
Value 1000 Submission Rate 145 / 952 (15.23%) Success Rate 21 / 145 (14.48%) High Score unbing for 838.05 points (13 mins 1 secs) Average Score 575.97 (for 21 correct submissions)
Brute force problems are my favorites - check all possibilities (different cakes with exactly K ingredients), find the one which will be eated by the largest number of friends and return. Oops, unfortunately we can have too many fruits, so we won't be able to check all possible cakes with 25 out of possible 50 ingredients within a reasonable time limit. On the other hand, I still have a feeling this problem can be brute-forced, and I try to use a brute-force solution when possible - since it is the easiest to implement and to verify.
If we can't check all possible cakes, maybe we can brute-force over the answer? There can be at most 20 friends, which screams 2^N algorithm. What if we'll try all possible groups (subsets) of friends, computing the number of 'bad' fruits (a fruit is bad if at least one person of the subset will not eat it). Then we discard subsets which result in less than K good fruits and return the maximal number of friends in other subsets.
The idea sounds good, but we need to make sure the solution will run in time. You can easily optimize computing the number of friends in a group, store the fruits someone doesn't like as a bitmask, memoize the fruits which are not liked by a group, don't check the groups which contain less people than the best answer we've already found, etc. You can even try binary searching over the answer, when on each step of binary search you check only groups of the same number of people. See leshiy239's solution for an implementation.
CavePassage

Used as: Division One - Level Two:
Value 500 Submission Rate 324 / 676 (47.93%) Success Rate 81 / 324 (25.00%) High Score bmerry for 403.67 points (14 mins 37 secs) Average Score 264.75 (for 81 correct submissions)
This problem is a mix of a classical algorithm (BFS) and a complicated implementation. In therms of graph theory, the problem asks us to find the shortest path in a weighted graph, where each vertex is described by two parameters: the set of people who are on the entrance of the cave and by the position of the map (whether a person with a map is on the entrance or on the exit of the cave). In the initial position everybody is in the entrance and map is on the entrance as well, and at the end all people are at the exit with the map. Edges between vertices correspond to groups which pass through the cave, and you must be very careful to add only those groups which are allowed to do so.
To make your sol run in time, you may want precompute some oftenly used values - like the time needed by a group to pass the cave (time needed for group of people A, B, ... Z to pass the cave is equal to the maximum of two numbers - the time needed for group B, ... Z, which can be memoized, and the time for person A) or check whether the group can pass through. On the other hand, be careful not to "overoptimize" your solution. One of the most common mistakes was assuming the optimal solution will never require more than one person to carry the map back to the entrance. See bmerry's solution for an implementation.
WorkersOnPlane

Used as: Division One - Level Three:
Value 1000 Submission Rate 89 / 676 (13.17%) Success Rate 31 / 89 (34.83%) High Score crazyb0y for 856.98 points (12 mins 1 secs) Average Score 577.63 (for 31 correct submissions)
This problem can be split into several logical parts. First, you need to parse the input, and enumerate all workers, silver and gold mines. Second, you need to check which mines can be assigned to each worker (this can be done, for example, by running a simple BFS starting at each of the workplaces).
And the last but not the simplest - you need to assign mines to the workers in an optimal way. If you were to assign workers to only one type of mines (for example, silver ones), you would have used bipartite matching algorithm, which was used multiple times in previous TopCoder problems. Since this problem asks you to assign workers to two differents types of resources, so you'll need to use a general version of bipartite matching - maximal flow algorithm.
First intention is to build a graph to represent our problem. This part is simple - each mine and each workplace will represent a vertex, and a worker vertex will be connected to a mine vertex only if the corresponding mine is reachable by worker. Since we want each unit of the flow to come through worker vertex and two mine vertices of different types, we may want to force it by connecting the source of the flow to all gold mines, and connecting all silver mines to the sink. To make sure that each mine is used only once, we will set the capacity of all edges to one unit.
It seems the graph we built will solve our problem, but after some testing you may notice it sometimes returns answers greater than the correct one. For example, for K = 5 and the following map:
SS W. GG
our algorithm will return 2. It is easy to find the reason: our graph looks as the following (blue circle represents source, yellow - gold mines, black - worker, grey - silver mines, green - sink).
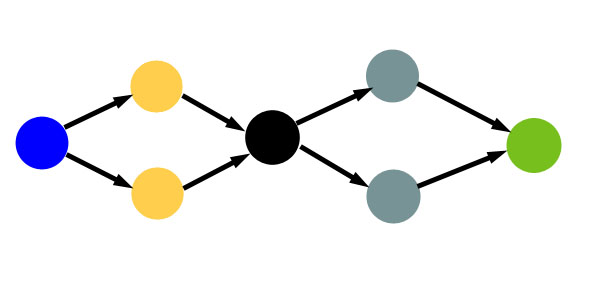
It is clear why we do return 2: because our network allows worker to work on 2 gold and 2 silver mines at ones. We need to change our network a bit to limit workers to at most one gold and one silver mine. This can be done by adding a special vertex for each worker, connecting it to the initial worker vertex by an extra edge of capacity one, and redirecting all worker's flow through that edge:
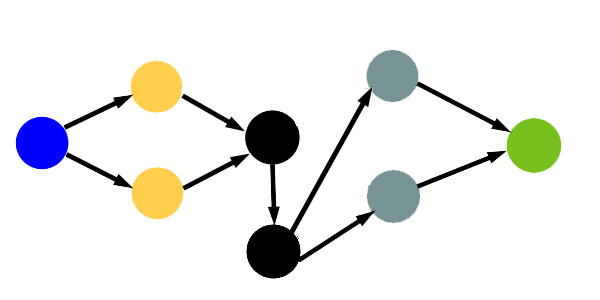
Once you get the idea and build a proper network, the rest of the solution is just implementing a reasonably fast maximal flow algorithm, which shouldn't be a problem if you got so far (if it IS a problem, just implement it 3-5 times and the problem will disappear. The examples of the implementation can be found either in our tutorial, or in Petr's solution).
