
|
Match Editorial |
Wednesday, September 24, 2008
Match summary
This SRMs didn't light any new stars - Division 1 was routinely won by Petr, and no newcomers made it into the top-50 of Division 2. Petr won the round with a little help of 5 successful challenges, JongMan was second, and pparys, the author of the only correct solution for the hard problem, rounded the top-three.
In Division 2, SuperLight was less than 100 points behind pab2 (the winner of the round), but finished only fourth - Biskup and razimantv finished head-to-head on the second and third places respectively.
The Problems
ColumnDiagramPerimeter

Used as: Division Two - Level One:
Value 250 Submission Rate 521 / 548 (95.07%) Success Rate 418 / 521 (80.23%) High Score [MinWoo] for 249.03 points (1 mins 46 secs) Average Score 219.76 (for 418 correct submissions)
To compute the perimeter of the diagram, we'll first compute the total summary length of all horizontal and all vertical segments, and then we'll have the perimeter as the sum of those two values.
Computing the sum of all horizontal segments is easy - each column produces exactly 2 horizontal segments of length 1, so the total "horizontal perimeter" will be equal to 2 * (number of columns). Computing the total length of all vertical segments is a bit harder. First, we must count all differences in lengths between neighboring columns. For example, if a = {2, 5, 3}, then the difference between 2 and 5 will result in a vertical segment of length 3, and the difference between 5 and 3 will produce a vertical segment of length 2. In other words, the length of each vertical segment is the absolute difference in the heights of the corresponding columns.
We are almost done, but we should count also the left side of the very first segment, and the right side of the last segment. See Sane's solution for an example of implementation.
Undo

Used as: Division Two - Level Two:
Used as: Division One - Level One:
Value 500 Submission Rate 346 / 548 (63.14%) Success Rate 148 / 346 (42.77%) High Score garfi for 476.78 points (6 mins 19 secs) Average Score 318.52 (for 148 correct submissions)
Value 250 Submission Rate 414 / 419 (98.81%) Success Rate 329 / 414 (79.47%) High Score JongMan for 246.38 points (3 mins 27 secs) Average Score 197.93 (for 329 correct submissions)
In this problem you need to carefully implement the described algorithm, and make sure you handle the nested undo correctly. As one of the ways to do that, you should go backwards from the last operation to the first, and mark operations as "undone" or "valid". An operation is "undone" if there exists a later valid "undo" operation, or valid otherwise. Having all operations marked, you concatenate the letters from all valid "type" operations and return them as a string:
public class Undo {
public String getText(String[] commands, int[] time) {
int n = commands.length;
boolean[][] can = new boolean[n][n];
for (int i=0; i < n; i++)
if (commands[i].startsWith("undo")) {
int t = Integer.parseInt(commands[i].split(" ")[1]);
for (int j=0; j < i; j++)
if (time[i] - time[j] <= t)
can[j][i] = true;
}
boolean[] exists = new boolean[n];
for (int i = n-1; i >= 0; i--) {
exists[i] = true;
for (int j=i+1; j < n; j++)
if (can[i][j] && exists[j])
exists[i] = false;
}
String res = "";
for (int i=0; i < n; i++)
if (commands[i].startsWith("type") && exists[i])
res += commands[i].split(" ")[1];
return res;
}
}
CactusCount


Used as: Division Two - Level Three:
Value 1000 Submission Rate 34 / 548 (6.20%) Success Rate 5 / 34 (14.71%) High Score pab2 for 565.35 points (30 mins 21 secs) Average Score 501.97 (for 5 correct submissions)
The major part of the problem is to find a way to check whether a connected component is a cactus. According to the definition of cactus, a component will not be a cactus if at least one vertex will be a part of at least two simple cycles. If so, then there exists a vertex V, which is a part of at least two simple cycles V - A - ... B - V and V - C - ... - D - V, and out of vertices (A, B, C, D) there are at least 3 different (so, for example, if A and D are the same vertex, then B and C are different). Since vertices A, B, C and D are parts of a cycle, then a path from vertex A to V will remain even if we'll remove edge VA from the graph.
So, to check whether a connected component is a cactus, we will check all vertices V of the component. For each vertex V, we iterate through all its neighbours Ni and count how many of them will stay connected to V even after edge V-Ni is removed. If some vertex V has at least 3 such neighbours, then the vertex is bad and the component containing V is not a cactus.
The only part left in this problem is to split graph into connected components, which is a text-book problem and can be solved by either DFS or BFS. Having graph split into components, just count the components which do not contain bad vertices.
NimForK

Used as: Division One - Level Two:
Value 500 Submission Rate 187 / 419 (44.63%) Success Rate 44 / 187 (23.53%) High Score JongMan for 448.26 points (9 mins 53 secs) Average Score 242.76 (for 44 correct submissions)
Like many combinatorial games problems, this one is solvable with dynamic programming. The solution can be broken into two steps. First, lets identify for which numbers of stones the player to make the next move has a winning strategy regardless of how the other players move. This is quite similar to identifying winning positions in usual 2 players game, but things become a little bit more complicated because we can have more than 2 players. To solve this part we can calculate the following values:
- canWin(i): assume there are currently i stones left on the table. Does the player to make the next move have a winning strategy regardless of how the other players move?
- canMakeNotWin(i, j): assume there are currently j stones and player i (i ≥ 1) should make the next move. Do players 1, 2, ..., k-1 have a collaborate strategy that makes it certain that player 0 won't win the game regardless of his moves?
To calculate this functions, the following rules can be used:
- canWin(i) is true if we can take all i stones in one move or if we can take some number of stones x < i such that canMakeNotWin(1, i - x) is false (after we take x stones, the player 1 will be left with i - x stones; we can win if from this situation the other players don't have a collaborate strategy that makes it certain that we don't win).
- canMakeNotWin(i, j), i ≠ k - 1, is true if there are no possible moves for i-th player (nobody will win in this case), if he can take all stones in one move or if there is a move consisting of taking x < j stones such that canMakeNotWin(i + 1, j - x) is true (after we take x stones, the player i + 1 will be left with j - x stones and should be able to successfully proceed the collaboration strategy that forces the player 0 to not win).
- canMakeNotWin(k - 1, j) is true is there are no possible moves for i-th player, if he can take all stones in one move or if there is a move consisting of taking x < j stones such that canWin(j - x) is false (the player 0 will be left with j - x stones and should not be able to win).
Now, the second step of our solution consists of calculating the sets winPrb(i), 1 ≤ i ≤ n. Each of these sets contains all players who have a non-zero probability of winning the game, which starts from i stones and player 0 makes the first move. If canWin(i) is true, then player 0 will follow his winning strategy, so winPrb(i) = {0}. If canWin(i) is false, then we need to check whether player 0 can ensure his win with a non-zero probability (assuming all other players follow the same strategy). To do this, let's iterate through all possible moves x and check sets winPrb(i - x). Suppose at least one of this sets contain player k - 1. It means that if player 0 started the game with i - x stones, then player k - 1 would have a positive chance to win. Similarly, if player 1 (the next after 0) started the game with i - x stones, then player 0 (the next after k - 1) would also have a positive chance to win. So moves x such that winPrb(i - x) contains player k - 1 guarantee positive winning chances to player 0. If there's at least one such move, he will randomly do one of such moves.
Let's define the right shift of a set A as the set B where each player i from the set A is replaced by player i+1 (player k-1 is replaced by player 0). If player 0 started the game with i - x stones, then winPrb(i - x) would give us all players who have chances to win. Similarly, if player 1 started the game with i - x stone, then all players who can win would be described by the right shift of winPrb(i - x). Now it's easy to see the algorithm of calculation of winPrb(i): if at least one of sets winPrb(i - x) contains player k - 1, then winPrb(i) is the union of the right shifts of all such sets, otherwise winPrb(i) is the union of all possible sets winPrb(i - x).
After winPrb is calculated, the answer is just winPrb(n).
Exercise. It may seem true that canWin(i) is true if and only if winPrb(i) = {0}. If it were true, there would be no need in calculating canWin and canMakeNotWin, so solution would become much easier. Show that it's not true by constructing an example where winPrb(i) = {0} and canWin(i) is false.
CactusAutomorphisms

Used as: Division One - Level Three:
Value 1000 Submission Rate 4 / 419 (0.95%) Success Rate 1 / 4 (25.00%) High Score pparys for 383.93 points (64 mins 15 secs) Average Score 383.93 (for 1 correct submission)
The writeup for this problem is quite long, so for convenience it's broken into 3 parts.
1. Investigating the structure of a cactus. Before starting to solve the problem, let's answer the question: what does a cactus look like? To do this, let's take some cactus and find all bridges in it (bridge is such an edge that after its removal the graph becomes broken into two connected components). If we temporarily remove all bridges from the graph, it will become broken into several connected components. If some component had 2 or more simple cycles, then, as any 2 cycles doesn't have common vertices, there would be no way to make this component connected. Therefore, each connected component is a single vertex or a single simple cycle.
Now, let's replace each simple cycle by a single vertex and return all removed bridges back. What does the obtained graph look like? Note that any edge that lies in at least one simple cycle can't be a bridge (removal of such edge would still preserve connection between its ends by the other edges of the cycle). It means that all bridges don't lie in cycles and our graph doesn't have cycles. Additionally, it's not hard to see that the graph is still connected, therefore we've obtained a tree.
So, each cactus can be obtained from some tree by choosing some vertices of the tree and replacing each of them by a simple cycle (edges which have the replaced vertex as one of endvertices can be assigned to any vertices of the cycle).
We've discovered that cacti are in fact a generalization of trees. As trees form a simpler class of graphs, let's first solve the automorphism problem for trees and then try to generalize our solution on the case of cacti.
2. Counting the automorphisms of a tree. So, we are given a tree. If we choose an edge of this tree and one of two directions of this edge, the obtained arc will point on some subtree:
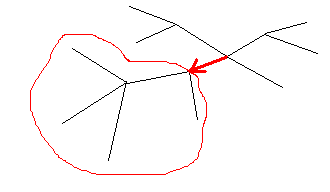
For each such subtree let's count the number of its automorphisms with the following restriction: the root vertex is mapped onto itself. To do this, it's helpful to assign a string code to each subtree in such way that two subtrees are assigned the same code if and only if there exists an isomorphism (i.e. bijection between vertices of the first subtree and vertices of the second subtree such that edge in first subtree exists if and only if there exists an edge between corresponding vertices in second subtree) between them where roots of both subtrees are mapped onto each other. To calculate the code for a subtree, the following recursive procedure can be applied:
- If subtree consists of a single vertex, its code is an empty string.
- Otherwise, consider all sons of the root and their subtrees. Let's code the subtree by some its traversal, where '0' means going deeper from root and '1' means going back to root. The problem with such approach is that two isomorphic subtrees can have their sons' subtrees in different orders and therefore we can obtain different codes during their traversals. To resolve this, we need to fix some order of sons traversal for the root. For example, we can recursively calculate the codes for each son's subtree and then traverse sons in lexicographical order of their subtrees' codes.
To clarify this approach, let's consider a small example of a subtree (root is the topmost vertex):
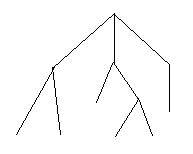
The left root son's subtree has a code of "0101" (go down, go up, go down and then go up), the middle subtree has a code of "01001011" and the right subtree has a code of "01". The lexicographical order of codes is "01", "01001011", "0101", so the whole subtree has a code of "00110010010111001011".
Now, to calculate the required number of automorphisms for a subtree, note that sons of the root vertex must be mapped onto themselves and each two sons mapped onto each other must have isomorphic subtrees (i.e. their codes must be the same). So we can take codes of all sons' subtrees and divide them into groups of the same codes. Within each group we can permute sons arbitrarily. That is, the number of ways to map sons is A = product(factorial(group size)) taken by all groups. The number of ways to map other vertices is B = product(number of automorphisms of subtree) taken by all sons' subtrees. And the total number of automorphisms for a subtree is A * B.
When the number of automorphisms for each subtree is calculated, we're really close to solving the problem completely. If we take arbitrary leaf of our tree and consider the only arc that goes out of him, this arc points on the whole tree (except the leaf itself). So the number X of automorphisms for the subtree pointed by this arc is almost the answer for our problem. I say "almost" because earlier we've calculated only automorphisms where the root is mapped onto itself. In fact, we can try to map the taken leaf onto some other leaf of the tree. Of course, all these leaves should produce isomorphic subtrees, i.e. subtrees with the same codes. So to obtain the final answer we should multiply X by the number of leaves that produce the subtree with the same code as the subtree produced by the taken leaf.
3. Going back to cacti. Ok, we're done with trees and what about cacti? The approach for cacti is similar, but slightly harder. If we take an edge that doesn't lie within a cycle and one of 2 its directions, it will point out on some subcactus. There are two possibilities: the arc points on a single vertex or on a cycle:
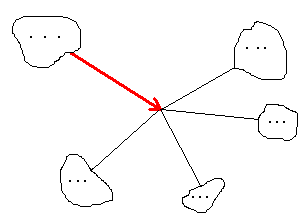 | 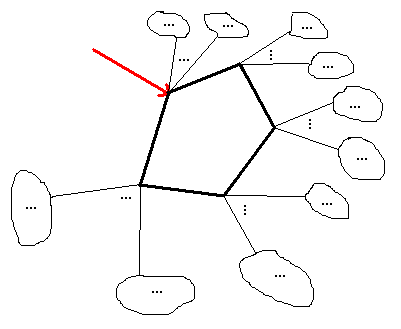 |
As with trees, for each subcactus we need to calculate a code which is the same for isomorphic pairs of subcacti. And, again, it's calculated as a DFS traversal made by some rules:
- if arc points on a vertex, traverse all root sons' subcacti in the lexicographical order of their codes;
- if arc points on a cycle, traverse it clockwise. For each cycle vertex traverse all subcacti that go out from it in the lexicographical order of their codes. Do the same for counter-clockwise traversal of the cycle. Select the lexicographically smallest among the codes for both traversals.
Note that whereas in case of trees we needed just two characters for codes ('0' - go deeper, '1' - go back), in case of cacti we need third character ('2' - go by a cycle edge).
Given the codes for each subcactus, the number of its automorphisms is calculated as follows:
- If arc points on a vertex, group the sons' subcacti with the same codes and return (product(factorial(group size)) by all groups) * (product(number of subcactus automorphisms) by all subcacti).
- Set result to 1. Traverse the cycle clockwise. For each cycle vertex group all subcacti with the same codes and multiply the result by product(factorial(group size)). For each subcactus we've met, multiply the result by the number of its automorphisms. If clockwise and counter-clockwise cycle traversals produce the same codes, multiply the result by 2.
Finally, to calculate the answer, do the following. If each cactus cycle is replaced by a single vertex, we'll obtain a tree. Take any leaf in this tree and a cycle or a vertex from cactus that corresponds to this leaf. Call such cycle/vertex a leaf cycle/vertex. For each leaf cycle/vertex there's only one non-cycle edge that goes out of it. If we take this edge and orient it out of this cycle/vertex, it will point on some subcactus. Let's say that this subcactus is associated with given leaf cycle/vertex. Now fix arbitrary leaf cycle/vertex and calculate the amount of leaf cycles/vertices that have the same size and the same code of associated subcactus as the fixed cycle/vertex. Multiply this amount by the number of automorphisms of subcactus associated with the fixed cycle/vertex. If the fixed cycle/vertex is not a vertex, but a cycle, multiply the result by 2. This is our final answer.

