Match Editorial

Match summary

In the first division competitors faced a technical easy problem, a tricky hard, and a medium where they had to choose between two completely different approaches. janos enjoys his first match victory thanks to his good performance on all three problems. He was followed by microsoft and Zhukov_Dmitry. Victory in the second division went to damnerd.

The Problems

Value	250
Submission Rate	795 / 866 (91.80%)
Success Rate	716 / 795 (90.06%)
High Score	KnightOfTheSun for 249.27 points (1 mins 32 secs)
Average Score	212.96 (for 716 correct submissions)

This problem is about how to implement the Rev(x) function. This can be done in many ways. The "classic" aporoach is illustrated in KnightOfTheSun's solution. Another approach is to convert integers to strings, reverse them, and parse the integers back. See rudolfking's C# solution for the reference.

Value	500
Submission Rate	234 / 866 (27.02%)
Success Rate	141 / 234 (60.26%)
High Score	peterLiang for 420.35 points (12 mins 52 secs)
Average Score	251.79 (for 141 correct submissions)

Value	250
Submission Rate	584 / 640 (91.25%)
Success Rate	470 / 584 (80.48%)
High Score	arti_kz for 243.81 points (4 mins 33 secs)
Average Score	174.44 (for 470 correct submissions)

This problem was a technical one. All you needed to do was described in the problem statement: iterate over all the substrings and select the best one. You also need to resolve ties carefully. See darnley's solution for clear implementation in Java and ACRush's soluton in C++.

Value	1000
Submission Rate	28 / 866 (3.23%)
Success Rate	3 / 28 (10.71%)
High Score	damnerd for 436.60 points (48 mins 10 secs)
Average Score	359.09 (for 3 correct submissions)

The first thing you need to understand clearly before solving this problem is the following fact. Consider two independent random variables X and Y, uniformly distributed over some range [A, B]. Then their sum can possess values in range [2A, 2B], but values from this range will come with different probabilities! To illustrate this fact consider throwing two coins: the probability to get two "heads" or two "tails" is 0.25 each, but you have a 50% chance to get one "head" and one "tail".
Now let's go back to the problem. First of all let's substract the length of our first jump from all opponent's results. This will reduce the problem to a "double jump", where the length of each of the two jumps is a random variable. The core part of the solution is implementing the following function: F(z) = probability that your two remaining jumps will have total length at least z. Those of you who are familiar with theory of probablity might now that such function F(z) is called a distribution function. In our problem z = x + y, where x and y are random values, uniformly distributed in range [lower, upper]. Let's illustrate this on the cartesian plane Oxy.

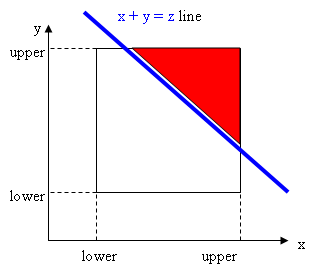F(z) is proportional to the area of the red figure above the line x + y = z. Indeed, each point inside this figure has coordinates that in sum are greater than z. Some basic calculations allows us to find F(z) as:

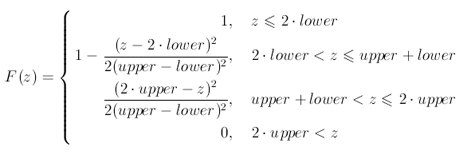Now, lets sort the opponents results in the descending order. In this case our chance to get the first plase will be F(opponents[0]). Chance to get second place F(opponents[1]) - F(opponents[0]), third: F(opponents[2]) - F(opponents[1]) and so on.

Value	500
Submission Rate	240 / 640 (37.50%)
Success Rate	130 / 240 (54.17%)
High Score	jbernadas for 443.34 points (10 mins 25 secs)
Average Score	278.39 (for 130 correct submissions)

There are two different approaches for this problem. The first one is just to google for "cube net" and find out that there are only 11 distinct cube nets. After that you just need to compare the figure from the input with these eleven "canonical" cube nets carefully. This is still not a trivial coding task and many competitors, who selected this approach, failed it. See darnley's solution for the implementation details.
Another approach is to find any position with an '#' and "put" the cube there. After that start "rolling" the cube recursively while you have adjacent '#' cells. One each roll assign the the cell to the surface of the cube that touches it. At the end check if all the '#' cells had an assigned surface. See jbernadas's solution for clear implementation.

Value	1000
Submission Rate	109 / 640 (17.03%)
Success Rate	12 / 109 (11.01%)
High Score	kefir for 799.98 points (15 mins 0 secs)
Average Score	553.99 (for 12 correct submissions)

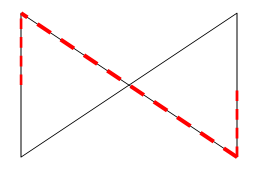
Let's start from an example that illustrates that both two points where the maximal walking distance is achieved are not necessary be the vertices of the graph.

There are several approches for this problem. But in any case we need to calculate shortest distances among each pair of vertices, and to iterate through all pairs of edges. Now, when the two edges (let's call them AB and CD) are fixed lets find points p from AB and q from CD with the maximal possible walking distance between them. Basicly, there are four candidates for the shortest p-q path: p-A-C-q, p-A-D-q, p-B-C-q, p-B-D-q. If we think about p and q as a real-valued parameter in range [0, AB] and [0, CD] correspondingly, the length of the shortest path is the minimum of four linear function of arguments p and q. Let's denote them by f₁..f₄. We need to find the maximum of min{f₁, f₂, f₃, f₄} over all possible p and q. For those of you who are familiar with linear programming theory it might be obvious that to get the maximal length of the shortest path we need to check all intersection points of lines f₁ - f₂ = 0, f₁ - f₃ = 0, f₁ - f₄ = 0, f₂ - f₃ = 0, f₂ - f₄ = 0, f₃ - f₄ = 0, p = 0, p = AB, q = 0, q = CD.
For the rest of you I suggest simplier, and actually, more efficient, approach. It happens that the following pairs of paths are equal for the optimal values of p and q: p-A-C-q = p-B-D-q and p-A-D-q = p-B-C-q. This can be proved from the contrary: if this is not true we can always increase the length of the shortest path. In this case, the length of the shortest path can be found as a half of the minimum of the two following cycle lengths: p-A-C-q-D-B-p and p-A-D-q-C-D-p. See Im2Good's solution for clear implementation.
Minilek in his solution introduced another approach, that is based on two nested ternary searches to determine p and q.