Match Editorial

Match summary

In Division 1, many coders submitted solutions for the easy and medium problems very quickly. But the hard one turned out to be difficult when it received only six submissions, and none of them survived both the challenge and system test phases. Coders had to rely on their skill to challenge other coders to claim good places. At the end, with three successful challenges, tomek won the match with less than two points ahead of abikbaev, who got five successful challenges. Psyho secured the third place with fast submissions on the first two problems and a successful challenge.

Coders in Division 2, in the other hand, faced an easy 900-point problem. With fast submissions on all three problems, maksay, mRefaat, and ahm.kam_92 rounded the top three. With no challenges, they still had a safe gap of points against the other coders.

The Problems

Value	250
Submission Rate	562 / 627 (89.63%)
Success Rate	376 / 562 (66.90%)
High Score	nitdgp for 248.30 points (2 mins 21 secs)
Average Score	186.02 (for 376 correct submissions)

To solve this problem, we can use a straightforward approach which calculates the score for each number in the given range, then chooses the biggest number with the highest score. We just need to be careful when calculating the score so that no pair of numbers is counted more than once or missed out. The following Java function will return the correct score of a number:

The condition (i <= j) in line 5 ensures that no pair of numbers will be counted twice. To make the solution faster and easier to write, instead of calculating the score for one number at a time, we can sacrifice some memory to be able to calculate the scores for all numbers at the same time:

Value	600
Submission Rate	207 / 627 (33.01%)
Success Rate	87 / 207 (42.03%)
High Score	maksay for 528.35 points (10 mins 45 secs)
Average Score	329.72 (for 87 correct submissions)

Value	250
Submission Rate	463 / 491 (94.30%)
Success Rate	383 / 463 (82.72%)
High Score	blackmath for 244.24 points (4 mins 22 secs)
Average Score	188.07 (for 383 correct submissions)

This is a dynamic programming (DP) problem since:

• we can solve it by solving the similar subproblems with shorter sentences. If it is possible to translate sentence to a sequence of valid words, we can always remove the first valid word after being transformed from sentence to obtain a sub-problem with a shorter sentence.
• it is possible to memorize the results of the subproblems. If we meet a subproblem which has been solved before, it won't be computed again. Since we always remove transformed valid words from the beginning, the length of the current sentence is good enough to describe a subproblem.

The only thing left is to check if a word can be transformed to another word, and at what cost. A simple checking is to sort the letters of each word in the same order (ascending or descending in alphabet order), then compare if the two sorted words are equal. If they are equal, they can be transformed to each other. The cost can be computed by simply counting the positions where the two words differ.

tomek's solution is a good reference. The only difference between his code and the above idea is that he removed a transformed valid word from the end of the current sentence instead of from the beginning.

Value	900
Submission Rate	92 / 627 (14.67%)
Success Rate	21 / 92 (22.83%)
High Score	mRefaat for 744.04 points (13 mins 36 secs)
Average Score	523.81 (for 21 correct submissions)

Value	500
Submission Rate	365 / 491 (74.34%)
Success Rate	214 / 365 (58.63%)
High Score	ahyangyi for 477.48 points (6 mins 13 secs)
Average Score	308.71 (for 214 correct submissions)

There are several approaches to solve this problem:

Approach 1

Flood-filling by Depth-first search (DFS) or Breadth-first search (BFS) is used to count the number of pieces. The cake can be divided into many unit squares (each has a side length of 1), and a piece is a maximal connected group of unit squares which has the property that no common border (if existing) between any two squares in the group lies on a cut. So from a unit square of some piece we can visit all other unit squares belonging to that piece by limiting DFS or BFS not to cross any cut while travelling between squares. See Petr's solution for a clean implementation of this approach.

Approach 2

This approach also counts one piece at a time, but in another way. First we sort the arrays of cuts and then examine each pair of consecutive horizontal cuts horizontalCuts[i] and horizontalCuts[i+1] and each pair of consecutive vertical cuts verticalCuts[i] and verticalCuts[i+1]. Those four cuts make up a rectangle which may or may not intersect with the hole. There are few special cases:

If the rectangle is inside the hole (its sides can touch the sides of the hole), there is no piece inside that rectangle. The figures below give two examples for this case, one is completely inside the hole while the other one touches the borders of the hole:

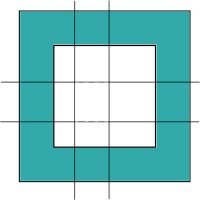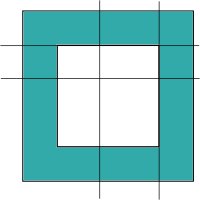If the rectangle is cut by two opposite sides of the holes, there are two pieces inside the rectangle. The pieces are highlighted in orange:

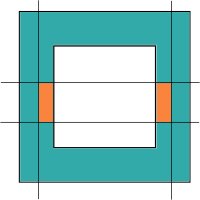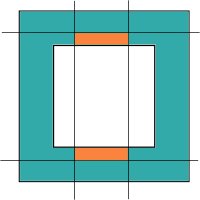In all the other cases, there will be exactly one piece inside the rectangle. So by examining all such rectangles, we can count the number of cake pieces divided by the given cuts. See abikbaev's solution for an implementation of this approach.

Approach 3

Another approach which has a smaller time complexity is to reduce the original problem to a problem with a cake and no hole. This can be done by finding two horizontal cuts:

• the horizontal cut which is inside the hole and closest to the top side of the hole. It can be the cut going through the top side of the hole.
• the horizontal cut which is inside the hole and closest to the bottom side of the hole. It can be the cut going through the bottom side of the hole.

If the two horizontal cuts of interest cannot be found, we can search for two vertical cuts with similar properties. And if, again, we cannot find the cuts, we can safely remove the hole from the original cake to obtain a reduced problem.

Solving a reduced problem is trivial. We just count the numbers of horizontal and vertical cuts which completely cut through the cake (not going through any border of the cake), add one to each number, and then multiply them together to get the number of pieces.

Value	1000
Submission Rate	6 / 491 (1.22%)
Success Rate	0 / 6 (0.00%)
High Score	No correct submissions
Average Score	No correct submissions

After reading the problem statement, our intuition tells us that this looks like a graph problem. The critical point is to find out how the graph should be constructed. If only islands are used to build the graph, it is hard to find an algorithm to work on that graph. But if both islands and seas are used, we can obtain a special graph which is easier to work on: a tree.

The tree has two types of nodes: island nodes and sea nodes. An island node can be visited only once, but a sea node can be travelled through as many times as we want. If an island connects to a sea in the map, there will be an edge connecting them in the graph. There are no edges between two islands or two seas.

Starting from any island, we use Depth-first search (DFS) to travel through the tree. At each node x, assuming that all islands of the subtree having x as the root have been optimally assigned to tours, we can calculate the status for x:

• If x is an island node, let's consider all tours assigned to the subtree:
  • If there is a tour starting at some island (not x) in the subtree and ending at x, x will have the status of 1. This tour can still be extended to end at some island outside of the subtree.
  • If there is a tour both starting and ending at x, the status of x will be 2. This tour can be extended to start and/or end at islands outside of the subtree
  • If x has been assigned to some tour which starts and ends inside the subtree, it will have the status of 0. No tour can be extended to other nodes outside of the current subtree.
• If x is a sea node, again, let's consider all tours assigned to the subtree:
  • If there is a tour starting at some island in the subtree and ending at an island node which is a direct child of x, x will have the status of 1. This tour can still be extended to the father node of x and other nodes outside of the current subtree.
  • If there is a tour which does not start or end at a direct child nodes of x, but travel through the sea represented by x, then x will have the status of 2. This tour can be easily extended to cover the father of x, but not any other nodes outside.
  • Other than the above two cases, x has the status of 0. No tour can be extended.

Using DFS we can recursively calculate the statuses for all nodes, and along the way we can determine the optimal number of tours needed. The following pseudo-code describes how it can be done: