
|
Match Editorial |
Saturday, July 19, 2008
Match summary
In both divisions, coders faced 1000-point problems that were even tougher than I'd anticipated. In Division 1, the hard problem received only two submissions, neither of which passed. In the end, the battle was between Eryx and krijgertje. Eryx was ahead after the coding phase, and towards the end of the challenge phase both had three successful challenges. Unfortunately for Eryx, his next challenge failed, leaving him just two points behind krijgertje. Al.Cash, Petr and Gluk completed the top five.
In Division 2, new-comer kmod looked strong at the end of the challenge phase, but with his hard problem failing system tests, had to settle for second place. This left snomak in first and li0n192 in third. iBob's was the only successful solution to the hard problem, but this left him with insufficient time to solve either of the others.
The Problems
ContiguousCacheEasy

Used as: Division Two - Level One:
Value 250 Submission Rate 688 / 961 (71.59%) Success Rate 560 / 688 (81.40%) High Score Valco for 235.88 points (7 mins 2 secs) Average Score 156.50 (for 560 correct submissions)
The problem describes exactly what needs to be done, so solving it is a matter of handling the details. Let's say that we have the end-points of the current range stored in P and Q, with Q = P + k - 1. When a new byte at address A is requested, we can consider three cases. In the first case, A < P, and so the new range start becomes P' = A. In the second case, A > Q, and the new range end becomes Q' = A, and hence P' = A - k + 1. Finally, if P ≤ A ≤ Q then nothing needs to be done.
If the range moves, we have to calculate how many reads are required. Let d = |P - P'| be the distance of the move. If d ≥ k then the old and the new ranges have no overlap, so k reads are required. Otherwise, d reads are required.
AddElectricalWires

Used as: Division Two - Level Two:
Used as: Division One - Level One:
Value 500 Submission Rate 258 / 961 (26.85%) Success Rate 47 / 258 (18.22%) High Score KMOD for 393.04 points (15 mins 44 secs) Average Score 260.86 (for 47 correct submissions)
Value 250 Submission Rate 607 / 645 (94.11%) Success Rate 326 / 607 (53.71%) High Score tmyklebu for 242.60 points (4 mins 59 secs) Average Score 169.39 (for 326 correct submissions)
To start with, let's assign a colour
to each mains node. We can then
colour every connected node with the same colour, for example, using a
depth-first search. Two nodes with the same colour can always be connected,
two nodes with different colours can never be connected. The only decisions
left are what to do with the nodes that currently have no colour, i.e., are
not yet connected up to the grid. If there is just one such node, it is
obviously best to connect it to all the nodes of one colour, choosing the
colour that is most common. In fact, the same applies if we there are many
such nodes, because doing so also allows us to add every missing connection
between uncoloured nodes.
See dzhulgakov's solution for an example implementation.
ClosestRegex

Used as: Division Two - Level Three:
Value 1000 Submission Rate 11 / 961 (1.14%) Success Rate 1 / 11 (9.09%) High Score iBob for 381.56 points (65 mins 18 secs) Average Score 381.56 (for 1 correct submission)
Let's consider just the first character of the text and the first atom of the regular expression (regex). If the first atom is just a character, then there is only one option: the first character of the text must match it, and if it doesn't currently, it must be changed.
Things are more interesting when the first atom is of the form x*. There are now two cases to consider: either the x* matches zero characters, and can be removed, or the first character of the text must be (or become) an x, and the rest of the text must match the original regex, including the x*.
This leads to a natural recursive approach, trying both options in each case and taking the best, but it will be too slow. Fortunately, this can easily be handled with dynamic programming. The table for DP is indexed by the length of a suffix of the text (in characters) and a suffix of the regex (in atoms).
ContiguousCache

Used as: Division One - Level Two:
Value 500 Submission Rate 259 / 645 (40.16%) Success Rate 168 / 259 (64.86%) High Score myprasanna for 452.20 points (9 mins 26 secs) Average Score 306.95 (for 168 correct submissions)
The key to this problem is to consider two types of cache moves: those that overlap the previous range and those that don't. In the former case, one will always want to move the range by the smallest amount: larger amounts may save reads later, but by at most the number of extra reads now. On the other hand, when moving to a non-overlapping range, it may be advantageous to move the range further than necessary for now, to save on reads later.
Let's start by just considering moves that always keep an overlapping range, and try to determine where to place the range for the first read. Obviously, we would like as many subsequent reads as possible to fall in this range. We can do this by tracking the highest and lowest address read, and when they fall too far apart to cover with one range, place the initial range to just cover the earlier read while being as close as possible to the later read.
What about moves that split the range? It's not always clear where to use them, since in some cases they are not required in the present but are beneficial in the future. We can attack this with dynamic programming: let dp[i] be the minimum number of reads necessary for the first i reads. To compute dp[i], we first decide how many reads fall into this block of overlap-only moves (by trying all the options). If there are r reads in the current range, then the total cost is dp[i - r] plus the cost of the current range using only overlapping moves, solved as described above. Note that we don't need, in the DP, to keep track of where the range was left at the end of the block, since we assume that the initial range for the new block will not overlap it.
krijgertje took a slightly simpler approach. He used dynamic programming, tracking the cost of doing the first i accesses and finishing with the range in position j. Normally this would be too expensive (since there are too many possible positions), but he noticed that the only useful ones are those at the very start and end of memory, and those with an end-point that is accessed by the program.
WifiPlanet

Used as: Division One - Level Three:
Value 1000 Submission Rate 2 / 645 (0.31%) Success Rate 0 / 2 (0.00%) High Score No correct submissions Average Score No correct submissions
This problem consists of two fairly separate parts. In the geometric part, one needs to break the arbitrary polygon into simpler shapes whose area can be more easily calculated. In the second, numerical part, one must determine the number of lattice points inside a simple shape.
Let's start with the geometry. One way to measure the area of a polygon to add up, for each edge, the signed area of the trapezium formed by that edge, two vertical sides and the X axis. The area of such a trapezium is 0.5(x2 - x1)(y1 + y2).
Of course, we're not interested in areas as such, we want to know how many lattice points fall within the polygon. Nevertheless, this will equal the sum of the numbers of lattice points inside each of the simple shapes (subtracting rather than adding when the area formula is negative), provided we are careful about the boundary conditions.
We can count the number of lattice points in each vertical strip and sum them up. This will give an expression of the form
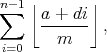
for some integers a, d and m. If either a or d lies outside the range [0, m), then the integer part can be moved outside of the floor and summed in the usual way for an arithmetic progression. Also, if d = 0, then the summation is trivial. So let us assume that both a lies in [0, m) and d in (0, m). We arrived at this expression by counting vertical strips, but with this assumption, we can also count horizontal strips, and obtain the formula (proving it is left as an exercise to the reader)
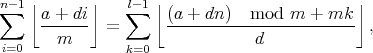
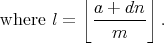
This is another expression of the original form, so you might think that we're no better off than when we started. However, we've replaced the denominator with a smaller one, in exactly the same way that the Euclidean algorithm efficiently finds the greatest common divisor. We will thus only need to perform a logarithmic number of these transformations before we find that d = 0 and we can terminate.
Exercises:
- Show how the number of lattice points within a trapezoid whose left and right edges are at x1/denom and x2/denom can be written in the form shown, with a denominator of denom(x2 - x1).
- Show how the formula you just obtained can be simplified to eliminate denom from the denominator.
- Prove the equation above.
- Prove that the equation need only be applied O(log m) times.
- How would you check that the input data are valid? Specifically, how would you check whether the boundary of the polygon passes through any lattice points?
- If you want a real challenge, try to solve the problem without the restriction that the boundary does not hit a lattice point. This is how I originally set the problem, but it is extremely difficult to ensure that each boundary lattice point is counted exactly once.
