
|
Match Editorial |
Thursday, June 5, 2008
Match summary
This match attracted 1439 competitors, 800 Div2 (117 newcomers) and 639 Div1. Div2 coders faced with usually hard Easy and Medium problem and a bit harder Hard problem. Div2 coders showed great performance in solving Medium problem and even 81.96% of submitted solutions were correct. Unfortunatelly, only two Div2 Hard solutions passed the system tests. Div1 coders faced with an easier Hard problem and a bit harder Medium problem, what can be seen by their Success Rate. Div1 coders showed great perfmormance solving Easy problem (same as Div2 Medium) - over 95% of submission were correct. Medium problem has two kind of solutions: one where you could use some data structure and optimized it and in some cases risk will it run 1.99 or 2.01 seconds for some test cases - something like that happened to syco; or to find algorithm that don't use any data structure and with high time margin passes the system tests.
At first glance, it seems that Div1 Easy will trouble coders - i.e. a lot of red coders haven't so fast submission on this task as they usually have; one of them, crazyb0y, resubmitted his solution. bmerry first submitted Medium problem solution and that was the fastest solution of all. Before challange phase started, first 5 positions in Div1 were JongMan, rem, Petr, bmerry and yuhch123. At the beggining of challenge phase coders were focused on Medium problem and it showed as good decision. Challenge phase made some changes in top three positions moving bmerry on the second place. System testing phase made final list. Without any challenge made at all JongMan won the match, folowed by bmerry who thanks to 125 points earned in challenge phase need only 2 points more to won the match. Third place took rem who continue showing his great success and became target - congrats rem! yuhch123 and RAVEman took fourth and fifth place respectively.
In Div2, before the Challange phase started, newcomers ILoveChenDanqi and SergeiFedorov were on the second and third place respectively, and tripleCross was on the first place. Challenge phase and System testing phase was too cruel to top 3 coders and changed the top 3 places at all. leehark won the match with over 100 points margin, folowed by ngg who earned 50 points in Challange phase. Third place took mitsiddharth who won 100 points in the Challange phase. Forth and fifth place went to newcomers UranusX and ILoveChenDanqi respectively.
Note that after this match there are even 15 targets!
The Problems
ReadingBooks

Used as: Division Two - Level One:
Value 250 Submission Rate 610 / 789 (77.31%) Success Rate 345 / 610 (56.56%) High Score SheynHu for 247.31 points (2 mins 58 secs) Average Score 167.89 (for 345 correct submissions)
This problem was a classical greedy one. If you carefully solve the examples, you will notice
that starting form the first part of input each time you find 3 different consecutive
parts (that means you can read the whole book) take it as one book, increment you result and
go on from the last choosen part.
Let's proove that algorithm is correct.
Suppose there is some set book1 of three different
parts (i.e. "story", "introduction", "eidification") that shouldn't be considered as one book
in order to get the optimal solution. Consider next set book2 that contains three different
parts, but such set that first appears after book1 and it is part of the optimal solution.
In that case there are two options:
- book1 and book2 do not overlap. We will make this part of proof by
contradiction.
If parts that appear in book1 are completely removed, it will not affect the optimal solution. In that case, there is one book more that can be read completely (that is book1), so the optimal solution can be increased, what is contradiction that the solution without book1 is optimal one. -
book1 and book2 overlap. We will show that it doesn't matter whether you
choose book1 or book2.
Take together all part from the both sets. There will be at most 5 parts. With those 5 parts you can include exactly one book more in the final result - (book2 and book1 gives at least one book, but for more than one book you need at least 6 parts, so there is no way to have two or more books). But choosing book1 instead book2 will not change the rest of optimal solution, because book1 appears before book2. Also, chossing book1 will disable to choose book2 and vice versa (so whatever you choose, you will be able to choose only one book), what means that choosing book1 instead book2 doesn't affect the optimal solution at all.
public int countBooks(String[] readParts){
int ret = 0;
int mask[] = new int[readParts.length];
for (int i = 0; i < readParts.length; i++)
if (readParts[i].equals("introduction"))
mask[i] = 1;
else if (readParts[i].equals("story"))
mask[i] = 2;
else
mask[i] = 4;
for (int i = 2; i < readParts.length; i++)
if ((mask[i] | mask[i - 1] | mask[i - 2]) == 7){
ret++;
i += 2;
}
return ret;
}Homework
- Try to solve the task when parts have to be read in given order (i.e. first introduction, then story, then edification, so ("introduction", "edification", "story") can't be parts of one book - result 0, but ("introduction", "story", "edification") could be - result 1).


Used as: Division Two - Level Two:
Used as: Division One - Level One:
Value 500 Submission Rate 381 / 789 (48.29%) Success Rate 314 / 381 (82.41%) High Score Hanaban for 466.80 points (7 mins 41 secs) Average Score 304.28 (for 314 correct submissions)
Value 250 Submission Rate 617 / 637 (96.86%) Success Rate 594 / 617 (96.27%) High Score tourist for 246.89 points (3 mins 11 secs) Average Score 198.68 (for 594 correct submissions)
This problem was fairly clear and easy to understand. So detailed descrpition of the example 0
gave almost complete algorithm of the solution. But let us explain the solution completely.
First of all, if you are given such configuration as it was given in the problem,
there always exists unique solution.
First step is to show if are known two neighbour digits (one in the same row and
in the row below), than third can be determined uniquely. Let a and c be known
and b unknown digit. Then
(a+b) MOD 10=c; 0≤a,b,c≤9
- if a>c => a+b-10=c => b=c+10-a
- if a<=c => a+b=c => b=c-a
elements on the left side: using k-th element and an element from the row r determine the k-1-th element; using the element k-1 and corresponding element form the row r determine the element k-2 and so on, until the first element is reached.
elements on the right side: for this side is almost same as for the elements on the left side, just start revealing the element k+1, then the element k+2 and so on, until the last element is reached.
At the begging all digits are uniquely determined (it is part of the problem). Using the idea that explain us how to determine third neighbour if two of them are known, a new digit is always uniquely determined, so the whole triangle is uniquely determined.
Below is code written in Java that folows explained solution
public String[] calcTriangle(String[] questionMarkTriangle){
String[] ret = questionMarkTriangle;
int n = ret.length;
if (n == 1)
return ret;
int pos[] = new int[n];
char cc[][] = new char[n][n];
for (int i = 0; i < n; i++)
for (int j = 0; j < ret[i].length(); j++){
cc[i][j] = ret[i].charAt(j);
if (cc[i][j] != '?')
pos[i] = j;
}
// go through questionMarkTriangle and restore values
for (int i = n - 2; i > -1; i--){
for (int j = pos[i] + 1; j < n - i; j++)
cc[i][j] = (char)((cc[i + 1][j - 1] - cc[i][j - 1] + 10) % 10 + 48);
for (int j = pos[i] - 1; j > -1; j--)
cc[i][j] = (char)((cc[i + 1][j] - cc[i][j + 1] + 10) % 10 + 48);
}
for (int i = 0; i < n; i++)
ret[i] = new String(cc[i], 0, ret[i].length());
return ret;
}Homework
-
Try to solve the problem where you are given
int[] valandint[] pos, where(pos[i], val[i])means in thei-th rowpos[i]-th element isval[i], but others in that row are unknown.val[i]fits into 16-bit integer.


Used as: Division Two - Level Three:
Value 1000 Submission Rate 17 / 789 (2.15%) Success Rate 2 / 17 (11.76%) High Score leehark for 505.17 points (36 mins 50 secs) Average Score 500.48 (for 2 correct submissions)
This problem is a dynamic programming problem. Part of the problem involves using math to
find out whether John can jump from one stair to another stair. First, we will examine the "math
part".
Suppose there are two stairs st1 and st2, given by positions of its left
endpoints (st1.x, st1.y) and (st2.x, st2.y) and by its length
st1.len and st2.len. We will suppose that st1.y < st2.y.
Consider two cases:
- (st1.x<=st2.x and st2.x<=st1.x+st1.len) or
(st2.x<=st1.x and st1.x<=st2.x+st2.len) (**)- like
on the picture presented below
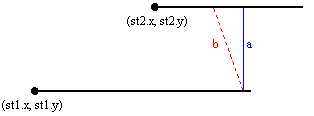
It is obvioulsy that for each segment b (red-dotted segment on the picture) its length is always greater or equal to the length of the segment a (blue-filled segment on the picture). So, in this case, the shortest distance between these stairs is just st1.y-st2.y and if that value is smaller or equal to K, st2 is reachable from st1. - else (The previous condition (**) is not satisfied) - one possibility is
presented on the picture below
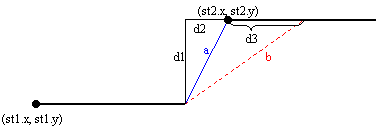
Let us calculate a distance between some point of st1 (on the picture it is the endpoint) and some point of st2 (on the picture the length b).
b^2 = (d2 + d3)^2 + d1^2 = d2^2 + 2*d2*d3 + d3^2 + d1^2 = d1^2 + d2^2 + 2*d2*d3 + d3^2 ≥ a^2, that means b > a. So, in this case, when we fix point on one stair, the smallest difference between that point and another stair is along the segment that is connected to the endpoint of the second stair. Final conclusion is that the shortest distance have to be founded between stairs' endpoints. If the shortest of all such distances is smaller or equal to K, then st2 is reachable from the stair st1.
int sqr(int val){
return val * val;
}
boolean reachable(int idx1, int idx2){
// the first case
if ((stair[idx1].x <= stair[idx2].x && stair[idx2].x <= stair[idx1].x + stair[idx1].len) ||
(stair[idx2].x <= stair[idx1].x && stair[idx1].x <= stair[idx2].x + stair[idx2].len))
return Math.abs(stair[idx1].y - stair[idx2].y) <= K;
// the second case
return (sqr(stair[idx2].x - stair[idx1].x - stair[idx1].len) +
sqr(stair[idx2].y - stair[idx1].y) <= sqr(K)) || (sqr(stair[idx1].x -
stair[idx2].x - stair[idx2].len) + sqr(stair[idx1].y - stair[idx2].y) <= sqr(K));
}
Let
dp[i] be the highest number of sweets that John can collect starting
his "jump-journey" from the stair i. We will consider that stairs st1,
st2, ..., stk are in the same group iff for each stair all others are reachable -
actually, that are all reachable stairs wit same y-coordinate. Note that when John is positioned
on some stair, he should collect all sweets within the current group of stairs, because
he can visit all stairs of some group and get back to the stair from which he started visiting to
decide what next :)We explained what should be done with stairs within the same group, John can't move down, so next what he can done is to go up. John can move wherever he wants inside the group, that menas from one stair inside the group he can get to each stair that is reachable from any stair from the group. His next jump to some stair
next reachable from the group had to be choosen in
such way that dp[next] is maximal.When
dp value is calculated for each stair, return that one with maximal value.
Below is commented code in Java that should help to reader to understand the idea of the algorithm.
private class Stair implements Comparable{
int x, y, len, sw;
Stair(int x, int y, int len, int sw){
this.x = x;
this.y = y;
this.len = len;
this.sw = sw;
}
public int compareTo(Object stairo){
Stair stair = (Stair)(stairo);
if (y < stair.y)
return -1;
else if (y > stair.y)
return 1;
else{
if (x < stair.x)
return -1;
else
return 1;
}
}
}
Stair stair[];
int n, K;
int dp[];
int memo(int idx){
// if it is already calculated, return it
if (dp[idx] != -1)
return dp[idx];
// sum sweets that are reachable from current stair and they are placed on same y line
int sum = stair[idx].sw, st1, st2, i;
for (i = idx - 1; i > -1; i--)
if ((stair[i].y == stair[i + 1].y) && reachable(i, i + 1))
sum += stair[i].sw;
else
break;
st1 = i + 1;
for (i = idx + 1; i < n; i++)
if ((stair[i].y == stair[i - 1].y) && reachable(i, i - 1))
sum += stair[i].sw;
else
break;
st2 = i - 1;
// now we have the sum. let's go through all stairs and try to jump on any reachable
dp[idx] = 0;
for (i = 0; i < n; i++)
// try reachable stairs
if (i != idx && stair[i].y >= stair[idx].y && reachable(i, idx)){
if (stair[i].y == stair[idx].y)
dp[idx] = Math.max(dp[idx], memo(i));
else
dp[idx] = Math.max(dp[idx], memo(i) + sum);
}
// now we should update stairs optimal solutions
// suppose for some group of reachable stairs with the same y-coord, optimal solution
// exists for stair with index idx. if we move left from idx to check stair on the same line
// then we can't move from idx-1 to idx (note that dp[idx] = 0 in that time - if it is not, we
// could get infinite recursion), but we should update dp[idx-1] to dp[idx] later
for (i = st1; i <= st2; i++){
// don't update stair that wasn't visited yet, because latter you
// won't be able to examine that
if (dp[i] == -1)
memo(i);
dp[i] = Math.max(dp[i], dp[idx]);
}
// if can't reach any stair, then maximum is collected sweets on the y-coord
dp[idx] = Math.max(dp[idx], sum);
return dp[idx];
}
int collectSweets(int K, int[] sweets,
int[] x, int[] y, int[] stairLength){
this.K = K;
n = sweets.length;
dp = new int[n];
Arrays.fill(dp, -1);
stair = new Stair[n];
for (int i = 0; i < n; i++)
stair[i] = new Stair(x[i], y[i], stairLength[i], sweets[i]);
Arrays.sort(stair);
int ret = 0;
for (int i = 0; i < n; i++)
if (stair[i].y <= K)
// for each stair, check if John starting from
// it can collect maximum number of sweets.
ret = Math.max(memo(i), ret);
return ret;
}Alternative solution:
Let us remind about groups of stairs. We didn't mention that if some stair from a first group can reach some stair from a second group, then from each stair from the first group there is jump-path that reaches any stair in the second group - in this case we will say the first group can reach the second. This is possible because all stairs within same group are jump-reachable. Let us make a short description what we was doing in our algorithm: start with some group; visit all stairs within that group; reach next group and continue with same steps. So much times group that I would like to change it into something another - what about graph :) Seriously, if group is represented as node, then two groups can be connected or not - reason behind this was just explained. Moving from stair to stair is same as moving from group to group. Modeling the problem as graph where each node has cost, the cost is actually sum of sweets in the group, we get topological graph and problem is to find path with highest sum respect to costs of the nodes.
Below is code for this kind of solution.
int numg;
boolean g[][];
int sumg[], markg[], yg[];
int ret;
int dfs(int v){
if (dp[v] != -1)
return dp[v];
int ret = sumg[v];
for (int i = 0; i < numg; i++)
if (g[v][i])
ret = Math.max(ret, dfs(i) + sumg[v]);
return dp[v] = ret;
}
public int collectSweets(int K, int[] sweets, int[] x, int[] y, int[] stairLength){
this.K = K;
n = sweets.length;
dp = new int[n];
Arrays.fill(dp, -1);
stair = new Stair[n];
for (int i = 0; i < n; i++)
stair[i] = new Stair(x[i], y[i], stairLength[i], sweets[i]);
Arrays.sort(stair);
sumg = new int[50];
markg = new int[50];
yg = new int[50];
numg = 0;
// count number of groups
for (int i = 0; i < stair.length; ){
int j = i + 1, sum = stair[i].sw;
markg[i] = numg;
while (j < stair.length && stair[j].y == stair[i].y && reachable(j - 1, j)){
sum += stair[j].sw;
// mark j as part of the group numg
markg[j] = numg;
j++;
}
// number of sweets in the group numg
sumg[numg] = sum;
yg[numg] = stair[i].y;
i = j;
numg++;
}
g = new boolean[numg][numg];
for (int i = 0; i < numg; i++)
Arrays.fill(g[i], false);
// make graph
for (int i = 0; i < stair.length; i++)
for (int j = i + 1; j < stair.length; j++)
if (markg[i] != markg[j])
if (reachable(i, j))
g[markg[i]][markg[j]] = true;
// we got topological graph, run DFS
Arrays.fill(dp, -1);
int ret = 0;
for (int i = 0; i < numg; i++)
if (yg[i] <= K)
ret = Math.max(ret, dfs(i));
return ret;
}Homework
-
Try to solve task if John is not able to make more than
maxJumpjumps.


Used as: Division One - Level Two:
Value 500 Submission Rate 286 / 637 (44.90%) Success Rate 104 / 286 (36.36%) High Score bmerry for 446.94 points (10 mins 2 secs) Average Score 301.47 (for 104 correct submissions)
This problem was a bit harder than usual Medium Div1 problem. We will show three
aproaches, but only one that surely will not TLE.
First approach
For each k (just to remind, k is a length of subsequence)
compare all subsequnces. This runs in O(n^3) what is of course too slow to pass
for 2 sec.
Second approach
For each k calc all sums and remember their indexes. Sort all sums.
Go through all sums from the smallest one. Also provide your algorithm with
segment/interval tree where you will be able to find maximal element in logarithmic time
within some interval. Let us explain how a sum should be added to interval tree.
Consider sum s(i, k) = val(i). i is remembered before sorting
so it is still presented, val(i) is sum and k is the length of
the subsequence. s(i, k) should be stored in tree as the value of i-th
leaf. We also should use tree to find what is minimal difference with current sum and
already processed sums. In order to done that, find maximal value in tree in interval
[0, i) and [i + k, n) - sums with indexes [i, i + k)
will overlap with the current one.
Time complexity of this algorithm is O(n^2 log n) with a "high" constant, so it
is quite risky, we are not sure will it pass within 2 sec. - probably will not for the worst test case.
Third approach
Lemma 1:
If there exists two sums s(i, k) and s(j, k), (i < j), with
difference dif and they overlap, then there exists sums s(i1, k1)
and s(j1, k1) that have the same difference and do not overlap.
Proof.
s(i, k) and s(j, k) can be written as
s(i, k) = ai + ai+1 + ... + ai+k-1, and
s(j, k) = aj + aj+1 + ... + aj+k-1.
Because they overlap, there must exists some p such that ap
belongs to s(i, j) and s(j, k). But
i < j, j ≤ p => j belongs to the intersection part
i < j => i+k-1 < j+k-1, finally we can conclude that
elements aj, aj+1, ..., ai+k-1 belong
to the intersection part (ilustrated on the picture below).

Rewrite that difference as
s(i, k) - s(j, k) = (ai + ai+1 + ... + aj-1 +
aj + ... + ai+k-1) -
(aj + aj+1 + ... + ai+k-1 + ai+k +
... + aj+k-1) =
(ai + ai+1 + ... + aj-1) -
(ai+k + ai+k+1 + ... + aj+k-1) = s(i, j-i) - s(i+k, j-i).
So,
s(i, k) - s(j, k) = s(i, j-i) - s(i+k, j-i).As in the Second approach we are looking for the minimal difference for each possible
k starting with the smallest one.
To find the smallest difference between two subsequence, we will sort all sums and
consider only neighbour sorted sums. It is already explained in
editorial
for SRM 398 Div2 Easy problem why we can sort elements in order to find the minimal difference.
Lemma 1 guarantee that if we compare two elements that have minimal difference,
but they overlap, then we also found the same difference between two sums that didn't overlap.
Algorithm could be divided into two parts whether minimal difference reached 0 or not.
- If the minimal difference didn't reach 0 yet, we just should compare two neighbour sorted sums as it was explained above.
-
If the minimal difference is 0, then within the sorted sums we only should check
if there exist subsequnces with the same sum values - we need this in order to update
kthat should be returned. But now, if for each sum value we check with all others to find out whether it overlap or not, our algorithm could become too slow. The trick is to find minimal and maximal index of all sums with a same sum value and check whether they overlap or not; or we can sort sums by sum and indexes (as it was done in the solution below).
private class Sum implements Comparable{
int idx;
long val;
Sum(long val, int idx){
this.val = val;
this.idx = idx;
}
public int compareTo(Object sumo){
Sum sum = (Sum)(sumo);
if (val < sum.val)
return -1;
else if (val == sum.val){
if (idx < sum.idx)
return -1;
else if (idx == sum.idx)
return 0;
else
return 1;
}
else
return 1;
}
}
int[] maxSubstring(int A0, int X, int Y, int M, int n){
long A[] = new long[n];
long ss[] = new long[n + 1];
ss[0] = 0;
ss[1] = A0;
A[0] = A0;
for (int i = 1; i < n; i++){
A[i] = ((A[i - 1] * (long)(X) + (long)(Y)) % (long)(M));
ss[i + 1] = ss[i] + A[i];
}
int retlen = 1 << 20, i, j, slen;
long val = 1L << 60L, sum;
Sum s[] = new Sum[n];
slen = n + 1;
for (int len = 1; 2 * len <= n; len++){
slen--;
for (i = 0; i < slen; i++)
s[i] = new Sum(ss[i + len] - ss[i], i);
Arrays.sort(s, 0, slen);
if (val > 0)
for (i = 0; i < slen - 1; i++){
// try to update return values if subsequences do not overlap
if (s[i + 1].val - s[i].val <= val &&
Math.min(s[i + 1].idx, s[i].idx) + len <= Math.max(s[i + 1].idx, s[i].idx)){
val = s[i + 1].val - s[i].val;
retlen = len;
}
}
else{
// sorted array is something like a..ab...bc..cd..d.... and we find
// max and min index in each x..x - they are sorted, so we should find the index
// of the leftomost and the rightmost x
i = 0;
while (i < slen){
j = i + 1;
while (j < slen && s[j].val == s[i].val)
j++;
if (s[i].idx + len <= s[j - 1].idx)
retlen = len;
i = j;
}
}
}
int ret[] = new int[2];
ret[0] = retlen;
ret[1] = (int)(val);
return ret;
}As a references on a different solutions, you can take a look at HiltonLange's solution, at KOTEHOK's solution or bmerry's solution
Homework
-
Try to solve task if in case there are more solutions with same difference and
k, return that one with a highest difference between minimal elements of the resulting subsequences. -
Try to solve task if in case of tie difference with the smallest
kshould be returned. -
Is it important if we instead starting with the smallest
k, start with the highest, but everything is still same in the algorithm (just change definitionforloop)? If it is not same, then why?


Used as: Division One - Level Three:
Value 950 Submission Rate 86 / 637 (13.50%) Success Rate 43 / 86 (50.00%) High Score JongMan for 776.23 points (14 mins 6 secs) Average Score 520.30 (for 43 correct submissions)
This problem wasn't so hard (that is the reason why it worth 950 points). It involves knowledge about max-flow graph theory and careful coding just to avoid possible mistakes when there is part about "tricky" examples. Here will not be explained the algorithm for max-flow, because it is already explained in tutorial Maximum Flow by _efer_. The point of this editorial is to explain how graph should be constructed. Take a look at the picture below.
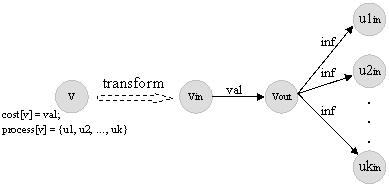
Once you make a graph, push infinite flow through source node (the node given by company1) and calc how much will get to the sink node (the node given by company2). You can push infinite flow through source node because statement says it, but do not worry, maximal (producing) capacity of the sink company is limited by amount. Statement just says that you can consider that company1 is provided with enough data.
To return a final list, go through all possible sets of companies, find set such that using its companies gives maximal possible flow which cost is minimal of all maximal flows and if there are more max-flow min-cost sets, return the one lexicographically smallest.
You can take a look at rem's solution.
