
|
Match Editorial |
Saturday, November 17, 2007
AlmostPrimeNumbers
The key part of this problem is to determine whether an integer number is almost prime or not.
According to the definition, it shouldn't be prime and divisible by numbers less than 11.
So, the Java function looks like this:
boolean isAlmostPrime(int n) {
return !isPrime(n) && n%2 !=0 && n%3 !=0 && n%5 !=0 && n%7 !=0;
}
Having this function, we just iterate through all the numbers that are greater than the given one and
return the first almost prime number found. The only thing left to discuss is how long can we search for
the smallest almost prime number that is greater than the given one. This is not very easy question, but
it's good we need not to make a complex analysis. It's obvious that all powers of 11 are almost prime,
and 11^6 = 1771561. So, even this raw estimation shows that our code will not timeout, if we implement the function
isPrime to work in O(sqrt(n)). If you don't know how to do that, please read
this tutorial.
SquaresInsideLattice
The key observation in this problem is: for each square inside the lattice its bounding box is a square too. By bounding box we mean the smallest rectangle with sides parallel to the axes, which contains the given square. So, each square with sides parallel to the axes uniquely defines some number of lattice squares. And this number depends only on the size of the square, actually it equals to the length of the square's side. So, all we need is to iterate through all possible lengths of square's side and count the answer. Here is a Java implementation of this approach:
long res = 0;
for (long i = 1; i <= Math.min(width,height); ++i)
res += (width - i + 1) * (height - i + 1) * i;
GameOnAGraph
This problem was yet another exercise with the matrices. To see this let's look what happens with the vertices' marks during the game. Let's denote the marks before some turn as x1, x2, ..., xn and after that turn as y1, y2, ..., yn. Then we can write the following equations:
y1 = A1,1x1 + A1,2x2 + ... + A1,nxn y2 = A2,1x1 + A2,2x2 + ... + A2,nxn ................................. yn = An,1x1 + An,2x2 + ... + An,nxnHere coefficients Ai,j depend on the graph and whether the turn was white or black. These linear equations can be written using matrices in a compact form as: Y = A*X. Where X and Y are columns and A is a square matrix of coefficients. As we can see matrix A doesn't depend on the initial marks. Let's denote by W and B matrices which correspond to white and black turns respectively and by X the column of initial marks. Then, after the first turn marks will be W*X, after the second turn B*W*X, then W*B*W*X and so on... Since the matrix multiplication is an associative operation we get the following solution (in pseudo code):
solve(Graph g, int N, Column X){
Find Matrix W (depends on g)
Find Matrix B (depends on g)
C := ( B*W )^( N/2 )
if (N is odd) C := W*C
return C*X
}
Among other things you should implement matrix multiplication and exponentiation. The later must be done such that the number of multiplications
is proportional to log(N) to work fast enough.
Please, read this if you are not familiar with the logarithmic exponentiation.
AlienLanguage
This problem has many solutions. We'll describe some of them. But first, let's figure out what we should find. Let our word contains V vowels and C consonants. Then we have exactly P^V*Q^C words, not counting stresses. With stresses each of these words will define 1 + V + C + V*C = (V+1)*(C+1) different words. So, the answer to the problem is (-1 because we don't allow empty words):
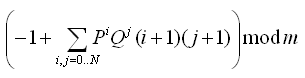
This form is not very convinient, so let's rewrite it like this:
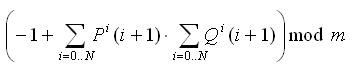
Now we see that we only need to know how to compute the sum S(n) = 1 + 2*x + 3*x^2 + ... + (n+1)*x^n. This is the crotch where different solutions actually start to differ.
Method 1: Recurrence
We can notice that for odd n (n = 2*k-1) the following is true:
S( 2*k-1 ) = ( 1 + x^k )*S( k-1 ) + k*x^k*( 1+x+x^2+...+x^(k-1) ),
or if we denote the sum of
geometrical progression 1+x+x^2+...+x^k by G(k), then
S( 2*k-1 ) = ( 1 + x^k )*S( k-1 ) + k*x^k*G( k-1 ).
This means that we have a recurrence which decreases the power by 2. So, we can compute the result in logarithmic time.
But to do that we must be able to count G(k) which is not very hard because of the similar recurrence:
G(2*k-1) = ( 1 + x^k )*G( k-1 ).
Method 2: Matrices
It turns out that matrices are applicable in this problem too. Let's see how.
We can write the following equations:
S( n+1 ) = x * S( n ) + x * G( n ) + 1 G( n+1 ) = 0 + x * G( n ) + 1 1 = 0 + 0 + 1Now, it's clear where the matrices came from. Specifically,
( S( n+1 ) ) ( x x 1 ) ( S( n ) ) ( G( n+1 ) ) = ( 0 x 1 ) ( G( n ) ) ( 1 ) ( 0 0 1 ) ( 1 )So, all we need is to find a corresponding power of the given 3x3 matrix. Of cource, it should be fast to pass the system tests. Fortunately, we already know how to do this from the previous problem.
Method 3: Closed form
Another way to solve this problem is to find a formula.
We already know that S( n ) = x*S( n-1 ) + G( n ), but on the other hand S( n ) = S( n-1 ) + (n+1)*x^n. Getting rid of S( n-1 ) we
yield that S( n ) = ( (n+1)*x^(n+2) - (n+2)*x^(n+1) + 1 ) / (x-1)^2
Although division is a problem for modular computation, it can be resolved in the following way: we need to count numerator by modulo M*(x-1)^2 instead
of M and after that divide it by (x-1)^2.
