
|
Match Editorial |
Tuesday, October 2, 2007
Match summary
After my previous sets of rather hard Division 2 problems I decided to try sharing a problem as the Div1 easy and Div2 hard. The experiment proved to be quite successful and led to a reasonably hard Division 2 problem set. Twenty-two coders were able to finish all three problems, and between them speed and successful challenges mattered.
Thanks to five successful challenges ryuwonha took the first place with a comfortable lead of over 200 points. A newcomer Ted was second and relatko third.
Division 1 had a harder time, with a medium problem that required some knowledge of geometry and a tough hard problem from coding theory. Five minutes before the end there were only a few submissions on the hard problem, and most of them were obviously wrong. As usual, we got more submissions during the last minutes, but the challenge phase was efficient and the system tests merciless. In the end, only cnettel's solution survived all the tests (including three challenges), and gave him a reason to be proud.
However, solving the hard problem was not enough to win the match. An obvious candidate for match victory was bmerry with his fastest times both on the easy and on the medium problem. But this time he had to settle for second place -- nya discovered how tricky the easy problem is, and with eight successful challenges beat bmerry (and his "only" five successful challenges) by mere two points. The third place went to gawry, who became a target after this match.
Usage notes
This editorial is suitable for people of all ages, races and genders. Recommended daily usage: stop before your head starts to hurt. The text comes with free exercises, feel free to discuss them in the forums.
The Problems
PirateTreasure

Used as: Division Two - Level One:
Value 300 Submission Rate 505 / 625 (80.80%) Success Rate 448 / 505 (88.71%) High Score FrancaiS for 297.13 points (2 mins 47 secs) Average Score 216.74 (for 448 correct submissions)
We will imagine a coordinate system in the plane of the island, with the x axis pointing east and the y axis pointing north. Now moves north, south, east and west correspond to moves by [0,+1], [0,-1], [+1,0], and [-1,0]. The hardest part in solving this task was to compute how do the moves in the other four directions change our coordinates.
Here we can use the theorem of Pythagoras. Say that we make a move "X steps northeast". Its equivalent is moving Y steps north and the same amount east, for some unknown (not necessarily integer) value Y. How to compute Y?
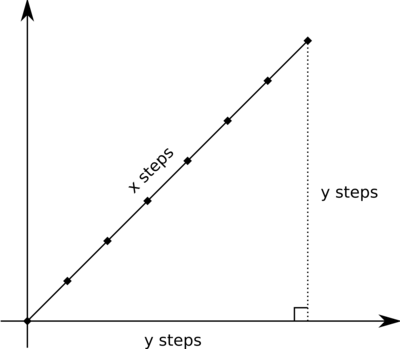
The situation can be drawn as a right triangle where the hypotenuse has length X and both legs have length Y, just as in the picture above. From Pythagoras's theorem we get the equation Y2 + Y2 = X2. This can be simplified to 2Y2 = X2. Both sides of the equation are positive, thus we can compute their square roots and they have to be equal. We get Y√2 = X.
That can be rewritten to Y = X/√2. Another form of the same expression is Y = X√2/2. (We can obtain it by multiplying both the numerator and the denumerator of X/√2 by √2.) Thus the move "X steps northeast" is the same as "X√2/2 steps north, X√2/2 steps west".
One more thing: instead of having the same code eight times (once for each direction), it is much more convenient and less error prone to enter the directions as constants, and then to use loops. Our code that uses this approach follows.
public final class PirateTreasure {
double sq2 = Math.sqrt(2.0) / 2.0;
String[] DIR = {"NORTH","SOUTH","EAST","WEST",
"NORTHWEST","NORTHEAST","SOUTHWEST","SOUTHEAST"};
double[] dx = { 0, 0, 1, -1, -sq2, sq2, -sq2, sq2};
double[] dy = { 1, -1, 0, 0, sq2, sq2, -sq2, -sq2};
// going in the direction DIR[i] corresponds to moving by +dx[i],+dy[i]
public double getDistance (int[] steps, String[] directions) {
double x=0, y=0;
for (int i=0; i<steps.length; i++) {
int d=0;
while (!directions[i].equals(DIR[d])) d++;
x += dx[d] * steps[i];
y += dy[d] * steps[i];
}
return Math.sqrt(x*x+y*y);
}
}
Exercises
- 1.1 Suppose that you are allowed to ignore some of the directions. Design a polynomial algorithm that will compute at most how far from the initial location can you get.
- 1.2 Solve a variation of the original task where directions are given in degrees instead of compass directions. (Hint: sine and cosine will be your friends.)
- 1.3 In this setting (arbitrary directions), can you still solve the same task as in 1.1?


Used as: Division Two - Level Two:
Value 500 Submission Rate 253 / 625 (40.48%) Success Rate 224 / 253 (88.54%) High Score ryuwonha for 489.88 points (4 mins 5 secs) Average Score 345.17 (for 224 correct submissions)
First of all, note that the order in which we flip the switches does not matter. And flipping a switch twice is obviously the same as not flipping it at all. Thus all we need to do is to find the smallest set of switches we have to flip.
Consider the bulb in the lower right corner. There is only one switch that affects this bulb. If this bulb is currently off, we have to flip that switch.
Now consider the bulb to the left of it. There are only two switches that affect it, and for one of them we already decided whether to flip it or not. If the bulb is currently off, we have to flip the other switch.
We can continue in this way until we set all the switches in the bottom row correctly. Now we can move on to the next row (again, starting from the right), and so on, until we process the entire board.
Obviously, this process will always lead to all bulbs being on at the end. Also, all the flips we made were necessary -- if we omit any of them, we can find a bulb that won't be on. Thus their count is optimal.
A straightforward implementation of this approach leads to the following O(R2C2) algorithm:
int solveSlow(String[] B) {
int R = B.length, C = B[0].length();
boolean[][] on = new boolean[R][C];
for (int r=0; r<R; r++) for (int c=0; c<C; c++) on[r][c] = (B[r].charAt(c)=='1');
int res = 0;
for (int r=R-1; r>=0; r--) for (int c=C-1; c>=0; c--) if (!on[r][c]) {
// if this bulb is off, we have to flip the corresponding rectangle
for (int x=0; x<=r; x++) for (int y=0; y<=c; y++) on[x][y] = !on[x][y];
res++;
}
return res;
}
Exercises
- 2.1 There is an O(RC) algorithm for this task. Find one.
- 2.2 Is it possible to design a real board with bulbs and switches that would behave like the one in the problem statement? How/why?
- 2.3 Write a formal proof of the statement "for each final state of the board there is exactly one combination of switches that produces it".


Used as: Division Two - Level Three:
Used as: Division One - Level One:
Value 900 Submission Rate 192 / 625 (30.72%) Success Rate 33 / 192 (17.19%) High Score kemo for 796.92 points (10 mins 29 secs) Average Score 544.97 (for 33 correct submissions)
Value 250 Submission Rate 495 / 523 (94.65%) Success Rate 174 / 495 (35.15%) High Score bmerry for 243.16 points (4 mins 47 secs) Average Score 178.54 (for 174 correct submissions)
We'll start with one definition: Let C be a cell that contains a number. If it is allowed to move the token from C to some other cell D, we will call D the child of C.
A slower solution
One possible way of approaching the problem is almost deceptively simple. Given a cell, what is the maximum number of moves we can make starting in this cell? If the cell is a hole (or outside the board), the answer is clearly zero. If it is a number, the answer is one larger than the maximum of the answers for its children.
Of course, the board may contain cycles. In that case, if we can reach a cycle from a cell, the answer for this cell will be ∞.
One way how to solve the task was simply to iterate through all the cells, and for each of them check whether we can already compute the answer. Repeat this process until you encounter an iteration where you can compute no new information. At this moment you can safely conclude that for all cells that are still unknown the answer is ∞.
(A sketch of a proof why this really works: Prove by induction that if an answer for a cell is a finite integer X, then you will compute this in the X-th iteration or earlier. The induction step works because all children of this cell must have finite answers that are less than X.)
String[] B; // the board
int R,C; // the number of rows and cols on the board
int[] dr={-1,1,0,0}, dc={0,0,-1,1};
int solveUsingIterations() {
// initialize best to 0 for holes / -1 for unknown
int[][] best = new int[R][C];
for (int r=0; r<R; r++) for (int c=0; c<C; c++)
if (B[r].charAt(c)=='H') best[r][c]=0; else best[r][c]=-1;
for (int loop=0; loop<R*C+10; loop++) {
// iterate through the board and try to compute new information
for (int r=0; r<R; r++) for (int c=0; c<C; c++) {
if (best[r][c]>=0) continue;
int mx=0, ok=1, jumpLength=B[r].charAt(c)-48;
for (int d=0; d<4; d++) {
int nr=r+jumpLength*dr[d], nc=c+jumpLength*dc[d];
if (nr<0 || nr>=R || nc<0 || nc>=C) {
mx = Math.max(mx,1);
} else {
if (B[nr].charAt(nc)=='H') {
mx = Math.max(mx,1);
} else {
if (best[nr][nc]==-1) ok=0; else mx = Math.max(mx,best[nr][nc]+1);
}
}
}
if (ok==1) best[r][c]=mx;
}
}
return best[0][0];
}
Note that in our code we use a fixed number of iterations. We can do this because no finite answer can be larger than RC -- any path without cycles can only visit each of the cells at most once.
The time complexity of this solution is O(R2C2).
A faster solution
Instead of applying the "one plus maximum of answers for all children" formula on all cells over and over again, we can try to compute it only for the cells where it really matters.
We can easily rewrite the formula into a recursive solution:
int getResult(int r, int c) {
if (r<0 || r>=R || c<0 || c>=C) return 0;
int res = 0;
int jumpLength=B[r].charAt(c)-48;
for (int d=0; d<4; d++)
res = Math.max(res, 1+getResult( r+jumpLength*dr[d], c+jumpLength*dc[d] ) );
return res;
}
This code still has two problems. The first problem is that it tries all possible paths. For inputs like the one below the number of paths grows exponentially when we increase the input size. This would cause the solution to exceed the time limit.
12H12H12H12H12H 2H12H12H12H12H1 H12H12H12H12H12 12H12H12H12H12H 2H12H12H12H12H1 H12H12H12H12H12
This illness can be cured using simple memoization: Once we compute an answer, store it and never recompute it again.
The other problem is that the input may contain cycles. In that case our code would fail as well (either with a timeout, or with an incorrect answer, depending on exactly when we change the memoized value). To handle cycles correctly, we have to be able to detect them. Once we detect a cycle, we can immediately return -1.
Plenty of failed solutions show that detecting cycles is not as easy as it might seem. For example, many solutions fail on the following case:
3HH5HHHHHH HHHHHHHHHH HHHHHHHHHH 5HH4H2H8HH HHHHHHHHHH HHH2HHHHHH
The reason why the solutions failed is that there are two different ways how to reach the cell with the number 4 -- and the failed solutions just noted "I already discovered this cell" and incorrectly assumed that they found a cycle.
The correct reasoning is a bit different: we found a cycle if and only if we are making a move from a cell C to some other cell we used on the way to C. How to implement this check? When you enter a cell for the first time, set its state to "being processed". Once you try to enter such a cell for the second time, you just discovered a cycle. When you finished processing the cell (and everything that is reachable from the cell), change its state from "being processed" to "done", and store the answer for this cell.
(Again, a sketch of a proof why this works: If there are no reachable cycles, the situation above clearly can't happen. If there are reachable cycles, sooner or later it will happen that we visit the last cell of one of the cycles. At this moment, all of the cycle's cells are marked as "being processed", and when processing the children of the current cell you will discover this cycle.)
The code with both fixes (memoization and cycle detection) follows:
int[][] memo;
int getResult(int r, int c) {
if (r<0 || r>=R || c<0 || c>=C) return 0;
if (memo[r][c] >= 0) return memo[r][c];
if (memo[r][c]==-2) return 987654321; // we found a cycle, return infinity
memo[r][c]=-2; // set the cell to "being processed"
int res = 0;
int jumpLength=B[r].charAt(c)-48;
for (int d=0; d<4; d++)
res = Math.max(res, 1+getResult( r+jumpLength*dr[d], c+jumpLength*dc[d] ) );
memo[r][c] = res;
return res;
}
int solveRecursively() {
memo = new int[R][C];
for (int r=0; r<R; r++) for (int c=0; c<C; c++)
if (B[r].charAt(c)=='H') memo[r][c]=0; else memo[r][c]=-1;
int x = getResult(0,0);
if (x > 900000000) return -1;
return x;
}
The time complexity of this solution is O(RC).
Exercises
- 3.1 How would the problem change if you were allowed to pick the starting cell? Is it still possible to solve it in O(RC)?
- 3.2 How large can the answer be? The largest test case I used in the systests had the answer 1057, but there is clearly plenty of space for improvement.
- 3.3 Explain how is depth-first search on a directed graph related to our second solution.


Used as: Division One - Level Two:
Value 500 Submission Rate 254 / 523 (48.57%) Success Rate 80 / 254 (31.50%) High Score bmerry for 442.58 points (10 mins 30 secs) Average Score 277.29 (for 80 correct submissions)
A high-level idea of the solution should be pretty clear: For each pair of polylines, find out whether they intersect. Build a graph where the vertices correspond to polylines, and edges mean that the polylines have a point in common. The answer is the number of components of this graph.
We'll start with the last part. The input can contain at most 625 polylines (each consisting of a single point). This means that the O(N3) Floyd-Warshall algorithm will be pretty close to the time limit. As a contestant in C++ I would go for Floyd-Warshall without hesitation, but for the reference solution I implemented an O(N2) breadth-first search instead:
int countComponents(boolean[][] G) {
int N = G.length;
boolean[] used = new boolean[N]; for (int i=0; i<N; i++) used[i]=false;
int[] Q = new int[N+10];
int qs=0, qf=0;
int res = 0;
for (int i=0; i<N; i++) if (!used[i]) {
res++;
qs=0; qf=1; Q[0]=i; used[i]=true;
while (qs<qf) {
int k = Q[qs++];
for (int j=0; j<N; j++) if (G[k][j]) if (!used[j]) {
Q[qf++]=j;
used[j]=true;
}
}
}
return res;
}
How to check whether two polylines intersect? This can again be broken down to a simpler problem: check whether two (possibly degenerate) line segments intersect. To check whether two polylines intersect, simply iterate over each polyline's segments:
boolean polylinesIntersect(int x, int y) {
for (int i=0; i<len[x]; i++) for (int j=0; j<len[y]; j++) {
int ii=i+1, jj=j+1;
if (ii==len[x]) ii--; if (jj==len[y]) jj--;
if (segmentsIntersect(x,i,ii,y,j,jj)) return true;
}
return false;
}
Note that our code transparently handles polylines consisting of a single point by duplicating the last point of each polyline.
Checking whether two line segments AB and CD intersect is a pretty standard task. One possible way is to start by checking whether one of the endpoints lies on the other segment. If this is true, return true. Otherwise the segments can only intersect in an inner point. This happens if and only if (A and B lie on different sides of CD, and C and D lie on different sides of AB). Using vector operations both checks can be implemented in such a way that they work for degenerate cases as well.
Exercises
- 4.1 Show how to answer the question "do points A and B lie strictly on different sides of the line CD" using vector products only. Your method should return false if C=D.
- 4.2 Show how to answer the question "does point A lie on the segment BC" using vector and scalar products only.
- 4.3 What is the maximum number of intersections one can get for a valid input?


Used as: Division One - Level Three:
Value 1000 Submission Rate 18 / 523 (3.44%) Success Rate 1 / 18 (5.56%) High Score cnettel for 557.23 points (31 mins 7 secs) Average Score 557.23 (for 1 correct submission)
This problem can be approached in several ways. In this editorial we will describe the idea that was implemented as the reference solution, and the thought process used to design it. It is not the simplest solution possible, but it contains a lot of insight into the problem, and a theoretical upper bound that guarantees it to pass system tests.
First of all, we'll explain one issue that's not really related to the actual problem: there is no difference between an ambiguous and a really ambiguous code. This is because if a code is ambiguous, there is a string S that has at least two decodings. But then the string SS (two copies of S, one after another) has at least four decodings, and thus the code is really ambiguous. Of course, the shortest counterexample does not have to be of this form.
We will explain the ideas behind our solution both theoretically, and on the following example code:
{"110010","10","1100","110","0101010","001","001110","001001110"}
This code is (really) ambiguous. One possible proof is that
the string 1100101010 has these three decodings:
1100101010 = 110010 + 10 + 10
= 1100 + 10 + 10 + 10
= 110 + 0101010
In the rest of the text, the term code words will mean
the elements of the input array code.
We will use the term string to denote a concatenation
of some code words.
In our solution we will try to assemble some string from
the given code words in three different ways.
Basic observations
Warning. This section deliberately ignores one issue. Don't worry, everything will be handled in detail later.
Given a code, how can we find a proof that it is really ambiguous?
We have to create some string in three different ways.
We can start by picking three
code words we will start with. In the example above, these would be
110010 for the first way, 1100 for the second
and 110 for the third way.
Note that we can not just choose any three code words. It only makes sense to choose code words such that all of them are prefixes of the longest one we choose -- otherwise the constructed strings can not be equal.
Now, imagine a graph where the vertices have the form
(string1, string2, string3).
For example, the situation after picking the initial code words
in the example above would correspond to the vertex
(110010,1100,110).
The edges in this graph will be directed, and they will correspond
to adding a code word to one of the three strings.
In our example, adding the code word 10
to the first string would take us to the vertex
(11001010,1100,110).
Clearly, the code is ambiguous if and only if we can reach a vertex with three equal strings. This brings us to the idea of our first attempt at a solution.
First attempt at a solution
One thing our graph is still missing is a way how to find the shortest counterexample. But this can easily be solved: our solution will process the vertices ordered by the length of the longest of the three strings. If we do it this way, once we find a vertex with three equal strings, we can be sure that no other vertex will correspond to a better solution.
A different way of looking at the algorithm:
we will add edge lengths. The length of an edge will
represent the increase in the length of the longest
string. For example, the edge from
(110010,1100,110) to
(11001010,1100,110) will have length 2,
the edge from (110010,1100,110) to
(110010,110010,110) will have length 0.
In this graph the answer to our original question
is simply the length of the shortest path to a
vertex of the form (S,S,S).
And our algorithm is suddenly nothing else but a
plain Dijkstra's shortest path algorithm.
Still, we have a long way to go. For example, our graph has infinitely many states, and we still can not tell when to stop looking and decide that the code is not ambiguous.
Smaller states
Note that it makes no sense to store three strings in the state, as two of them are always prefixes of the third one. We can simply store the longest string, and the number of letters missing in the second and the third string.
For example, the state (110010,1100,110)
will change to (110010,2,3).
"Less" states
Now the insight with Dijkstra's algorithm will start to matter. We will now merge some states together. We are trying to answer questions of the form: "What is the shortest way of extending these three strings to get the same final string?". The important observation is that the answer to such a question does not depend on the part that all three strings have in common.
For example, if it is possible to reach a final vertex from (110010,1100,110),
then it is also possible to reach a final vertex
from (010,0,) -- by adding the same code words.
Of course, the graph would still remain infinite. For now, just keep this optimization in mind, we will use it later, when it will make more sense.
Getting a finite graph
The next thing we should notice is that making
a move like (110010,1100,110) to
(11001010,1100,110) is pretty much
pointless. If we are in a "wrong" vertex that does
not lead to a solution, we can discover it earlier
by trying (and failing) to extend the shorter strings.
If we are in a "right" vertex, we can still gain
something by only trying to extend the shorter strings
-- we'll only try the possibilities that make sense
at the moment.
So much for intuition, and now a formal conclusion. From now on, in our solution we will only try to extend the shortest of the three strings.
Clearly, we lost nothing -- every final vertex that was reachable before will still be reachable (only the number of ways how to reach it decreased).
On the other hand, did we gain something? We will show that we did. If we use our new approach, the three strings will always have similar lengths. But this means that our optimization from the previous section could really help. We will now prove this.
Theorem: Suppose that we use the strategy that always extends the shortest string. Then the difference between the longest and the shortest string is always a suffix of some code word.
Proof: After picking the initial code words this is clearly true. Now suppose that we are in a vertex where it is true, and we extend the shortest string using some code word C. There are two possibilities: Either the extended string is now the longest one, or not. Refer to the ASCII art below. In the first case, the difference is now a suffix of C, in the second case, it is still the suffix of the same code word as before.
Case 1:
|----string-1--|-last-word-|
|----string-2------|
|----string-3----|-----C--------|
|-difference-|
Case 2:
|----string-1--|-last-word-|
|----string-2------|
|----string-3----|--C--|
|-diff.-|
The conclusion: each state of our search can be represented by three small integers: the index of the code word at the end of the longest string, and two offsets stating how many letters are missing in the second and the third string.
A longer example
We will now show the entire path that corresponds to our well known example. For reference, we now repeat the code words, this time with their indices.
{#0: "110010", #1:"10", #2: "1100", #3: "110",
#4: "0101010", #5: "001", #6: "001110", #7: "001001110"}
Path in the original graph:
start -> (110010,1100,110) -> (110010,1100,1100101010) -> (110010,110010,1100101010) -> (four more steps where we add 10) (1100101010,1100101010,1100101010)
Path in the compressed graph:
start -> [edge cost 6] (#0,2,3) -> [edge cost 4] (#7,4,6) -> [edge cost 0] (#7,4,4) -> (four more steps where we add 10) (#7,0,0)
Fixing what we ignored so far
The observations made so far would be sufficient to implement a solution... except that we ignored an important detail. The detail is that in the optimal solution two of the three strings may start with the same code word. In our example code, notice the following solution:
001001110 = 001 + 001 + 110
= 001 + 001110
= 001001110
The problem is that if we are in the state where two strings
are equal (e.g. (001001110,001,001)),
we have to know whether the two equal strings were constructed
in the same way or not.
Summary: a complete solution
Suppose that there are W code words, each with at most N characters. We will build a graph with 3WN2 vertices. Each vertex is an ordered quadruple (code word index, offset1, offset2, situation type). There can be three situation types:
- type 0: all three strings are constructed in different ways
- type 1: the two longer or equal strings are constructed in the same way
- type 2: the two strictly shorter strings are constructed in the same way
In the beginning, brute force over all pairs and triplets of initial code words and fill the priority queue. From now on, repeat: pop a vertex from the queue, try all ways how to extend the shortest code word, whenever you improve the shortest path to some vertex, insert it into the priority queue. Once you pop a final vertex (one where both offsets and situation type are zero), return its distance. Once the queue is empty, you know that the code is not ambiguous, and you can return -1.
Note that in situation 2 we have two ways how to extend: Either extend both strings using the same code word (and remain in situation 2 or 1), or use two different code words to get to situation 0.
Exercises
- 5.1 Derive close asymptotic bounds for the number of edges in our graph and for the time complexity of our algorithm.
- 5.2 Given a non-ambiguous binary code, how efficiently can you decode strings of zeros and ones? How does the situation improve if the code is a prefix code?
