
|
Match Editorial |
Wednesday, September 26, 2007
Match summary
In both divisions coders were faced by a quite balanced problem set. Almost all of the problems provided pretty good challenge opportunities.
In Division 1 gozman took the lead after the coding phase and stayed on the top until the system testing. But his success rate (especially on the problems of the hard category) confirmed its relevance, and he fell from the much-desired first place. Only 13 solutions of the hard problem passed the system tests, thus fortune rewarded good challengers and fast coders. ACRush won the match, gawry finished second, and third place went to Per.
Spectators saw plenty of failed solutions in Division 2 as well. The number of failed solutions of the medium and hard problem was quite large; in some rooms, it was even possible to take the lead without a correct solution of the hard problem, as long as you had plenty of challenges. espr1t took first place without any challenges at all, thanks to a pretty high score on all of the problems. cytmike finished second with 3 successful challenges, with newcomer snguyen in third.
The Problems
WhiteCells

Used as: Division Two - Level One:
Value 250 Submission Rate 681 / 706 (96.46%) Success Rate 672 / 681 (98.68%) High Score catcher for 249.42 points (1 mins 22 secs) Average Score 226.13 (for 672 correct submissions)
All the rows of a chessboard divide into two categories: even and odd.
Within an even row, all cells located in even columns are white, while all
that are in odd columns are black. Within an odd row, all white cells are
located in odd columns, while blacks are in an even columns.
Thus, the cell is black if and only if its row and column numbers have the same parity.
So, it is possible to iterate over all cells and count the number
of occupied whites. An alternative approach is to iterate only over
white cells. This idea is implemented in the C++ listing below:
struct WhiteCells {
int countOccupied(vector <string> board) {
int ret = 0;
for (int i = 0; i < board.size(); i++)
// j must have the same parity as i
for (int j = i % 2; j < board[i].size(); j += 2)
if (board[i][j] == 'F') ret++;
return ret;
}
};
ObtainingDigitK


Used as: Division Two - Level Two:
Used as: Division One - Level One:
Value 500 Submission Rate 630 / 706 (89.24%) Success Rate 233 / 630 (36.98%) High Score winterflame for 493.78 points (3 mins 11 secs) Average Score 362.17 (for 233 correct submissions)
Value 250 Submission Rate 589 / 597 (98.66%) Success Rate 419 / 589 (71.14%) High Score cep21 for 249.21 points (1 mins 36 secs) Average Score 220.39 (for 419 correct submissions)
This task asked coders to find the minimal possible number x that could be added to the given number a in such a way that their sum (a + x) contains at least one instance of a given digit k.
Approach 1 - Brute-force
Let's brute-force x starting from 0 and check if (a + x) contains digit k.
This idea looks very simple, but don't forget that a may not fit in 64-bit integer.
Java users are strongly aided by BigInteger class, but it is not much trouble for others
to implement a function that increments a long number by one (actually it's enough, because when
we increment x, we can use the already calculated (a + x - 1) to obtain (a + x)).
Approach 2 - Examining cases
Let d be the least significant digit of a and d' be the least significant digit of a + x.
It's obvious that x can't be more than 9, because we make d'
to have any value (from 0 to 9, inclusive) using x ≤ 9.
The first thing to do is to check if a already contains a digit k,
in this case the answer is 0.
Then, if d is less than or equal to k, then x = k - d.
Otherwise, we need to find the digit to the left from d, skipping all the nines. Let's call this digit z.
For example, if a = 12399997, then d = 7 and z = 3.
If a = 997, we can treat it as 0997, thus z = 0 in this case.
Now, let's examine z: if it is equal to k + 1, then x = 10 - d, because
using this x, the digit in position of digit z increments by one and becomes equal to the desired value k.
In the other case the answer is 10 + k - d (raising d to k).
As you can see, this approach requires much more thinking the the previous one.
Moreover, if the coder will not notice at least one of the mentioned cases, his solution will most probably fail.
Most Division 1 coders used the first approach, thus avoiding a lot of pitfalls. Many Division 2 coders, however, ran into problems by using the second approach.
ProgrammingDevice

Used as: Division Two - Level Three:
Value 1000 Submission Rate 286 / 706 (40.51%) Success Rate 48 / 286 (16.78%) High Score espr1t for 841.98 points (12 mins 48 secs) Average Score 527.09 (for 48 correct submissions)
The first thing to do here is to realize that we must send full packets only, because (in contrast to div 1 medium)
we need to minimize the number of packets, but not anything else. Also, we need to realize that there is no reason to
send any unimportant bytes (which don't belong to any of the given pieces) in the beginning of the packet, i.e. each
packet must begin with an important byte.
The second is to sort all the given pieces in ascending order of their offsets.
Once the mentoined sorting is done, we can easily iterate over pieces in the "from left to right" order
and greedily send as much data by one packet as possible. In order to fit under the 2 second running time
we need to use the following trick: determine the number of packets necessary to entirely cover the current piece,
and treat them all at once (which leads to O(n ^ 2) complexity, where n is the number of pieces) .
The desired number can be obtained by dividing the amount of unsent bytes of the current piece
by the maximal allowed size of the packet, rounding the result to the up.
C++ code follow:
struct ProgrammingDevice
{
int minPackets(vector <int> offset, vector <int> size, int maxData) {
// pos - position of the first (leftmost) non-sent important byte
long long pos, k;
int ret = 0, n, i, j;
n = offset.size();
// sort pieces
for (i = 0; i < n; i++) for (j = i + 1; j < n; j++)
if (offset[i] > offset[j]) {
swap(offset[i], offset[j]);
swap(size[i], size[j]);
}
i = 0; // begin from the leftmost piece
// set the pos equal to the first important byte
pos = offset[0];
// process until all important bytes are sent
while (pos < offset[n - 1] + size[n - 1]) {
// k - the number of packet neccessary tosend in order
// to cover whole the current piece i
k = (offset[i] + size[i] - pos + maxData - 1) / maxData;
ret += k;
// always send a full packets
pos += maxData * k;
// find the leftmost piece which is not entirely sent yet
for (; i < n; i++) if (pos < offset[i] + size[i]) break;
// skip all contiguous unimportant bytes located to the left of the piece i
if (i < n && pos < offset[i]) pos = offset[i];
}
return ret;
}
};
DeviceProgramming


Used as: Division One - Level Two:
Value 500 Submission Rate 313 / 597 (52.43%) Success Rate 190 / 313 (60.70%) High Score bmerry for 480.61 points (5 mins 45 secs) Average Score 290.50 (for 190 correct submissions)
Both approaches to solving this one are based on the idea of dynamic programming and assume that pieces are previously sorted in ascending order of their offsets. The following symbols are used:
- n - the number of pieces
- m - the maximal number of contiguous bytes that can be sent in one packet, i.e. m = maxPacket - overhead
- dp - the array, which contains the answers for DP subproblems
Approach 1
The DP state is (i, j), where i is the index of the current piece and j is the position in this piece
(all bytes to the left of this position are already sent, while all the others did not).
The starting state is (0, 0). dp[i][j] contains the amount of bytes neccessary to send all important bytes
(a byte is important if it belongs to some of the pieces) located to the right of the j-th byte of the i-th piece and this byte itself too.
Let's determine what is the maximal number of full packets, containing the bytes
starting from the j-th byte of the current piece only, we can send. It is equal to (size[i] - j) / maxData (rounding down).
Once we have sent these packets, the j has been changed.
Now, there are O(n) possible moves. We must try to move to all states (k, 0), where i < k < n,
which are reachable from the current state within one packet. Actually the state (k, 0) is reachable from the state
(i, j) if offset[i] + j + m >= offset[k - 1] + size[k - 1].
Thus, complexity of the described algorithm is O(n * m * n).
Approach 2
The state is i, where i is the index of the current piece.
dp[i] contains the answer for the subproblem, considering only i leftmost pieces.
As an initial value of dp[i] for each 0 ≤ i < n
we try to send all bytes from the leftmost byte of the piece 0 to the last byte of the i-th piece,
inclusive (greedily packing these bytes into packets), possible including unimportant bytes which may lie between them.
There are O(n) possible moves from state i: to states j, where 0 <= j < i.
A move is always possible each time we send all the bytes from the leftmost byte of the i-th piece
to the rightmost byte of the j-th piece, inclusive (greedily packing bytes into packets), and add dp[j].
Java code of the very elegant solution by ivan_metelsky illustrates the second approach:
public class DeviceProgramming {
public long getSize(long maxPacketSize, long overhead, long size) {
long maxInfo = maxPacketSize - overhead;
long packetsNeeded = (size % maxInfo == 0 ? size / maxInfo : size / maxInfo + 1);
return size + packetsNeeded * overhead;
}
public long minBytes(int[] offset, int[] size, int maxPacketSize, int overhead) {
int N = offset.length;
int[] st = new int[N], fn = new int[N];
for (int i=0; i < N; i++) {
st[i] = offset[i]; // beginning of the piece
fn[i] = offset[i] + size[i] - 1; // end of the piece
}
// sort the pieces
for (int i=0; i+1 < N; i++)
for (int j=0; j+1 < N; j++)
if (st[j] > st[j+1]) {
int tmp = st[j]; st[j] = st[j+1]; st[j+1] = tmp;
tmp = fn[j]; fn[j] = fn[j+1]; fn[j+1] = tmp;
}
long[] F = new long[N];
for (int i=0; i < N; i++) {
// calculate the initial answer
F[i] = getSize(maxPacketSize, overhead, fn[i] - st[0] + 1);
for (int j=1; j <= i; j++)
// try to move to state j
F[i] = Math.min(F[i], F[j-1] + getSize(maxPacketSize, overhead, fn[i] - st[j] + 1));
}
return F[N-1];
}
}
WSNParentsAssignment


Used as: Division One - Level Three:
Value 1000 Submission Rate 60 / 597 (10.05%) Success Rate 13 / 60 (21.67%) High Score ACRush for 695.05 points (20 mins 50 secs) Average Score 500.04 (for 13 correct submissions)
This is a max flow problem. There is a wireless sensor network (WSN) graph shown in figure 1 and its corresponding flow-graph in figure 2.
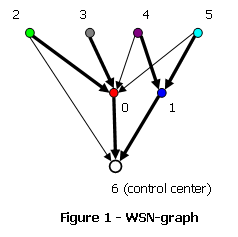

Vertices of the WSN-graph are devices and a control center of the WSN. Edge from vertex i to vertex j exists if and only if the device corresponding to vertex i can transmit data directly to the device corresponding to vertex j. Edge from the vertex i to the vertex, corresponding to the control center, exists if and only if the device corresponding to vertex i can trasmit directly to the control center. Building a flow-graph is a much more sophisticated task. It requires accomplishing the following steps (assuming that the flow-graph is initially empty):
- Add source and sink vertices;
- For each device add two vertices: "left half" and "right half";
- For each device add an edge from its "right half" to the sink of capacity 1;
- For each device, which can transmit directly to the control center, add an edge from source to its "right half" of capacity 1;
- For each pair of devices i and j, if device i can transmit directly to device j, add an edge from the "left half" of device j to the "right half" of device i of capacity 1;
- For each device add an edge from source to its "left half" of capacity k.
Once the minimal network's burden level is found, the parents vector should be built. This task can be solved by greedy algorithm combined with a brute-force. Iterate over the device in ascending order of their indices and find the minimal possible index of its parent, which leads to the minimal network's burden level equal to the previously found minima, using a brute-force. Once it is declared that device j is the parent of device i, edge from the "right half" of device i should be removed and the capacity of the edge from the "left half" of device j to the "right half" of device i should be decreased by 1.
