
|
Match Editorial |
Thursday, January 4, 2007
Match summary
If someone asked me to characterize the problem sets (for both divisions) in one sentence, I would say "pay attention to details, it will pay off twice." This time my goal was to make a problem set that would lead to an interesting challenge phase. And so it was --but let's start at the beginning.Most Division 1 coders started the day by opening the easy problem – a string parsing problem where the most difficult part was to check whether a part of the string represents a valid date. When it comes to dates and times, it's good to be careful, and so it took a while until we saw the first submission. (Its author was no surprise at all. Try to guess and verify it below.) In the next few minutes, we saw a plenty of submissions on the easy problem and then... nothing.
Almost half an hour into the coding phase HardCoder was the first to submit the hard problem, with no submissions on the medium yet. His solution didn't even pass some of the examples, but it was apparently enough to get the top competitors thinking "umm, did I miss some easy way how to solve it?" (A notable fact is that HardCoder's 1000 survived for a surprisingly long part of the challenge phase. Was nobody willing to take the risk and challenge it?)
Three minutes later we saw the first submissions of the medium problem. In a matter of seconds, four coders submitted their solutions. It's almost unbelievable how balanced the top coders are.
At 52 minutes into the competition andrewzta submitted his solution for the hard problem and took the lead, being the first person to complete the set... or not? Sadly for him, testing revealed a hidden bug in his 1000, and eight minutes later he had to resubmit.
Submissions continued to pour in. When the coding phase ended, the coders could take a look at the division summary, only to discover that none of the competing targets had submitted the hard problem -- in fact, the best performance among the targets was Petr's, who was in 22nd place.
But that was all about to change when the challenge phase started. Day equal to zero? A string of zeroes ending just outside of T? The volume of a 1×1×1 pyramid? The possibilities to gain points were almost endless, and many coders used them to move up the ranklist. For example, jakubr's six successful challenges (and one wrong) brought him to 6th place overall. Other good challengers were Vytenis (7 good, 1 bad, 11th overall) and zmaks (5 good, 17th overall).
During the challenge phase the leader changed almost every minute. We saw andrewzta leading the pack, then HiltonLange, not2knight, ... and in the last minutes of the challenge phase Per claimed the top spot for a while. But the challenge wasn't over yet.
After the system tests we saw that only two coders had solved all three tasks: the SRM winner and new target Egor, and fellow Russian andrewzta. Speaking of fellow Russians, just look at the next three places: not2knight, Petr and falagar are all from Russia, too. Quite a day for them!
The Division 2 match was pretty similar to what was happening in Divion 1. The coders started off with a pretty easy 250, then solved the same two problems as the Div1 easy and medium. The Div1 medium / Div2 hard problem proved to be too tricky for this division – due to the time pressure, none of the 62 submissions was flawless.
Newcomer ilyaraz was the first to submit both the easy and the medium problem. But with a tricky medium and hard, even this was not enough to win the division. Several more experienced coders were much more successful in challenging, and the challenge phase was what determined the top spots in the division.
A notable event were EmperorofUnivrs's challenges (9 good ones and a bad one) which gave him 12th place overall with only the easy problem solved.
The top three places were claimed by AJA, hutelang and arviman. Each of them had to make at least 4 successful challenges to get to the top.
The Problems
ChessboardPattern

Used as: Division Two - Level One:
An easy problem to get everyone started. It can easily be seen that the constraints in the problem statement really define a chessboard-like pattern.
Value 250 Submission Rate 532 / 580 (91.72%) Success Rate 498 / 532 (93.61%) High Score MMLEI for 249.26 points (1 mins 33 secs) Average Score 203.98 (for 498 correct submissions)
Consider the squares (0,0) and (i,j). If (i+j) is even the squares have the same symbol, if (i+j) is odd they have different symbols. Thus the symbol at coordinates (i,j) depends only on the value (i+j) modulo 2.
In addition, we know that the symbol at (rows-1,0) is a dot. This gives us enough information to fill the whole chessboard at once.
Java code follows:
public String[] makeChessboard(int rows, int columns) {
String[] result = new String[rows];
for (int i=0; i<rows; i++) result[i] = "";
for (int i=0; i<rows; i++)
for (int j=0; j<columns; j++)
if ( ((rows-i+j) % 2) == 0)
result[i] += "X";
else
result[i] += ".";
return result;
}
BirthNumbersValidator


Used as: Division Two - Level Two:
Used as: Division One - Level One:
Value 500 Submission Rate 437 / 580 (75.34%) Success Rate 147 / 437 (33.64%) High Score ilyaraz for 450.53 points (9 mins 37 secs) Average Score 289.83 (for 147 correct submissions)
This was an example of a real life problem. We can split the checking into several logical steps. And if we can do this, it's almost always a good idea to actually do it. The resulting code will be much less error prone.
Value 250 Submission Rate 434 / 439 (98.86%) Success Rate 281 / 434 (64.75%) High Score antimatter for 241.73 points (5 mins 17 secs) Average Score 194.16 (for 281 correct submissions)
The things we need to check:
- Is the number divisible by 11?
- Does it contain a valid date?
For the validity of a date we will start by introducing some helper functions: The function
isLeap(year) will compute whether the year is a leap year,
and the function getDaysInMonth(month,year) will return the number of days
in the given month. Note that we need to give the year as the second argument to handle
leap years properly.
boolean isLeap(int y) { return (y%4 == 0); }
int[] daysInMonth = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
int getDaysInMonth(int m, int y) { if (m==2 && isLeap(y)) return 29; return daysInMonth[m-1]; }
Now we are ready to process the string:
public String[] validate (String[] test) {
int N = test.length;
String[] result = new String[N];
for (int i=0; i<N; i++) {
result[i] = "NO";
// check for divisibility
long value = Long.parseLong(test[i]);
if (value % 11 != 0) continue; // the answer remains NO
// parse the stored date
int year = Integer.parseInt( test[i].substring(0,2) );
int month = Integer.parseInt( test[i].substring(2,4) );
int day = Integer.parseInt( test[i].substring(4,6) );
// adjust the parsed values
year += 1900; if (year <= 1906) year += 100;
if (month >= 50) month -= 50;
// check whether the date is valid
if (month < 1 || month > 12) continue;
if (day < 1 || day > getDaysInMonth(month,year)) continue;
result[i] = "YES";
}
return result;
}
By far the most common error was forgetting that neither day 00 nor month 00 (or 50) is a valid input.
RepeatedPatterns


Used as: Division Two - Level Three:
Used as: Division One - Level Two:
Value 1000 Submission Rate 62 / 580 (10.69%) Success Rate 0 / 62 (0.00%) High Score null for null points (NONE) Average Score No correct submissions
This was one tough ad-hoc problem. The problem statement is short and simple, for the whole time it is clear what to do, and almost clear how to do it. Still, to more experienced coders the problem statement seems to scream "mind the details"! Slowing down and making sure you didn't miss anything is a good investment whenever you encounter a similar problem.
Value 500 Submission Rate 205 / 439 (46.70%) Success Rate 21 / 205 (10.24%) High Score andrewzta for 346.63 points (20 mins 57 secs) Average Score 237.91 (for 21 correct submissions)
So, let's approach the problem slowly. We will split the solution into four cases, depending on whether the patterns P1 and P2 contain at least one '1'.
The simplest case is when both P1 and P2 contain only '0's. In this case for any zeroCount the answer is simply 0.
boolean P1zero = P1.matches("0*");
boolean P2zero = P2.matches("0*");
if (P1zero && P2zero) return 0; // the sequence occurs at index 0
Another simple case is when both P1 and P2 contain some '1's. In this case the longest
sequence of '0's will be pretty short. Clearly, it can not contain an entire pattern.
Thus, if there is a sequence of zeroCount '0's, it has to be a subsequence of P1+P1,
of P1+P2, of P2+P1, or of P2+P2. We find the earliest match (if any) and output it:
int checkString(String haystack, long zeroCount) {
if (zeroCount > haystack.length()) return -1;
String needle=""; for (int i=0; i<zeroCount; i++) needle += "0";
return haystack.indexOf(needle);
}
// ...
if ((!P1zero) && (!P2zero)) {
int x;
x = checkString(P1+P1,zeroCount); if (x>=0) return x;
x = checkString(P1+P2,zeroCount); if (x>=0) return x + 999999*P1.length();
x = checkString(P2+P1,zeroCount); if (x>=0) return x + 1000000*P1.length();
x = checkString(P2+P2,zeroCount); if (x>=0) return x + 2000000*P1.length() + P2.length();
return -1;
}
If P1 contains only '0's and P2 contains some '1's, there are three cases:
- If there are at least zeroCount '0's at the beginning, the answer is 0.
- Else, there may be a longer string of '0's that starts within the first occurence of P2, contains 1,000,000 occurences of P1 and the beginning of the second P2.
- If zeroCount exceeds the length of that substring, the answer is -1.
// compute the information on the number of head/tail zeroes
String zeroes="";
int P1head=0, P1tail=0, P2head=0, P2tail=0;
for (int i=1; i<=50; i++) {
zeroes += "0";
if (P1.startsWith(zeroes)) P1head = i; if (P1.endsWith(zeroes)) P1tail = i;
if (P2.startsWith(zeroes)) P2head = i; if (P2.endsWith(zeroes)) P2tail = i;
}
if (P1zero && (!P2zero)) {
// types of segments:
// - at the beginning
// - between two P2s
int beginning = 1000000 * P1.length() + P2head;
int between = P2tail + 1000000 * P1.length() + P2head;
if (beginning >= zeroCount) return 0;
if (between >= zeroCount) return 1000000 * P1.length() + P2.length() - P2tail - 1;
return -1;
}
The last remaining case is when P2 has only '0's and P1 has some '1's. In this case
S will contain an arbitrarily long zero substring, the trick is to find whether it occurs soon
enough... and for small zeroCount you also shouldn't miss the chance of seeing the
substring before you even get to the first P2.
Thus, first we check whether P1+P1 contains a long enough substring. If not, the first occurrence will be a substring of "tail zeroes in P1 + several times P2 + leading zeroes in P1". We can easily compute the smallest number of P2s we need. Now all is left is to check whether this substring occurs early enough in S. To avoid overflow, in my solution I used binary search to find the largest N such that T contains a part of S(N).
long TEN_TO_SIXTEEN = 1; for (int i=0; i<16; i++) TEN_TO_SIXTEEN *= 10;
if ((!P1zero) && P2zero) {
// types of segments:
// - inside P1 + P1
// - between two P1s with sufficiently many P2s
int x = checkString(P1+P1,zeroCount); if (x>=0) return x;
zeroCount -= P1tail;
zeroCount -= P1head;
long lo=0, hi=1;
while (getLength(P1.length(), P2.length(), hi) < TEN_TO_SIXTEEN) hi *= 2;
while (hi-lo > 1) {
long med = (lo+hi)/2;
if (getLength(P1.length(), P2.length(), med) < TEN_TO_SIXTEEN) lo=med; else hi=med;
}
long mostP2s = hi;
long needsP2s = (zeroCount + P2.length() - 1) / P2.length();
if (mostP2s < needsP2s) return -1;
long index = needsP2s * 1000000 * P1.length() + (needsP2s * (needsP2s-1)) * P2.length() / 2 - P1tail - 1;
if (index + zeroCount > TEN_TO_SIXTEEN) return -1;
return index;
}
Note that much shorter solutions are possible. E.g., in the solution presented above, many cases could
be merged together – but the price to pay makes it not worth the trouble in a real contest.
However, IMHO this problem is a great candidate for a shortest code contest... why don't you give it
a try? :-)
ThreeBuses


Used as: Division One - Level Three:
In this task we have to deal with probability in a setting when there is an infinite number of possible outcomes. In many such situations, geometry may help.
Value 1000 Submission Rate 20 / 439 (4.56%) Success Rate 5 / 20 (25.00%) High Score not2knight for 601.81 points (20 mins 26 secs) Average Score 518.22 (for 5 correct submissions)
Before you start reading, scroll down to see the long and ugly code necessary to solve the general case. After you are properly amazed, scroll back here and start reading the solution
:-)
Introduction
Let's start with a simple example. Suppose I have a stick 1 meter long. I break it in a random place. What is the probability that both parts will be at least 40 cm long?We may draw a picture representing the stick:
0 50 100 |---|---|---|---|---|---|---|---|---|---| | A | B | C |If the breaking point falls into A or C, one of the sticks will be too short. On the other hand, if the breaking point falls inside B, both sticks will be long enough. Thus the probability is (length of B) / (length of the stick) = 20 / 100 = 20%.
Simplifying the problem
Clearly, Johnny has to spend (travel[0] + travel[1] + travel[2]) minutes traveling. We may subtract these from timeLeft and forget about them from now on.If all values in wait[] are zero, the outcome is clear and we output it immediately.
One bus
If Johnny had to ride only one bus, we get a very similar problem. The stick will represent the interval [0,W], and the good part of the stick will be the interval [0,min(timeLeft,W)].Note that we get this case when two of the values in wait[] are zero.
Two buses
Now it starts to become interesting. The possible outcomes can no longer be mapped to a stick. Instead, we have to use two dimensions. Let WX and WY be the maximum wait times for the two buses. All possible outcomes of Johnny's trip correspond to points inside an axes-parallel rectangle with corners in [0,0] and [WX,WY]. Good outcomes will correspond to those points [x,y] where x+y≤timeLeft.Let's take a closer look at how the set of good outcomes looks like.
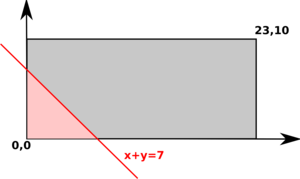
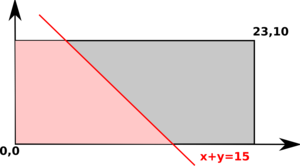

The lines "x+y = constant" are parallel and have a 45 degree angle with the x axis. The good outcomes are those on this line and in the halfplane to the left of it. In the pictures the good outcomes are in pink.
The answer in this case, of course, is (pink area) / (rectangle area). In cases corresponding to the images 1 and 3 we just need to compute the area of a right triangle, in the second case a right trapezoid. Elementary school math is enough here. You may note that the second case only occurs whenever one of the rectangle's dimensions exceeds twice the other.
double area(int x, int y, double sum) {
if (sum <= 0) return 0.0;
if (x>y) { int z; z=x; x=y; y=z; }
double result = x*y;
if (sum <= x) result = 0.5*sum*sum; else
if (sum <= y) result = 0.5*(2*sum-x)*x; else
if (sum <= x+y) result = x*y - 0.5*(x+y-sum)*(x+y-sum);
return result;
}
Three buses
The concept for the next step should be clear. All outcomes = a WX × WY × WZ box. Good outcomes: everything on or below the plane x+y+z = timeLeft.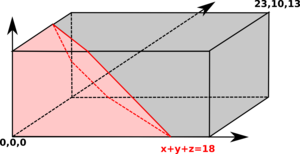
The problem is that computing the volume can be quite ugly, and the number of different cases is much larger than before. Sure, there is an O(1) solution, but let's think how can we make our life easier.
One possible trick: Consider an arbitrary horizontal cut through our box. Suppose that Y is the height of the cut. What we get is a 2D version of our problem with x+z <= timeLeft-Y.
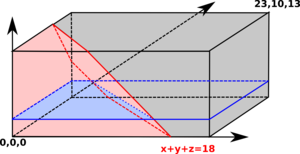
(Now there's a way how to write a reasonable O(1) solution using high-school math only: Find all vertices of the "good outcomes" polyhedron, put a horizontal cut through each of them, and find a formula for the volume of each of the pieces you'll get. In the rest of this solution we will show how to use calculus to obtain a solution that is way easier to implement.)
Using the
area() function as defined above, we can express the area of the cut as
area(WX,XZ,timeLeft-Y).
Now, the volume of the good part can be written as
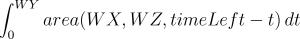
Imagine that we start with the cut at Y=0, and now start to increase Y. How will the area of the cut change? For a while it may be constant, then it will decrease, until it's zero or we get to Y=WY.
Remember that there were 3 types of areas when handling the 2D situation. (Umm, more precisely, there were 5 cases. The area can also be equal to the entire rectangle, or it can be zero. To see an example when this happens, consider WX=WZ=10, WY=100 and timeLeft=47.)
Repeat the above process (moving the cut from Y=0 upwards). When will the type of the area change? Clearly, this will happen whenever the cut passes through a vertex of the "good outcomes" polyhedron.
Now our goal will be to cut the polyhedron into pieces so that in each piece all cuts will have the same type. We can do this without even computing where the polyhedron's vertices are. How?
Note that all vertices of the "good outcomes" polyhedron had integer coordinates. Suppose that we make a horizontal cut at each integer Y. This will divide the polyhedron into WY pieces, each 1 unit tall. Clearly, there are no vertices of the polyhedron inside any of the pieces.
Now let's consider an arbitrary piece and take a closer look at the integral we are computing. Clearly, for the first case (area is a triangle) and the third case (area is all but a triangle)
area(WX,XZ,Y) is a quadratic function of Y.
For the second case (area is a trapezoid)
area(WX,XZ,Y) is a linear function of Y.
(For the two boundary cases area() is clearly a constant function.)
This means that in each of the pieces we are integrating either a constant, a linear, or a quadratic function.
And here comes the beauty. We don't have to know which case we integrate. The trick is to use Simpson's Rule to compute the value of the integral. For general functions Simpson's Rule is just an approximation of the integral, but for up to cubic polynomials the output is exact.
In our situation, the rule is almost unbelievably simple. For an at-most-cubic polynomial
f() we have: 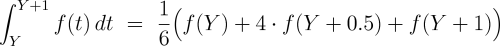
The complete code solving the general case is then just a few lines:
double cutAreas[] = new double[2*wait[0]+1];
for (int x=0; x<=2*wait[0]; x++)
cutAreas[x] = area(wait[1],wait[2],timeLeft-0.5*x);
double volume = 0.0;
for (int x=0; x<wait[0]; x++)
volume += (cutAreas[2*x] + 4*cutAreas[2*x+1] + cutAreas[2*x+2]) / 6;
for (int i=0; i<3; i++) volume /= wait[i];
return volume;
Amazing, isn't it?
