
|
Match Editorial |
Monday, March 6, 2006
Match summary
Despite SnapDragon's statement that he is out of practice, he won the Division 1 quite easily. Egor took second, especially thanks to his excellent time on the medium problem, and misof went home with bronze.
The Division 1 problem set was one of the easier ones, with 24 coders getting all three problems right.
Also the Division 2 problem set seemed to be pretty well balanced, with 16 coders solving the whole set. The top two places were taken by newcomers, ihi and Bel_Vit, rlblaster was third. We will be seeing them in Division 1 next time.
The Problems
FowlRoad

Used as: Division Two - Level One:
Value 250 Submission Rate 332 / 374 (88.77%) Success Rate 262 / 332 (78.92%) High Score Nitz for 245.18 points (3 mins 59 secs) Average Score 195.34 (for 262 correct submissions)
First of all, note that we may ignore the x coordinate of the chicken. The fact whether a segment of the path crosses the road depends only on the y coordinates of its endpoints.
Now, we may simplify the situation even more by subtracting roadY from all the coordinates in the chicken's path. With the new coordinates, we are interested in how many times the chicken crosses the x axis.
We can count this in a simple loop. All we have to do is to keep track of the side we were on, i.e., whether our last non-zero y coordinate was positive or negative.
Note that we may forget all the zeroes completely. For example, both the sequences { 3, 0, -2, 0, -3, -4, 0, 7 } and { 3, -2, -3, -4, 7 } cross the x axis twice.
C++ code:
int crossings(int roadY, vector <int> bobX, vector <int> bobY) {
int res = 0;
// compute the shifted coordinates
// at the same time, throw out all zeroes
vector<int> newY;
for (unsigned i=0; i<bobY.size(); i++)
if (bobY[i] != roadY)
newY.push_back( bobY[i]-roadY );
// now count the number of times we cross the x axis
for (unsigned i=1; i<newY.size(); i++)
if (newY[i] * newY[i-1] < 0) res++;
return res;
}
Abacus


Used as: Division Two - Level Two:
Used as: Division One - Level One:
Value 500 Submission Rate 285 / 374 (76.20%) Success Rate 200 / 285 (70.18%) High Score 250710 for 482.42 points (5 mins 27 secs) Average Score 329.29 (for 200 correct submissions)
Value 250 Submission Rate 355 / 360 (98.61%) Success Rate 331 / 355 (93.24%) High Score tomek for 246.41 points (3 mins 26 secs) Average Score 214.07 (for 331 correct submissions)
In this problem, there wasn't really anything to think about. The only problem was implementing the conversions between numbers and their graphical representation.
For the conversion in one direction we may use the index of the first dash in the string.
For the conversion in the other direction, it may be convenient to split it into two steps: first, split the number into digits, and then use the digits to generate the rows of the abacus.
C++ code:
vector <string> add(vector <string> original, int val) {
// convert the abacus into a number
int number = 0;
for (unsigned i=0; i<original.size(); i++) {
int digit = 9 - original[i].find("-");
number = 10*number + digit;
}
// add the requested value
number += val;
// convert the new number into digits
vector<int> digits;
for (unsigned i=0; i<original.size(); i++) {
digits.push_back( number % 10 );
number /= 10;
}
// bring the most significant digits to the beginning
reverse( digits.begin(), digits.end() );
// and create the new abacus
vector <string> res( original.size() );
for (unsigned i=0; i<original.size(); i++) {
res[i] += string( 9-digits[i], 'o' );
res[i] += string( 3, '-' );
res[i] += string( digits[i], 'o' );
}
return res;
}
SysFailure


Used as: Division Two - Level Three:
Value 1000 Submission Rate 54 / 374 (14.44%) Success Rate 28 / 54 (51.85%) High Score tomek_cn for 814.00 points (14 mins 16 secs) Average Score 559.27 (for 28 correct submissions)
The first step we can do to make our life easier is to pad the input array – if we surround it by zeroes, we won't have to worry about checking for the array's bounds when looking for clusters of ones.
In C++ this can be done as follows:
int R, C; // number of rows and columns
int critical(int n, vector <string> state) {
R = state.size(), C = state[0].size();
state.insert(state.begin(), string(C,'0'));
state.insert(state.end(), string(C,'0'));
for (int r=0; r<R+2; r++) state[r] = '0'+state[r]+'0';
// now the original array has coords [1..R] x [1..C]
// ... the rest of the code ...
}
The next logical step is to write a function that, given a map of the system, finds the size of the largest connected cluster of components.
This function can be implemented as a breadth/depth-first search in a graph, where the vertices are active components (ones in the matrix) and two vertices are connected if and only if they are adjacent.
C++ code of this function, implemented using BFS:
int R, C; // as above
// it's often useful to use constants to store valid moves
int dx[] = { -1, 0, 1, -1, 1, -1, 0, 1 };
int dy[] = { -1, -1, -1, 0, 0, 1, 1, 1 };
int getLargest(vector<string> state) {
int maxSize = 0;
// traverse a matrix
// each time we encounter a '1', we have a new cluster
// run BFS to find its size and change all its '1's into '0's
for (int r=1; r<=R; r++) for (int c=1; c<=C; c++)
if (state[r][c]=='1') {
int thisSize = 1;
state[r][c]='0';
queue<int> Q;
Q.push(r); Q.push(c);
while (!Q.empty()) {
// get the next vertex out of the queue
int x = Q.front(); Q.pop();
int y = Q.front(); Q.pop();
// process its neighbors
for (int d=0; d<8; d++) {
int nx = x + dx[d];
int ny = y + dy[d];
// [nx,ny] are the coordinates of our neighbor in direction d
// note that thanks to the padding [nx,ny] are always valid
if (state[nx][ny]=='1') {
state[nx][ny]='0';
thisSize++;
Q.push(nx); Q.push(ny);
}
}
}
maxSize = max(maxSize, thisSize);
}
return maxSize;
}
Now, using this function, solving the task is simple. If already in the input configuration all the clusters are too small, return -1. Otherwise, process the active components one by one, each time turn it off, check how the maximal cluster size changed, and turn it back on.
int critical(int n, vector <string> state) {
// ... we already saw a part of this function ...
int orig = getLargest(state);
if (orig < n) return -1;
int res = 0;
for (int r=1; r<=R; r++) for (int c=1; c<=C; c++)
if (state[r][c]=='1') {
state[r][c]='0';
int after = getLargest(state);
if (after < n) res++;
state[r][c]='1';
}
return res;
}
BobTrouble


Used as: Division One - Level Two:
Value 500 Submission Rate 178 / 360 (49.44%) Success Rate 71 / 178 (39.89%) High Score Egor for 457.60 points (8 mins 48 secs) Average Score 276.60 (for 71 correct submissions)
This problem stumped me for a while. I had to convince myself that a greedy approach will really work here. Let's start analysing this problem by drawing a few images.
Imagine a valid hierarchy tree, for example the one in the following image:
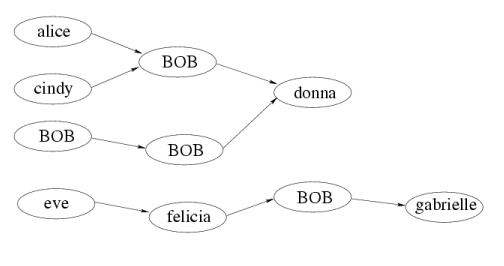
Now, the problem statement basically says the following: If somebody's boss is BOB, we may choose which of the BOBs it will be. The crucial observation leading to a solution is: We can choose the same BOB for all employees.
Why is this so? Suppose that we have a valid solution, and there is more than one BOB having some direct employees. Select any two such BOBs. If one of them is higher in the hierarchy than the other, we may move all employees of the "lower BOB" directly to the "higher BOB". The graph will clearly remain acyclic. The other situation is even simpler, if neither of the BOBs is reachable from the other, we may transfer the employees either way.
Using a finite number of such transformations we will always arrive into a situation when, except for at most one BOB, no BOBs have direct employees.
As an example, we can transform the above hierarchy into this one:
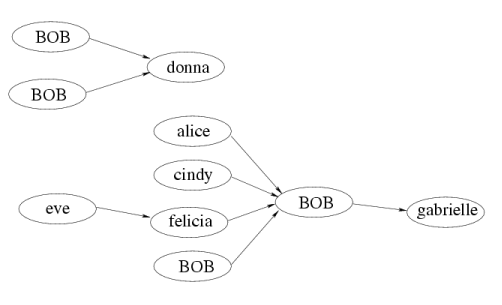
Let's repeat the result proved above: IF there is a valid solution, THEN there is one such that all employees whose boss is BOB are the direct employees of one and the same BOB. Thus we can check all posibilities for which BOB this is, and each time check whether the resulting graph is acyclic.
Once we find a valid hierarchy, we can count the number of bosses and output it. If no choice of the "king BOB" leads to a valid hierarchy, return -1.
As a curiosity, note that the problem could be solved without even mentioning the string "BOB" in your code. See Egor's solution as an example. The solution simply builds the hierarchy tree by doing a breadth-first search from *. This will automatically enforce that the "topmost" BOB is inserted into the hierarchy first, and all (some BOB)'s employees will later be inserted as his employees.
LongBlob

Used as: Division One - Level Three:
Value 1000 Submission Rate 99 / 360 (27.50%) Success Rate 76 / 99 (76.77%) High Score kalinov for 932.43 points (7 mins 45 secs) Average Score 650.03 (for 76 correct submissions)
We can rephrase the problem as follows: Given a grid, find a path such that:
- in each step, we can move one square in any of the four directions
- the total number of '1'-squares on the path mustn't exceed 4
- the ends of the path are as far apart (in Euclidean metrics) as possible
(As a hidden catch, note that the path may both start and end on a '1'-square.)
Now we clearly have a graph problem. What exactly is the graph? The squares will be vertices of the graph, edges will connect neighboring squares. If we want to enter a '1'-square, first we have to "turn it off". Therefore the "length" of an edge entering a square will be zero if the square is '0', one if the square is '1'.
Suppose we want a path that begins in the square [ax,ay] and ends in the square [bx,by]. How to check whether these squares can be connected by a valid path? Simply find the shortest path from [ax,ay] to [bx,by] in the graph constructed above. The length of this path (plus 1 if the starting square is a '1'-square) is the smallest possible number of '1's on a path from [ax,ay] to [bx,by].
In the SRM, I used Dijkstra's shortest path algorithm to compute the all-pairs shortest paths. Somewhat surprisingly, Floyd-Warshall's algorithm is fast enough, and leads to a pretty short implementation.
int dr[] = { -1, 1, 0, 0 };
int dc[] = { 0, 0, -1, 1 };
int dist[32][32][32][32];
double maxLength(vector <string> image) {
int R = image.size(), C = image[0].size();
// initialize the distance matrix to (0 or infinity)
memset(dist,0,sizeof(dist));
for (int ri=0; ri < R; ri++)
for (int ci=0; ci < C; ci++)
for (int rj=0; rj < R; rj++)
for (int cj=0; cj < C; cj++)
if (ri!=rj || ci!=cj)
dist[ri][ci][rj][cj] = 123456;
// for each vertex, set the lengths of edges into its neighbors
for (int ri=0; ri < R; ri++)
for (int ci=0; ci < C; ci++)
for (int d=0; d<4; d++) {
int rj = ri + dr[d], cj = ci + dc[d];
if (rj<0 || rj>=R || cj<0 || cj>=C) continue;
dist[ri][ci][rj][cj] = (image[rj][cj]-'0');
}
// Floyd-Warshall
for (int rk=0; rk < R; rk++)
for (int ck=0; ck < C; ck++)
for (int ri=0; ri < R; ri++)
for (int ci=0; ci < C; ci++)
for (int rj=0; rj < R; rj++)
for (int cj=0; cj < C; cj++)
dist[ri][ci][rj][cj] <?=
dist[ri][ci][rk][ck] + dist[rk][ck][rj][cj];
// process all pairs of vertices
// if there is a valid path between them, update the result
double res = 0.0;
for (int ri=0; ri < R; ri++)
for (int ci=0; ci < C; ci++)
for (int rj=0; rj < R; rj++)
for (int cj=0; cj < C; cj++)
if ( (image[ri][ci]-'0') + dist[ri][ci][rj][cj] <= 4)
res >?= hypot( double(ri-rj), double(ci-cj) );
return res;
}
