
|
Match Editorial |
Thursday, January 19, 2006
Match summary
In Division 1, the problemset turned out to be really hard, with nobody being able to solve all 3 problems (only misof, ploh and Petr were able to submit all 3 problems). Coders who solved 1000 point problem had occupied top 5 places. rem took the first place with only a little bit more than 150 points margin from marek.cygan, who finished fifth. misof, Revenger and ACrush took second, third and fourth places, respectively.
In Division 2, less than 30 coders was able to solve more than 1 problem. First timers DenRaskovalov and shell took first and second places and got nice 1906 and 1815 rating points, respectively. Ice-man took third place an was promoted to the top division.
Despite Petr's 19th place, Russia took the lead in the countries' rating for the first time ever. It's a fine landmark in the Russian history on TopCoder.
The Problems
DiagonalDisproportion

Used as: Division Two - Level One:
Value 250 Submission Rate 380 / 412 (92.23%) Success Rate 376 / 380 (98.95%) High Score cypressx for 249.61 points (1 mins 7 secs) Average Score 219.05 (for 376 correct submissions)
Diagonal disproportion of a square matrix can be calculated using the following
expression: 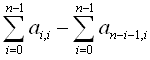 , where ai,j is
an element, located in i'th row and j'th column of the given matrix.
Result of the above expression can be easily computed using the following C++ code:
, where ai,j is
an element, located in i'th row and j'th column of the given matrix.
Result of the above expression can be easily computed using the following C++ code:
int getDisproportion(vector <string> a) {
int ret = 0;
for (int i = 0; i < a.size(); i++) ret += a[i][i] - a[i][a.size() - 1 - i];
return ret;
}
PowerSupply


Used as: Division Two - Level Two:
Used as: Division One - Level One:
Value 600 Submission Rate 90 / 412 (21.84%) Success Rate 18 / 90 (20.00%) High Score shell for 497.95 points (13 mins 26 secs) Average Score 329.00 (for 18 correct submissions)
Value 300 Submission Rate 216 / 299 (72.24%) Success Rate 115 / 216 (53.24%) High Score tomekkulczynski for 280.17 points (7 mins 40 secs) Average Score 192.11 (for 115 correct submissions)
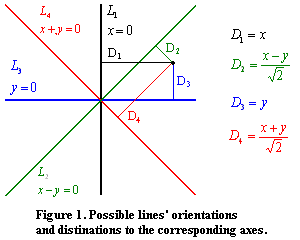
It's easy to notice, that we can consider only lines, which are D away from some consumer-point. So, to solve the problem it's enough to brute force all possible combinations of a consumer-point, and a line orienation, compute the answer for each such combination and choose the best. To compute the answer for particular combination we need to calculate how many consumer-points are located not farther than 2*D from the line, drawn through the chosen point with the chosen angle. Here we need to consider only points, located on the same side of the line. But how to determine a distance between point and a line, where line can be diagonal? To solve this sub problem we may compute the distances from each point to each of 4 axes, shown on figure 1. Having this values computed, we can easily determine a distance between any two points in rotated coordinate system.
Notice that distances from lines L1 and L2 may be squared to receive an integer values. C++ code follows:
int solve(vector <int> a, long long D) {
int ret = 0;
sort(a.begin(), a.end());
for (int i = 0; i < a.size(); i++) {
for (int j = i + 1; j < a.size(); j++)
if ((long long)(a[j] - a[i]) * (a[j] - a[i]) > D) break;
ret = max(ret, j - i);
}
return ret;
}
int maxProfit(vector <int> x, vector <int> y, int D) {
int ret = 0, n = x.size();
vector <int> a2(n), a4(n);
long long hvD = (long long) D * D * 4;
long long diagD = hvD * 2;
vector <int> a1 = x;
for (int i = 0; i < n; i++) a2[i] = x[i] + y[i];
vector <int> a3 = y;
for (int i = 0; i < n; i++) a4[i] = x[i] - y[i];
ret = max (ret, solve (a1, hvD));
ret = max (ret, solve (a2, diagD));
ret = max (ret, solve (a3, hvD));
ret = max (ret, solve (a4, diagD));
return ret;
}
See myprasanna's code as an example of short and elegant solution. It can be easily modified to operate with integer numbers.
FactorialGCD

Used as: Division Two - Level Three:
Value 1000 Submission Rate 171 / 412 (41.50%) Success Rate 12 / 171 (7.02%) High Score Ice-man for 988.92 points (3 mins 0 secs) Average Score 642.44 (for 12 correct submissions)
Let Pa! be a multiset of primes in prime-decomposition of a! and Pb be the same thing for b. For example, if a=4 (a!=4!=24) and b=150, then Pa! = {2,2,2,3} and Pb = {2,3,5,5}. What is the GCD(a!,b)? GCD(a!,b) is a product of all elements of PGCD(a!,b). And PGCD(a!,b) is the intersection of Pa! and Pb. But how can we find this intersection quick enough? Let's factorize number b on primes. Imagine we found that b ni times divides on some prime pi. Now we need to find out how many times number a! divides on pi. How to do it? As we know, a! = 1*2*...*(a-1)*a. Every number, that can be divided on pi can be represented as k*pi. a! contains only positive multipliers, so we may brute force k starting from 1. Let j = k*pi. For each j we need to realize how many times it can be divided on pi. In such manner we can calculate how many times a! divides on pi (let's call this value mi). We may stop this calculation as soon as mi becomes greater or equal to ni. This is a clean C++ implementation of the described algorithm:
int factGCD (int a, int b) {
int ret = 1;
for (int p = 2; (long long) p * p <= b; p++) if (b % p == 0) {
int d1 = 0;
for (; b % p == 0; d1++) b /= p;
int n = a, d2 = 0;
/// Another way to calculate how much time p divides (a!)
while (n > 0) d2 += (n /= p);
for (int i = 0; i < min(d1, d2); i++) ret *= p;
}
if (b != 1) if (b <= a) ret *= b;
return ret;
}
Pay attention to Ice-man's elegant solution.
FactorialTower

Used as: Division One - Level Two:
Value 600 Submission Rate 34 / 299 (11.37%) Success Rate 9 / 34 (26.47%) High Score ploh for 359.97 points (27 mins 23 secs) Average Score 283.47 (for 9 correct submissions)
Let's simplify the problem: let's compute the following expression: n!v mod m. At the first step we need to find n! mod m. How can we done it if 0 ≤ n ≤ 2147483647 and 1 ≤ m ≤ 40000? Notice, that if n ≥ m, then n! mod m = 0. And if n < m we can find n! mod m iteratively in no more than 40000 operations. C++ code follows:
// pay attention to the tricky case 0! mod 1 = 0 int u = 1 % m; if (n >= m ) u = 0; else for (int i = 2; i <= n; i++) u = (u * i) % m;
Thus, we have u = n! mod m. Now we need to find uv mod m. Notice, that value of ui mod m will be in range [0, m - 1] for any non-negative integer i. Imagine we are iterating i starting from 0. We'll receive following values: u0 mod m, u1 mod m, and so on. According to the pigeonhole principle, one of the values will repeat in no more than (m + 1) iterations. Consider the following example. Let u = 2, m = 56. The first 7 iterations are shown in the table:
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| ui mod m | 1 | 2 | 4 | 8 | 16 | 32 | 8 |
Here we have a cycle {8,16,32} and a precycle {1,2,4}. How it can help us to calculate uv mod m? Let the length of the cycle be L, and length of precycle be P. Notice, that if v ≤ P, then we can just take the value from our table for i = v. In the other case, v falls in the cycle, and we are interested in v mod L only. As soon as v mod L will have been calculated, we should just take the value from our table for i = P + ( L + v mod L - P mod L ) mod L. Thus, we reduced the "n! mod m = ?" problem to the "v mod L = ?" problem.
Let's go back to the original problem. Here we want to calculate (a0!^a1!^...^an-1!) mod m. Let a1!^...^an-1! = v. So, we have the problem that had just been discussed. "a0! v mod m = ?" problem can be reduced to "v mod L = ?" problem. v = a1!^...^an-1!, so we can solve "a1!^...^an-1! mod L" problem in the same manner.
Many coders has troubles determining if (ai+1!^ai+2!^...^an-1!) falls in a precycle or in a cycle when calculating the i'th stage of the tower. Idea is quite simple. Notice, that P (the precycle's length) certianly can't be greater than m. So, we can iteratively calculate (ai+1!^ai+2!^...^an-1!), and as soon as it reachs 40000, we can stop iterating. So, if (ai+1!^ai+2!^...^an-1!) ≥ 40000, we can be sure, that it falls into a cycle, but not precycle. We can use the following C++ code to precalculate neccessary values:
vector <int> a; // original vector a
int prec[51];
void precalc(void) {
prec[n] = 1;
// going through a tower from top to bottom
for (int i = a.size() - 1; i >= 0; i--) {
r = 1;
// calculating a[i]!
for (int j = 2; j <= a[i] && r < 40000; j++) r *= j;
// raising a[i]! to the a[i+1]! degree
if (r > 1) {
prec[i] = 1;
for (int j = 0; j < prec[i+1] && prec[i] < 40000; j++) prec[i] *= r;
} else prec[i] = r;
}
}
MikeMirzayanov used somewhat another approach to solve this problem. He didn't find a cycles iteratively in his solution.
SuspiciousStrings

Used as: Division One - Level Three:
Value 1000 Submission Rate 9 / 299 (3.01%) Success Rate 5 / 9 (55.56%) High Score rem for 565.80 points (30 mins 19 secs) Average Score 522.38 (for 5 correct submissions)
You was asked to find out how many strings of length n, composed only from lowercase letters, contains any strings from given set as substrings. For low n's this problem can be solved by dynamic programming. For each particular length from 1 to n we need to compute by how many ways we can reach each particaular state. Only difficulty is to realize what to be a states. Let we have only one string in the set. Let this string be "topcoder" and n=10. For length 2 there are 26*26 possible strings, but do we really interested that one of them is "ab", another is "xy" and so on? Because only substring that we are interested in is "topcoder", we only need to whatch for substring, which are a prefixes of "topcoder". So, all 26*26 string of length 2 divides in 3 categories: 1) "to" (prefix of length 2); 2) "t" (prefix of length 1); 3) all other (we can say that it's a prefix of length 0). So, if there is only one string in the set, state is a length of prefix of this string, which is equal to the suffix of the current part (first i characters) of the main string. In case of multiple strings in the set, we need to remember all possible prefixes of each of this stings. One important thing we need to not forget is that suffix of some prefix of one string may be equal to some prefix of another string. Example: set = {"topcoder","cost"}. Suffix "co" of "topco" (wich is a prefix of first string in the set) is equal to the prefix "co" of the second string. Each state, which describes a prefix, with a length equal to the length the string, would lead to to itself. In such way, in the end of our dynamic programing, answer for the problem would be a sum of values in all such states. Let impementation of states' manipulation be an exercise for you.
And now let's go back to our problem. Here n can be up to 2^31-1. So, dynamic programming, described above, doesn't give us enough quickness. Let's have a look on what happens on each step of our dynamic programming algorithm. Here on each step (remind, that step is a current length of main string) we are computing by how many ways we can reach every state. We are doing it using similar data from the previous step. At first, let's notice, that this "data" is a vector with length equal to the amount of possible different states. This length, in the worst case, can be up to 101 (last sample in problem statement is a such worst case). Let's call this vector as "states vector". Here we need to notice, that if we mark all elements of states vector as x's (x0,x1,x2 and so on), then each element of the new states vector will look like weighted sum of all elements of the previous states vector. So, we can build a matrix, and then, on each step, we need to just multiply previous states vector on this matrix to archive a new states vector. I think, that construction of this matrix is not a serious problem for topcoders, who are familiar with dynamic programming. Because we are multuplying current states vector on the same matrix on each step, the resulting states vector for n'th step can be archieved by multiplication initial vector (all elements of this vector must be zeroes, except for element, corresponding to the "zero prefix" state, which must be 1) on the described matrix raised in degree n. Last thing that we need to realize in order to solve the problem is that we may raise a matrix in degree n with O(log(n)) complexity. This algorithm is well known, and had been used in several problems on TopCoder. For example, see discussion of the Div 1 Hard problem in this editorial. And don't forget to take every value, you've computed, modulo 10000.
Revenger used a trie to build a matrix. His solution is an example of very clear impementation.
