
|
Match Editorial |
Wednesday, December 28, 2005
Match summary
Coders in Division 1 faced a tricky medium and a difficult hard that had only 3 correct submissions. The medium provided many challenge opportunities. Most notably, gevak earned 350 points which placed him 4th. Petr was the only coder to solve all 3, beating his nearest competitor by nearly 400 points. ploh came second with the help from 4 successful challenges. ACRush came third and walked away with an impressive +422 rating change, claiming he is ready to take a much higher ranking.
In Division 2 the battle for top spot centered around solving the hard. guanyxcn finished first by more than 300 points. Second and third belonged to LampJinn and amarkovits respectively. Have a happy New Year and see you all in 2006!
The Problems
UniqueDigits

Used as: Division Two - Level One:
Value 250 Submission Rate 328 / 372 (88.17%) Success Rate 313 / 328 (95.43%) High Score FangLiu for 248.61 points (2 mins 7 secs) Average Score 203.90 (for 313 correct submissions)
This problem asked us to find numbers that do not have any repeating digits. We iterate through each number from 1 to n - 1. For each number, we use an array seen that stores whether a digit has occurred in that number. Iterating through each digit, if seen[currentDigit] is true then currentDigit has already occurred and so we do not count this number. Otherwise, we set seen[currentDigit] to true and continue the search. If we successfully reach the end of the search we update the count. Java code follows:
public int count(int n)
{
int count=0;
for (int i = 1; i < n; i++)
{
String num=""+i;
boolean[] seen=new boolean[10];
boolean ok=true;
for (int k = 0; k < num.length(); k++)
{
if (seen[num.charAt(k) - '0']) ok=false;
else seen[num.charAt(k) - '0']=true;
}
if (ok) count++;
}
return count;
}
CompletingBrackets


Used as: Division Two - Level Two:
Used as: Division One - Level One:
Value 500 Submission Rate 282 / 372 (75.81%) Success Rate 167 / 282 (59.22%) High Score palmcron for 494.15 points (3 mins 6 secs) Average Score 387.63 (for 167 correct submissions)
Value 250 Submission Rate 298 / 302 (98.68%) Success Rate 257 / 298 (86.24%) High Score antimatter for 248.75 points (2 mins 1 secs) Average Score 225.67 (for 257 correct submissions)
First of all, we observe that we only need to add ‘[‘ to the beginning and ‘]’ to the end. We let left and right be the number of brackets that need to be added to the beginning and end respectively. Iterating through text, if the current character is '[' then we have started a new [] pair, so we increment right. However, if the current character is ']' then we have either terminated a [] pair (so decrement right) or have met an extra ']' in which case we increment left. Now that the hard work has been done, we use two for loops to add the required brackets:
public String complete(String text)
{
int left=0, right=0;
for (int i = 0; i < text.length(); i++)
{
if (text.charAt(i)=='[') right++;
else
if (right>0) right--;
else left++;
}
for (int i = 0; i < left; i++) text='['+text;
for (int i = 0; i < right; i++) text+=']';
return text;
}
The constraints for this problem were low enough for a more brute-force
approach to work too.
We can keep adding brackets one by one and terminate as soon as the
series is complete. This
was used during competition by sql_lall.
GroupingNumbers


Used as: Division Two - Level Three:
Value 1000 Submission Rate 61 / 372 (16.40%) Success Rate 18 / 61 (29.51%) High Score TN_PKU for 926.84 points (8 mins 6 secs) Average Score 531.33 (for 18 correct submissions)
Originally this problem was intended to be harder with the number of elements up to 50. However, this proved to be too difficult and so the number of elements was reduced to 9. With just 9 elements we can solve this problem with brute force. The easiest way to do this (although not very efficient) is to generate all the permutations and choose the ones with exactly groups number of cycles. To count the number of cycles in a permutation we do the following. Starting with the first element, iterate through the cycle marking each element used. If we see an element for the second time then we have reached the end of the current cycle. We then find the next available element and repeat the same process until all elements have been used. Meanwhile, we keep track of the lowest and highest averages, which are used to update the best difference. Here is the code:
public double minRange(int[] numbers, int groups)
{
double best=Integer.MAX_VALUE;
int[] a=new int[numbers.length];
for (int i = 0; i < a.length; i++) a[i]=i;
do
{
int cycles=0, n=0, cur=0, total=0;
double min=Integer.MAX_VALUE, max=-1;
boolean[] used=new boolean[a.length];
while(true)
{
used[cur]=true;
total+=numbers[cur];
cur=a[cur];
n++;
if (used[cur]) //end of cycle
{
min=Math.min(min,total*1.0/n);
max=Math.max(max,total*1.0/n);
cycles++;
if (cycles > groups) break;
n=0;
total=0;
//find start of next cycle
for (cur = 0; cur < a.length && used[cur]; cur++);
if (cur==a.length) break; //all elements used
}
}
if (cycles==groups) best=Math.min(best,max-min);
}
while(nextPermutation(a));
return best;
}
My intuition tells me that this problem is also solvable in its original
format, so please
post your solutions in the forum.
GridCut


Used as: Division One - Level Two:
Value 500 Submission Rate 271 / 302 (89.74%) Success Rate 93 / 271 (34.32%) High Score tmyklebu for 484.42 points (5 mins 7 secs) Average Score 316.13 (for 93 correct submissions)
This problem was not too hard, but rather tricky. There are two things we can do to minimize the length of the cut: use edges as much as possible and cut out rectangles, since they have the smallest perimeter for a given area. The final shape will always be either a rectangle or a rectangle with an extra (incomplete) row of cells. We align the base of our rectangle with one of the edges, say the horizontal. We can then calculate its height and hence its cut length. To find the best solution we iterate through all the possible bases w.
This is not necessary though, because the problem can be solved in constant time (assuming we can find the square root of a number in a constant time). To show the solution, lets consider 2 different cases.
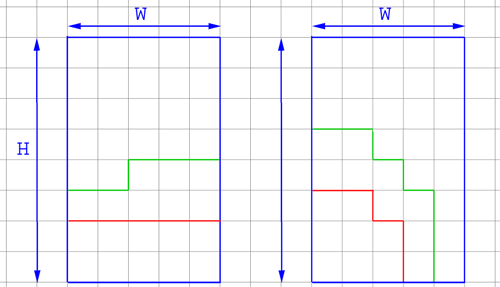
There were two major causes for failure. Some solutions failed because they did not try to align the base with the vertical edge. Others failed to notice that cutting out n cells is equivalent to cutting out (width*height–n) cells. It turns out that a very similar problem was used in 2003 TCCC International Round. Interestingly, the success rate for that problem was only 6%.
DrawPlanar

Used as: Division One - Level Three:
Value 1100 Submission Rate 16 / 302 (5.30%) Success Rate 3 / 16 (18.75%) High Score Petr for 482.80 points (47 mins 40 secs) Average Score 473.92 (for 3 correct submissions)
This problem was written by lbackstrom.
Despite being one of the most difficult problems during the last few months, DrawPlanar didn’t require any complicated algorithm. A brute-force with pruning mixed up with basic geometrical formulas was enough to solve this problem. On the other hand, coders needed to put some effort to make their solutions run in time.
The basic algorithm for this problem is relatively simple. Taking into account the maximal area can’t be more than 15, we are able to check all possible return values. For each such value, we try to fit the graph into each of the rectangles with area equal to the value. We return this area if succeeded, or continue to the (value + 1) otherwise. To check whether the graph fits in a given rectangle, we iterate through all vertices of the graph, trying to put each of them to every non-occupied cell. At every step, we check whether the new vertex will force graph edges to intersect (obviously, we need to check only the edges incident with this vertex vs all the edges we put earlier). Depending on whether at least some edges intersect, we either continue to the next vertex or try another position for the current one. Pseudo-code follows:
int minArea(String[] graph) {
.....
(0) do some preprocessing here
(1) int area = 0
(2) Check if the graph can be arranged in a line
(3) area = 1
(4) while (true) {
(5) for (int i = 1; i * i <= area; i++)
(6) if (area % i == 0 && fits(i, area / i, 0))
(7) return area;
(8) area++;
}
}
boolean fits(int W, int H, int vertex) {
(1) if (vertex == graph size) return true;
(2) for (int i = 0; i <= W; i++)
(3) for (int j = 0; j <= H; j++)
(4) if (!occupied[i][j] && neither edges intersect)
(5) return fits(W, H, vertex + 1);
(6) return false;
}
Though such rough approach will be timing out on some input graphs, there are a lot of possibilities to optimize it. Some of them are listed below:
Formulas and algorithms for line intersection can be found in Geometry Concepts Tutorial by lbackstrom. More info about planar graphs can be found here.
