
|
Match Editorial |
Saturday, December 17, 2005
Match summary
With 963 registrants, participants were bound to get a run for their money in both divisions. Division 1 coders were greeted by a complimentary 250 only to face a tricky 500 and a hard-to-code 1000. In the end, antimatter took the win with the help of two challenges, with misof and krijgertje (our newest target) closely in second and third, respectively.
In division 2, more than 200 coders solved both of the first two problems, but only 10 got the third one right. Newcomer Rocking had the highest score with 3 challenges for an impressive debut rating.
The Problems
SandwichBar

Used as: Division Two - Level One:
Value 250 Submission Rate 412 / 499 (82.57%) Success Rate 336 / 412 (81.55%) High Score N][M for 247.38 points (2 mins 55 secs) Average Score 200.25 (for 336 correct submissions)
In the problem we are asked to find the first sandwich wanted for which all ingredients are in the list of available ingredients. The solution comes down to some string parsing and simple logic. Here is an example of how the problem can be solved in Java:
public int whichOrder(String[] available, String[] orders) {
Set<String> s = new TreeSet();
for (int i = 0; i < available.length; i++)
s.add(available[i]);
for (int i = 0; i < orders.length; i++) {
boolean isok = true;
String[] p = orders[i].split(" ");
for (int j = 0; j < p.length; j++)
isok &= s.contains(p[j]);
if (isok) return i;
}
return -1;
}
C++ coders who don't know how to use istringstreams were at a slight disadvantage for not having a straightforward string tokenizing routine. Here's how one could have used istringstreams to get the job done:
int whichOrder(vector <string> available, vector <string> orders) {
for ( int i=0; i<(int)orders.size(); ++i ) {
istringstream iss( orders[i] );
string s;
bool ok = true;
while ( iss >> s )
if ( find( available.begin(), available.end(), s ) ==
available.end() )
ok = false;
if ( ok )
return i;
}
return -1;
}
RogersPhenomenon


Used as: Division Two - Level Two:
Used as: Division One - Level One:
Value 500 Submission Rate 402 / 499 (80.56%) Success Rate 312 / 402 (77.61%) High Score jueyey for 497.87 points (1 mins 51 secs) Average Score 380.53 (for 312 correct submissions)
Value 250 Submission Rate 416 / 419 (99.28%) Success Rate 352 / 416 (84.62%) High Score antimatter for 248.91 points (1 mins 53 secs) Average Score 219.40 (for 352 correct submissions)
After realizing what's going on, it should be obvious that this is a pretty simple simulation problem. For each number in both of the sets, we have to check if moving it to the other set will increase the means of both sets. Checking can be done the straightforward way (moving then comparing means), or we can note that the source set's mean will increase if the number moved is less than the current mean, and that the destination set's mean will increase if the number moved is greater than its mean.
Comparing fractions is best done using cross-multiplication so we avoid the use of doubles, although in this problem you were safe using doubles as well (because the difference between denominators of the fractions compared is always exactly one, which makes it impossible for floating-point imprecision to wreak havoc upon calculations).
Many coders got unsuccessful challenges expecting solutions to crash with a divide-by-zero error. However, IEEE floating-point representations (floats and doubles) handle such cases silently with special values: dividing a non-zero double by zero yields the special value infinity (positive or negative), while dividing a zero by zero yields NaN (not-a-number). NaNs behave somewhat awkwardly because every comparison involving them is false (even comparing two NaNs for equality), which stumped challengers.
UnionOfIntervals

Used as: Division Two - Level Three:
Value 1000 Submission Rate 80 / 499 (16.03%) Success Rate 10 / 80 (12.50%) High Score Zephyrzzz for 599.57 points (27 mins 25 secs) Average Score 489.01 (for 10 correct submissions)
The problem asks us to find the n-th smallest number in a (potentially huge) list of integers, which is given as a union of intervals (numbers may appear more than once in the resulting list). Most solutions failed on large cases either because of timeout or overflow.
There are at least three different approaches to solving this problem. One of them is intersecting the intervals repeatedly to get a list of mutually disjoint intervals, which can then be sorted and processed, another is using a sweep-line style algorithm, processing the intervals left to right using a priority queue of events. I will describe the third approach in detail.
Observe that it's possible to quickly count how many numbers in the list are less than some chosen number X (by iterating through all of the intervals). Now, if this number is greater than n, the solution is certainly smaller than X. Similarly, if this number is less than or equal to n, the solution is greater than or equal to X. This ought to be enough to hint at a solution based on binary search. Here is how it can be implemented in Java:
public int nthElement( int[] lowerBound, int[] upperBound, int n )
{
int lo = Integer.MIN_VALUE, hi = Integer.MAX_VALUE;
while ( lo < hi ) {
int X = (int)( ((long)lo+hi+1)/2 );
long count = 0;
for ( int i=0; i<lowerBound.length; ++i ) {
if ( X >= lowerBound[i] && X <= upperBound[i] ) {
// part of interval i is less than X
count += (long)X - lowerBound[i];
}
if ( X >= lowerBound[i] && X > upperBound[i] ) {
// all numbers in interval i are less than X
count += (long)upperBound[i] - lowerBound[i] + 1;
}
}
if ( count <= n ) lo = X;
else hi = X-1;
}
return lo;
}
As with all binary search solutions, you needed to carefully implement it and cast to a larger integer type in the appropriate places to avoid overflow because of the extreme numbers in the calculations.
AirlinerSeats

Used as: Division One - Level Two:
Value 500 Submission Rate 331 / 419 (79.00%) Success Rate 170 / 331 (51.36%) High Score gagik for 480.36 points (5 mins 47 secs) Average Score 289.29 (for 170 correct submissions)
Like with many problems that can be solved with a greedy approach, there is also a pretty dynamic programming solution hidden somewhere beneath. In this problem, the airplanes used were pretty wide so any dynamic programming approach in quadratic (or worse) time was doomed to time out. Hopefully, not many coders were too focused on finding the right DP solution.
Consider the following greedy algorithm (assume a row filled with aisles at the beginning): proceed from left to right and place seats in the pattern seat-aisle-seat: S.SS.SS.SS.SS.SS. ... If we run out of seats before reaching the end of the row, optionally reverse the arrangement and return it. Otherwise, proceed from right to left, filling in aisles with the remaining seats.
This is all there is to the solution, and the code is also pretty short. In case you're not sure if this is working, you can try it out on a few examples. In order to prove the algorithm, we can argue that:
- At any point in the algorithm, the current arrangement always has the maximum number of aisle seats (for the number of seats placed so far).
- There is no lexicographically smaller arrangement with the same number of aisle seats.
In the first part of the algorithm (before we reach the end of the row), all seats placed are aisle seats so we can't do better than that (property 1 is satisfied). Also note that this arrangement uses the least amount of space to place that number of aisle seats, since each aisle is used to make exactly two seats aisle seats. Hence, when we reverse this arrangement, we'll get the arrangement with the maximum possible number of aisles (dots) on the left, which is the lexicographically smallest arrangement (property 2 is satisfied).
A special case is when only one seat is placed at the end, instead of the S.S triplet. For example, when width=4 and seats=3, the arrangement generated is S.SS, but this is lexicographically smaller than SS.S. Many coders missed this case and their solution was brought down by a similar case in system tests, where width=11 and seats=8.
If there are still seats left over after the first, we proceed with the second part of the algorithm. In order to maintain property 1, we now need to place seats so as to revert as few as possible aisle seats back to ordinary status. Recall that all seats currently in the arrangement are aisle seats. There are really three possible ways our current arrangement can look like:
- S.SS.S … S.SS : each seat we put will make two previously aisle seats ordinary again, there's not much we can do about this. If we place seats from right to left, we'll get the lexicographically smallest arrangement.
- S.SS.S … S.SS. : placing a seat in the rightmost position makes only one aisle seat ordinary, so we do that. After that, we're basically left with the above situation.
- S.SS.S … S.SS.S : same as in the first case.
Thus, it is always optimal to fill seats in right-to-left order, as we claimed in the algorithm.
It was also possible to generate only the first and last 50 characters of the arrangement, but it was probably easier to generate the entire string, then return as appropriate.
There are other greedy approaches that will work, but the above proof implies the greedy choice and optimal substructure properties that are necessary for any problem to be solved using a greedy algorithm. For more information on greedy algorithms, read supernova's article Greedy is good.
SafeJourney

Used as: Division One - Level Three:
Value 1000 Submission Rate 24 / 419 (5.73%) Success Rate 10 / 24 (41.67%) High Score krijgertje for 593.00 points (27 mins 57 secs) Average Score 472.83 (for 10 correct submissions)
Most division 1 coders can probably recognize a shortest-path problem when they see it: split the grid into width × length unit cells (vertices), put an edge of weight 0 between every two adjacent cells which aren't separated by a road and an edge of weight 1 when there is a road in between. The problem is that width and length can both go up to 2 billion, which gives 4∙1018 vertices in total. No shortest path algorithm can handle graphs of this magnitude so we have to resort to a trick.
With the relatively small number of roads (the input format allowed for no more than 300 vertical and 300 horizontal roads), there will surely be a lot of free space in the plane. Consider the following two cases:
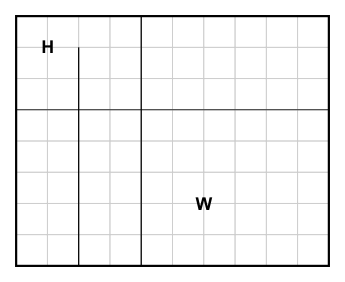 |
and | 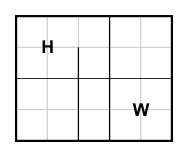 |
These two cases have the same solution, which is no coincidence. However, the latter case is clearly better to us: we are left with a smaller grid for our shortest-path algorithm to work on. In fact, we can transform any grid to a (usually) much smaller grid that really represents the same case. To do this, we proceed from left to right in the source grid and assign increasing x-coordinates (starting from 0) wherever there is some object (boundary, home, work, or road endpoint) at that coordinate.
In the example above, we assign x-coordinates 0, 1, 2, 3, 4 and 5 in the new grid to x-coordinates 0 (boundary), 1 (home), 2 (road), 4 (road), 6 (work) and 10 (boundary) in the old grid. We proceed in a similar fashion for y-coordinates. What we're left with is a grid composed of at most O(H∙V) unit cells, where H and V are the numbers of horizontal and vertical roads, respectively. Coordinate compression is a technique often needed in problems featuring huge (usually discrete) grids to be worked on, such as this one.
After we've compressed the grid and constructed a graph, we need to run a shortest-path algorithm. Not all choices will do, since the graph can get quite large (system tests included a grid of size 622 × 622). It was possible to use Dijkstra's algorithm (as bmerry did), implemented with time complexity O(E log V), but all other passing solutions used a modification of breadth-first search, which runs in O(E) time.
Breadth-first search is usually used on unweighted graph, but we can use it on 0-1 graphs as well, by using a deque (double-ended queue) instead of a regular queue: any time we expand over an edge of weight 0, we insert the neighbour vertex at the front on the queue. When we use an edge of weight 1, we push the vertex at the end of the queue. This way, closer vertices will be processed before the farther ones. Observe that a vertex may be pushed on the deque twice (first via a 1-edge, then a 0-edge before the first one is processed). However, the implementation will be careful to only process the first copy and in the worst case, this only adds a factor of at most two to the runtime.
