
|
Match Editorial |
Wednesday, August 4, 2004
Match summary
After winning Division II on Saturday, TopCoder member -_- went two for two, winning Division I by a margin of over 140 points. -_- is now red, with a ranking of 2378 after competing in only two matches. SnapDragon came in second, the only other coder to solve all three problems. Rounding out the top five were Eryx, jms137, and radeye.
In Division II, anikov took the title by a margin of almost 200 points of alsomagic. These top two were the only coders to solve all three problems. gmenhorn, ToadX, and lujo (the only other coder to solve the 1000-point problem) took the 3rd, 4th, and 5th spots.
The Problems
Bits
Used as: Division Two - Level One:
Value 250 Submission Rate 174 / 181 (96.13%) Success Rate 154 / 174 (88.51%) High Score coshx for 249.65 points (1 mins 4 secs) Average Score 230.11 (for 154 correct submissions)
With b bits, computers can represent numbers in the range 0 to 2b-1. So, this problem is asking you to find the smallest b such that 2b > n. This can be done by counting how many times you must divide n by 2 (throwing away the remainder) until you get zero:
int b = 0;
while (n > 0) {
n = n / 2;
b++;
}
return b;
Others solved the problem by using Java's Integer.toBinaryString() method (or a similar function from their personal library of pre-written code), and returning the length of the string.
OmahaLow
Used as: Division Two - Level Two:
Used as: Division One - Level One:
Value 500 Submission Rate 101 / 181 (55.80%) Success Rate 52 / 101 (51.49%) High Score gmenhorn for 389.33 points (16 mins 8 secs) Average Score 238.24 (for 52 correct submissions)
Value 250 Submission Rate 164 / 176 (93.18%) Success Rate 136 / 164 (82.93%) High Score SnapDragon for 242.41 points (5 mins 3 secs) Average Score 169.67 (for 136 correct submissions)
Many people tried to solve this problem in clever ways, but this problem is most easily solved by brute force. Five nested loops can easily give you all possible combinations of 3 of the five shared cards and 2 of the player's four cards:
for (int s1=0; s<5; s1++)
for (int s2=s1+1; s2<5; s2++)
for (int s3=s2+1; s3<5; s3++)
for (int p1=0; p1<4; p1++)
for (int p2=p1+1; p2<4; p2++) {
string hand;
hand += sharedCards[s1];
hand += sharedCards[s2];
hand += sharedCards[s3];
hand += sharedCards[p1];
hand += sharedCards[p2];
...
}
Inside the loop, you sort the characters in the string (high to low), make sure it's a legal low hand, and then check if it's lower than the lowest low hand you've seen so far.
That's not to say that there is anything wrong with clever solutions. SnapDragon made use of STL sort() and next_permutation() methods and noticed that a simple string comparison was sufficient to test of one hand was lower than another, and coded up an elegant solution in just over 5 minutes (the fastest time for this problem).
Untypeset
Used as: Division Two - Level Three:
Value 1000 Submission Rate 5 / 181 (2.76%) Success Rate 3 / 5 (60.00%) High Score anikov for 585.77 points (28 mins 33 secs) Average Score 481.73 (for 3 correct submissions)
This problem was actually quite straightforward, and the example in the problem statement basically spelled out how to solve it. But, as evidenced by only 3 successful solutions (out of 5 submissions total), the implementation was a bit on the tricky side.
This problem is best solved by recursion. You write a recursive function that takes an array of strings as input and returns an integer. This function determines if the input is an addition, division, or integer constant. If the input is an integer constant, the function simply returns the value of that integer. Otherwise, the input is addition or division, and the function breaks the array of strings into two subexpressions (the left and right for addition, or the top and bottom for subtraction). It then recursively calls itself on the two subexpressions, adds or divides the two results, and returns that value.
To determine if the input is an integer, addition, or subtraction, loop over all the rows and see if any contain only '-' characters. If so, then it is division. Otherwise, loop over all columns and see if any contain a row of only spaces except for a single '+' character. If so, then it is addition. Otherwise, since the input is guaranteed to be legal and well-formed, it must be an integer constant.
Dealing with the spaces inserted around subexpressions can be done at the top of the recursive function, by simply trimming all blank rows and columns along the 4 edges.
See anikov's solution for an example of a nice implementation of this solution.
SensorGrid
Used as: Division One - Level Two:
Value 500 Submission Rate 83 / 176 (47.16%) Success Rate 43 / 83 (51.81%) High Score Ruberik for 434.69 points (11 mins 22 secs) Average Score 298.90 (for 43 correct submissions)
People tried many approaches to solving this problem, from a brute-force O(n^5) search to some very clever algorithms. It was my intention that the input size would be too large for O(n^5) searches, but they squeaked by in the time allowed. Computers are just too fast these days...
A helpful observation is that the largest rectangle will be bounded on all four sides by a defective sensor or the edge of the grid. The O(n^5) search loops over all points (and relevant edge) for each of the 4 sides. Then with a 5th loop, it checks that no other points are inside this rectangle. If there are none, then it checks if this rectangle is larger that the largest rectangle found so far (or higher if they have the same area, or further to the left if they have the same area and vertical position, or wider if they have the same area and upper-left position). For an example of this approach see Ruberik's solution, which he coded in under 11 and a half minutes for the fastest time on this problem.
jms137 improved this search to O(n^4) with three loops to bound the left, right, and top sides of the rectangle, and then a fourth loop to find the highest point inside this region to give the bottom edge.
-_- and SnapDragon both implemented elegant O(n^3) solutions which are worth taking a look at. Cosmin.ro claims to have an O(n^2) solution, which I hope he will share with us in the forums.
HexagonIntersections
Used as: Division One - Level Three:
Value 1100 Submission Rate 6 / 176 (3.41%) Success Rate 2 / 6 (33.33%) High Score -_- for 485.17 points (47 mins 13 secs) Average Score 407.58 (for 2 correct submissions)
This problem was simple to state, but the solution was elusive. When dealing with geometry, you should be very worried about using floating-point numbers in your solution, as they can lead to numerical inaccuracies. You should be even more worried when you see a problem that requires some exact math as this one does: you must count hexagons if the line segment passes through the interior, but not if it only intersects an edge or a corner. Nonetheless, -_- got his solution to work using floating point for the fastest time for this problem. On the other hand, SnapDragon, the only other coder to solve this problem, used integer math. That is what I had in mind for this problem, and I will describe how this works below.
The first important thing to realize is that you can convert the hexagonal grid so that the corners lie on integer coordinates. An affine transformation (translation, scaling, rotation, shearing, and reflection) applied to any two-dimensional figure will preserve straight lines. That is to say, you can draw a straight line on a hexagonal grid, and then rotate, scale, and shear the image all you want, and the hexagons will still have 6 straight edges, and the line will still be straight and pass through the same hexagons as it did before. By scaling the grid vertically and shearing it horizontally, you can get an equivalent grid shown in the figure below:
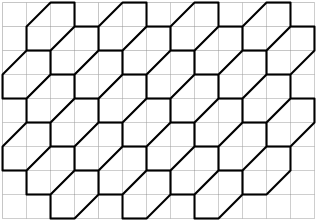
The transformation from coordinates identifying hexagon centers given in the problem to coordinates on this grid is:
x' = x + y
y' = 2*y - x
To simplify things a bit, you can first translate the line so that it starts at the origin (by subtracting (x0,y0) from (x1,y1)). Then, using symmetry, you can reduce the range of directions of the line to limit the number of cases you need to consider. In my solution, I rotated the line so that it would always point in the the range shown by the blue arrows in the figure below.
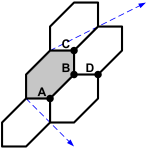
Once everything is set up, you start at the origin and walk from hexagon to hexagon until you reach the destination. Deciding which hexagon to move to can be done by checking what sides of the current hexagon's corners the line passes. Referring to the figure above:
- If the line passes to the right (or clockwise) of point A, you step to the hexagon below.
- Otherwise, if the line passes to the right of point B, you step to the hexagon diagonally down and to the right. (Note, this includes the case of the line passing through point A.)
- Otherwise, if the line passes to the left (counter clockwise) of point C, you step to the hexagon above.
- Otherwise, if the line passes to the left of point B, you step to the hexagon above and to the right. (Note, this includes the case of the line passing through point C, and makes use of the limited range of directions for the line.)
- Otherwise, the line passes through point B you then check it against point D:
- If the line passes to the left of point D, you step to the hexagon above and to the right.
- Otherwise, if the line passes to the right of point D, you step to the hexagon below and to the right.
- Otherwise, the line passes through point D and you step to the hexagon to the right of point D (not shown).
Note that the range of possible directions for the line limit the number of cases you need to consider to those cases above. Testing which side of a point the line passes is done with a two-dimensional cross product:
c = (x1 * corner_y) - (y1 * corner_x)If c is negative, the line passes to the left, if c is positive the line passes to the right, and if c is zero, the line passes through the point.
