Match Editorial

Three-dimensional geometry is poison to some. It was balm for tjq, who solved all three Division One problems in little more than an hour to win the latest single-round match. Hot on his heels came haha, finishing a fraction of a point behind. "To compute the distance between a line segment and a point in space is child's play," said the top two in a fictitious post-match interview. "You just derive a whatsit and squeeze it through a thingummybob." Klinck, who had won third place, chimed in, "Then you twiddle the didgeridoo, and you're done!" So it's that easy.

In Division Two, coders recoiled from the geometric overtones of the hard problem like vampires from a garlic plantation. It was either that or the funky recursion, but not one correct submission came in. Even so, python55 had cause to celebrate after his eighteenth competition, winning the division and finally earning a ticket to the major league. Also enduring the pain were dontian and sean_henderson, who both came within thirty points of first place.

The Problems

Value	250
Submission Rate	200 / 212 (94.34%)
Success Rate	149 / 200 (74.50%)
High Score	Tantalus for 245.36 points (3 mins 55 secs)
Average Score	206.71 (for 149 correct submissions)

Dinky fish breed with clockwork regularity: at the end of every month, each male-female couple produces a pair of offspring, one of each sex. Given the current population of a fish tank and the tank capacity in liters, we are to calculate the number of months that elapse before there is fewer than half a liter per dinky fish.

Since the greatest allowable capacity is one million liters and the fish population doubles every month, the tank will soon become crowded. Simulation is recommended for a system of such brief duration. One way to simulate the monthly population increase is to write a loop, but I prefer recursion, where one writes a function that calls itself. This is an especially convenient approach in cases where the state of a system in the current time-step is defined as a function of its state in the previous time-step.

The key observation here is that the number of couples is the lesser of the number of males and the number of females. This number, in turn, is exactly the size of the population increase in males and in females.

def dinky(capacity, male, female):
   if (male+female > 2*capacity):
      return 0
   if (female < male):
      inc = female
   else:
      inc = male
   return 1 + dinky(capacity, male+inc, female+inc)

To avoid dealing with floating-point numbers, we double the tank capacity and then pretend that each dinky fish requires a full liter.

Value	500
Submission Rate	97 / 212 (45.75%)
Success Rate	16 / 97 (16.49%)
High Score	pyton55 for 319.05 points (24 mins 32 secs)
Average Score	266.09 (for 16 correct submissions)

Value	250
Submission Rate	164 / 176 (93.18%)
Success Rate	68 / 164 (41.46%)
High Score	tomek for 227.87 points (9 mins 1 secs)
Average Score	158.02 (for 68 correct submissions)

Given a corpus of spam messages, we are to determine whether at least 75% of the token set derived from a fresh email message appears in the spam corpus. There are two hurdles to clear in this problem. First, we must extract tokens from an email message, and second, we must treat the resulting tokens as a set with unique members.

Many languages, including Java, offer powerful libraries that will accomplish both tasks with a line or two, leaving little more than a pair of nested loops to code. If we have access to high-level parsing and hashing functions, a solution looks something like the following.

def filter(spam, mail):
   spam_hash = {}
   for message in spam:
      for tok in re.findall("[a-zA-Z]+", message.lower()):
         spam_hash[tok] = 1
   ret = []
   for i in range(len(mail)):
      message_hash = {}
      ct = 0
      for tok in re.findall("[a-zA-Z]+", mail[i].lower()):
         if (not message_hash.has_key(tok) and spam_hash.has_key(tok)):
            ct = ct+1
         message_hash[tok] = 1
      if (4*ct/3 >= len(message_hash.keys())):
         for tok in message_hash.keys():
            spam_hash[tok] = 1
      else:
         ret.append(i)
   return ret

Notice that we can use an integer calculation to determine whether the 75% threshold has been met. We must not neglect to render messages in lowercase or to expand the set of spam tokens whenever a new piece of spam is identified.

Programmers who don't have a regular-expression engine on hand can write their own tokenizing function.

def tokenize(message):
   ret = []
   tok = ""
   for c in message:
      if (c in "abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ"):
         tok = tok+c
      else:
         if (tok != ""):
            ret.append(tok)
         tok = ""
   if (tok != ""):
      ret.append(tok)
   return ret

      if (c in "abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ"):

      alpha = "abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ"
      found = 0
      for i in range(52):
         if (alpha[i] == c):
            found = 1
      if (found == 1):

The presence of a token in a token set can be determined in like fashion. Instead of a hash, then, we can use an ordinary list and a single loop.

Value	1000
Submission Rate	14 / 212 (6.60%)
Success Rate	0 / 14 (0.00%)
High Score	null for null points (NONE)
Average Score	No correct submissions

Given three consecutive readings from a radar installation that plots the locations of flying objects once per second, we are asked to consider the possibility that every object is traveling in a fixed direction at constant speed. If the data unambiguously lead to this conclusion, we are to calculate the speed of each object.

Since the readings are taken at one-second intervals, the speed of an object is trivially obtained from the distance between two consecutive radar-blip locations. What is less trivial to determine is which radar blips are, in fact, consecutive readings of the same object. Let us begin by computing the distance and direction—or, equivalently, the displacement vector—between a point from the first interval and a point from the second. The displacement vector from point (x0,y0) to point (x1,y1) is (x1-x0,y1-y0).

Now consider the displacement vector from the second point to some point in the third interval. If the two displacement vectors are identical, then the three points potentially belong to an object traveling in a straight line at constant speed. It is also possible that we have inferred a pattern where there is none, since the points may belong to different objects. We can, nonetheless, assume for the time being that we have identified a single object traveling in the desired fashion, and we proceed to look for further equalities between displacement vectors that span (a) the first and second readings and (b) the second and third readings while (c) hinging on the same point in the middle.

If we are able to find as many pairs of matching displacement vectors as there are points in each time interval, then we have found an interpretation that agrees with the premise of straight-line, constant-speed motion for every object. Then again, it is possible that there are several such interpretations. We should therefore store the speeds we have calculated for the present interpretation, keeping them as potential return values, and backtrack to search for other interpretations. What we are doing, in sum, is a depth-first recursion through all possible matchings of displacement vectors. A Java implementation follows.

int n, ct = 0, speeds[], x1[], y1[], x2[], y2[], x3[], y3[], ret[];
boolean used1[], used2[];

void doit(int pos) {
   if (pos == n) {
      ct++;
      for (int i = 0; i < n; i++)
         ret[i] = speeds[i];
      return;
   }
   int i, j, dx, dy, speed;
   for (i = 0; i < n; i++) {
      if (used1[i])
         continue;
      dx = x2[i]-x1[pos];
      dy = y2[i]-y1[pos];
      speed = (int) Math.round(Math.sqrt(dx*dx+dy*dy));
      used1[i] = true;
      for (j = 0; j < n; j++)
         if (!used2[j] && x3[j]-x2[i] == dx && y3[j]-y2[i] == dy) {
            used2[j] = true;
            speeds[pos] = speed;
            doit(pos+1);
            used2[j] = false;
         }
      used1[i] = false;
   }
}

public int[] deduceSpeeds(int[] x1, int[] y1, int[] x2, int[] y2, int[] x3, int[] y3) {
   this.x1 = x1; this.y1 = y1;
   this.x2 = x2; this.y2 = y2;
   this.x3 = x3; this.y3 = y3;
   n = x1.length;
   speeds = new int[n];
   ret = new int[n];
   used1 = new boolean[n];
   used2 = new boolean[n];
   for (int i = 0; i < n; i++)
      used1[i] = used2[i] = false;
   doit(0);
   if (ct == 1)
      return ret;
   return new int[0];
}

Much of this code is devoted to setting up global variables. Note that speeds is used to store a partial result, while ret stores a full result to be returned if it turns out to be the only one. Each time a full matching is found, we increment the counter ct and copy the contents of speeds into ret.

The arrays vital to carrying out the recursive search are used1 and used2. Observe that in each one, the boolean value at the appropriate index is set to true before making a recursive call, then reset to false afterward. They record our tentative decisions as we continue to search through the space of all matchings, so that we don't allocate the same points to different vectors. They serve, in effect, to lock pairs of displacement vectors on a temporary basis during our search for a full interpretation. Understand this, and you understand all.

Value	500
Submission Rate	122 / 176 (69.32%)
Success Rate	107 / 122 (87.70%)
High Score	Eryx for 482.19 points (5 mins 30 secs)
Average Score	349.54 (for 107 correct submissions)

This problem concerns a grille superimposed on a square of text with each cell covering one character. The grille has had one quarter of its cells punched out to form a pattern of holes such that after three 90-degree rotations of the grille, every character will have appeared through a hole exactly once. Given a partial grille, we are to complete it if possible, punching new holes as necessary in the upper-left quadrant.

Consider a cell at some location in the upper-left quadrant of the grille. To what three locations besides this one can it be rotated? In a complete and valid coding grille, there must be a hole at exactly one of the four total possible locations. If, upon inspection, we find that more than one of the four cells has been punched out, the grille is invalid. If they are all intact, we punch out only the one in the upper-left quadrant.

The crux of the matter, then, is to determine how the coordinates of a hole change when the grille undergoes a 90-degree rotation.

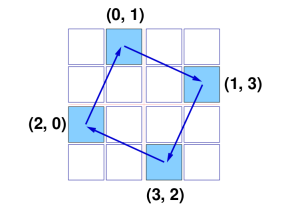
We can determine by trial and error that in an n-by-n grid, a cell at location (i,j) is rotated to (j,n-1-i).

def square(grille):
   n = len(grille)
   for i in range(n/2):
      for j in range(n/2):
         ct = 0
         ii = i
         jj = j
         for k in range(4):
            if (grille[ii][jj] == '.'):
               ct = ct+1
            tt = ii
            ii = jj
            jj = n-1-tt
         if (ct > 1):
            return []
         if (ct == 0):
            grille[i] = grille[i][:j]+"."+grille[i][j+1:]
   return grille

In languages where strings are immutable, the contents of grille cannot be directly altered one cell at a time. Instead, an entire row must be written over with a new string that incorporates slices of the old one.

Value	1000
Submission Rate	18 / 176 (10.23%)
Success Rate	9 / 18 (50.00%)
High Score	tjq for 556.78 points (31 mins 10 secs)
Average Score	463.66 (for 9 correct submissions)

Given the latitude, longitude, and altitude of some satellites and rockets, we are asked to determine which rockets are visible to at least three satellites. Since the line of sight between a satellite and a rocket can be occluded only by the Earth, the problem boils down to deciding whether a line segment intersects with a sphere. Conscientious coders who, unlike me, always paid attention in math class and know their way around a cross product should be able to solve this problem by applying the right formulas. Those of us who aren't equipped with a sophisticated mathematical toolkit need not despair, for we can make do with a bit of visual imagination and a smattering of trigonometry.

The first item on the agenda is to transform the input into a more useful form. Once the location of each rocket and satellite has been rendered in Cartesian coordinates, we'll be able to calculate distances using the familiar Pythagorean Theorem. The diagram below shows a sphere of radius r tilted slightly down and to the right. The equator and latitude zero are drawn in pink. To the west of latitude zero and north of the equator is a blue dot lying on the surface of the sphere at latitude a and longitude b.

Imagine that the center of the sphere is at the origin of a coordinate system whose x axis runs through the equator at the 90-degree longitude, while the y axis runs through the northern pole. The z axis runs through the equator at zero longitude, projecting out of the computer screen and toward your mouse (if you're right-handed).

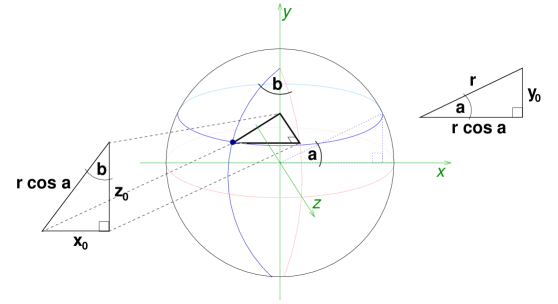
Notice how altitude a defines a plane that cuts through the y axis at the y coordinate of the blue dot. The equator, or latitude zero, lies in the plane where y is always zero. To find the distance between these parallel planes, we examine the right triangle formed by projecting a radius at angle a onto the y=0 plane. This triangle is shown at the right of the diagram. Opposite the angle of measure a is a leg of length rsina, giving the y coordinate of our dot.

The other leg, having length rcosa, spans the distance between the y axis and the surface of the sphere at latitude a. This is also the measure of the hypotenuse of an interesting right triangle. Observe that longitude zero lies in the plane where x is always zero. If we draw the shortest line from the blue dot to this plane, its length is the x coordinate of the dot. Similarly, the z coordinate is equal to the length of the shortest line from the dot to the plane where z=0. These two lines are perpendicular and lie in the plane of altitude a. By sliding the z-coordinate line toward the east, we form a right triangle, as pictured to the left of the sphere. For the purpose of illustration, it has been tilted forward into the plane of the computer screen.

The degree of longitude of the dot, namely b, gives us an acute angle of the triangle. We already know that the length of the hypotenuse is rcosa. Thus, from the basic trigonometric relations, we deduce that the x coordinate is rcosasinb and the z coordinate is rcosacosb. What if we are interested in the Cartesian coordinates of a point lying not on the surface of the sphere, but at a positive altitude? Then we imagine a larger sphere such that the point in question does lie on its surface. The same conversion formulas apply, only with a different r value.

Now that we possess the mojo to calculate Cartesian coordinates for the point corresponding to every satellite and rocket, let's see what we can do with these points. Consider the line segment stretching between a satellite and a rocket. On it is one point that lies closer than any other to the center of the earth. If and only if this point is below the surface of the earth, there is no line of sight between the rocket and the satellite. If we had some way to calculate the distance between the center of the earth and this point, we could compare it with the radius of the earth to make our decision. Bear in mind that we are modeling the earth as a sphere centered at the origin of the coordinate system.

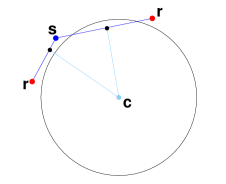
The heavy-duty geometric approach is to draw a line through the satellite and rocket, compute its distance from the origin, and then check for cases where the closest point on the line falls outside the line segment. But the 3D line-point distance calculation is somewhat esoteric, and anyway there is no need for exact methods when a problem calls for absolute precision of 1e-6. There happens to be a concise numerical method that does not concern itself with any special case.

Let the center of the earth be the apex of a triangle whose base is the line segment between the rocket and the satellite. In searching for the point on the triangle base nearest the origin, let us suppose that the rocket is farther than the satellite from the origin. It is then useful to see that the midpoint of the base is closer than the rocket to the origin, but still far enough that the closest point lies between it and the satellite. We can therefore restrict our search to that half of the base lying between the midpoint and the satellite. The diagram below shows why this is true.

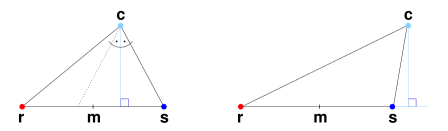
If the height of the triangle is incident on its base, then the midpoint must fall between the height and the rocket, or else the rocket wouldn't be farther than the satellite. Observe that the height bisects a smaller triangle formed by horizontally reflecting the leg that ends in the satellite. If, on the other hand, the height falls outside the base, then the closest point to the apex is in fact the satellite, so it can't hurt to halve the distance to it.

The converse arguments apply if it is not the satellite but the rocket that lies nearer the origin. In either case, we can construct a triangle with the same apex and the same height as the original but with a base only half as wide, having the pleasing property that it includes the closest point to the apex. We can carry out further iterations of the procedure, always choosing that half of the base lying between the midpoint and the shorter leg, until we are arbitrarily close to the true answer.

Once we have computed the distance between the origin and every line segment formed by a satellite and a rocket, we know which rockets are visible to which satellites, and it remains only to tally the number of satellites per rocket. Below are the essential parts of a Java implementation, starting with a function that converts from spherical to Cartesian coordinates.

double[] sph2car(double altitude, double latitude, double longitude) {
   double[] ret = new double[3];
   ret[0] = altitude * Math.cos(latitude) * Math.sin(longitude);
   ret[1] = altitude * Math.sin(latitude);
   ret[2] = altitude * Math.cos(latitude) * Math.cos(longitude);
   return ret;
}

We shall make use of a utility function that copies one 3D coordinate to another.

void p2p(double[] pFrom, double[] pTo) {
   for (int i = 0; i < 3; i++)
      pTo[i] = pFrom[i];
}

In the following loop, rocs and sats are the arrays in which we have stored the Cartesian coordinates of the rockets and satellites, respectively.

for (int i = 0; i < rocs.length; i++) {
   for (int j = 0; j < sats.length; j++) {
      double r[] = new double[3], s[] = new double[3];
      double dr, ds;
      p2p(rocs[i], r);
      p2p(sats[j], s);
      while (true) {
         dr = Math.sqrt(r[0]*r[0]+r[1]*r[1]+r[2]*r[2]);
         ds = Math.sqrt(s[0]*s[0]+s[1]*s[1]+s[2]*s[2]);
         if (Math.abs(dr-ds) < 1e-6)
            break;
         double[] m = {(r[0]+s[0])/2, (r[1]+s[1])/2, (r[2]+s[2])/2};
         if (dr > ds)
            p2p(m, r);
         else
            p2p(m, s);
      }
      dist[i][j] = dr;
   }
}

Thus, having made use of little specialized knowledge but much insight, we tame a three-dimensional geometry problem with a humble binary search.