
|
Match Editorial |
Tuesday, November 25, 2003
Match summary
SRM 173 had no big surprises, with many of the usual names in the top. SnapDragon proved fastest on the first two problems and WishingBone on the last, but still the winner was ZorbaTHut despite no challenges. Notably for a problem set that I write was that 5 people managed to solve the hard problem!
Divison two was mainly a battle between blackbeltcoder4 and newcomer avenger, where in the end blackbeltcoder4 got the best overall score.
The Problems
ProgressBar
Used as: Division Two - Level One:
Value 250 Submission Rate 253 / 267 (94.76%) Success Rate 231 / 253 (91.30%) High Score dRaa for 248.38 points (2 mins 17 secs) Average Score 200.22 (for 231 correct submissions)
First we calculate how long time the installation has been running by summing up the execution times of the finished tasks (call this elapsedTime), and then sum up all the times to get the totalTime. Obviously, the amount (in percentage) that has been completed is elapsedTime/totalTime. One could calculate this percentage, using float or double, multiply with 20 and round down using the floor function (or simply cast it to an int). However, since we're dealing with integers only, it's nicer to use integer math completely. One should know that integer division always round down. So we can calculate 20*elapsedTime/totalTime using integer math to directly get the number of '#' characters to use in the resulting string. To create the string, start with an empty string and use two for-loops: one to fill the '#' characters and one to pad this with '.' characters until the total length is 20. Shortcuts may be possible, using the languages built-in functions for string creation.
WordForm
Used as: Division Two - Level Two:
Used as: Division One - Level One:
Value 500 Submission Rate 212 / 267 (79.40%) Success Rate 169 / 212 (79.72%) High Score dRaa for 486.65 points (4 mins 43 secs) Average Score 344.68 (for 169 correct submissions)
Value 250 Submission Rate 191 / 193 (98.96%) Success Rate 178 / 191 (93.19%) High Score SnapDragon for 247.20 points (3 mins 1 secs) Average Score 215.23 (for 178 correct submissions)
This task can be broken into two sub task: The first task is to deduce for each letter if it's a vowel or a consonant while the second is to put together the return string.
This check is trivial for all letters except 'Y' (it's probably convenient to first convert the letter to uppercase using toupper or similar). Deducing whether 'Y' is a vowel or a consonant requires that we know if the previous letter was a vowel or a consonant. Therefore it makes sense to check the letters from left to right, so when we reach a 'Y' we already know if the previous letter was a consonant or a vowel. This might sound trivial, but is actually an (easy) example of dynamic programming, something I know many TopCoders have problems with. The base case is of course the first letter, then by definition 'Y' should be considered a consonant. The 'C' and 'V' characters can either be appened to a new string, or be stored in the input string by simply replacing the original character.
In the second task we start with an empty result string and then loop over all characters from left to right in the string with 'V' and 'C'. A character from the latter string is appened to the end of the result string if it's different from the last character added, or if the result string is empty. These two steps can of course be done simultaneously: Once we've figured out if a letter is a 'V' or a 'C', we check if the last added letter to the return string is the same. If not, we append the new character, otherwise it's ignored.
Centipede
Used as: Division Two - Level Three:
Value 1000 Submission Rate 27 / 267 (10.11%) Success Rate 6 / 27 (22.22%) High Score blackbeltcoder4 for 532.53 points (33 mins 38 secs) Average Score 460.04 (for 6 correct submissions)
I've never played the original Centipede, and I am sure the description of the centipedes movement in the problem description differs from the original. I apologize for that...
I start this solution description by describing how the actual simulation of the centipedes movement can be implemented, and then show how to make it fast enough to work on large inputs (i.e. when we have to simulate more than, say, 100 million time units).
The centipede is easiest represented by an array containing 10 points (or two int arrays, one with the x-coordinates and one with the y-coordinates), one point for each segment. I will let index 0 in this array be the head and index 9 be the last part of the tail. We also need to know the horizontal direction of the centipede, which is either 1 or -1.
Initially the head is located at 10,0 and the last part of the tail at 1,0 (0,0 being the top left corner, which will always be an obstacle) and the remaining segments in between, since we're guaranteed that all these squares in will be empty. The horizontal direction should be set to 1.
We will need a function to move the centipede, given the new position of the head and direction. This function should shift all elements in the centipede array and update the head location as well as the direction. One could use a faster data structure (like a circular list) to avoid shifting all elements, but this is really not necessary when the array only contains 10 elements.
To simulate a time unit, we start by checking if the centipede can move in its current direction, that is, if the position where the head will be if it's moved in the current horizontal direction is empty. If so, use the move function defined in the previous paragraph. Otherwise we check if the square directly below the head is empty. If so, use the same move function to move the centipede down, and also change the horizontal direction. Otherwise we call the same function, but make sure to only change the direction. It's critical that we call the move function here even though the head doesn't change position, but the remaining part of the centipede will! The pseudocode for this simulation is thus as follows:
if square_empty(centipede[0].x + centipede_dir,centipede[0].y)
update_centipede(centipede[0].x + centipede_dir, centipede[0].y, centipede_dir)
else if square_empty(centipede[0].x, centipede[0].y + 1, -centipede_dir)
update_centipede(centipede[0].x, centipede[0].y + 1, -centipede_dir)
else
update_centipede(centipede[0].x, centipede[0].y, -centipede_dir)
There is one minor complication: what should we do when the centipede starts to move out at the bottom of the screen? The easiest solution is to let the function called square_empty above return true for all positions below the screen. This will make the centipede move horizontally below the screen, but that's ok. Just make sure that you don't do any array indexing using the x-coordinate, because it might very well be negative (since there are no obstacles at all on that row)!
After the if-statements above, one thing remains, namely to check if the centipede has completed a cycle. It has done so when the last part of the tail has just left the screen, i.e. when centipede[9].y is outside the screen. At this instant, immediately reset the centipede at the top of the screen, preferably using the same routine as when initializing the centipede at the beginning of the simulation. Make sure you don't get any off-by-one errors here, like being a time unit too early or too late.
Finally, when all time units have been simulated, just loop through all segments and mark them (if they're visible) in the screen layout.
So, that was a very detailed description of the simulation. It should come as no surprise that you have to do slightly more than this to get the solution working though, since the statement warns for large inputs, and the last example case also demonstrates this. What one has to do here is realize that every time the centipede restarts (i.e. every cycle), it will take the exact same path again and again. It's thus pretty pointless to simulate this path over and over again. Instead we could simulate exactly one cycle, and find out how long time this takes, i.e. the cycle length (note that the centipede will always complete a cycle given enough time due to the input constraints). We then take the given amount of time units modulo the cycle length (that is, the remainder of the divison <time units>/<cycle length>) and will then end up with the number of time units we need to simulate the centipede in it's last cycle.
We can use the simulation algorithm above to both find the cycle length and simulate the last cycle, or even do both tasks at once, doing the modulo calculation when the centipede is about to start its second cycle. Doing both tasks at once is slightly more error prone though, which I found out when I first wrote my solution...
TreasureHunt
Used as: Division One - Level Two:
Value 500 Submission Rate 146 / 193 (75.65%) Success Rate 77 / 146 (52.74%) High Score SnapDragon for 466.25 points (7 mins 45 secs) Average Score 289.09 (for 77 correct submissions)
It surprised me that so many failed this problem. I suspect the reason was failing to understand the details in the problem (maybe reading the problem statement too fast). Or maybe it was just a poor wording from my part? The problem survey will probably tell...
Once you understand the task, it's pretty straightforward. It can essential be described like this in pseudocode:
Find the location of the X on the map
Loop through all valid starting points:
Walk according to the instructions
If we didn't walk on any water squares:
Did we end up on a square which is closer to the X?
(or same distance and better tiebreaker)
If so, update best position found
A starting point is valid if it's a beach, which are precisely those squares that:
- Is a land square ('O' or 'X') and
- Lies on the border of the map (since all squares outside the map are water) or
- Is adjacent to a '.' square on the map
To take care of the last two tiebreakers, we just have to loop over all points in row major order (that is, y-coordinate in the outer loop, and x-coordinate in the inner). If we only update the best starting location when a shorter distance has been found, this will work because the order of the loops guarantee that we find the wanted location in case of several treasure locations at the same distance. Note that we loop the start location but that's it's the treasure location we should do these tiebreakers on. However, when it comes to smallest x- & y-coordinate, this doesn't matter as the treasure location is just a translocation of the start location.
ElectronicScarecrows
Used as: Division One - Level Three:
Value 1000 Submission Rate 26 / 193 (13.47%) Success Rate 5 / 26 (19.23%) High Score WishingBone for 666.26 points (22 mins 38 secs) Average Score 535.57 (for 5 correct submissions)
Ignoring the story and concentrating on the underlying problem, one quickly realizes it can be formulate like this: Given a set of points P, find a subset S of these so that |S| <= k and that the area of the convex hull of S is maximized.
It's tempting to begin to find the convex hull of P and then work from there, but this turns out not to be necessary. Of course, for those who have prewritten convex hull code lying around, it doesn't hurt either, especially since having a convex hull might make the rest of the solution seem easier. I won't explain how to find the convex hull from a set of points as this is one of the first computational geometry algorithms taught, and there are plenty of resources on the web - just search for "convex hull" and "graham's scan" on Google.
It should maybe be noted that a point p that is not in the convex hull can not be part of an optimal solution because then another point q in the convex hull would exist so that replacing the p with q would create a new polygon which contains the whole old polygon; again, I won't explain this further since as I said, there's no need to calculate the convex hull.
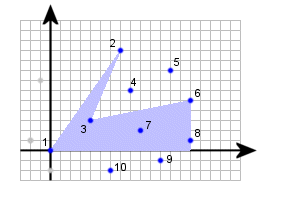
There are many ways to solve this problem, but the "easiest" of them (which also is the slowest probably) works like this:
First select a starting point (loop over all points in P) and call this one Q1. In the picture to the right, this point is marked with 1. Create a new set Q of points where Q1 is the origin. All points strictly to the left or with the same x-coordinate and below of Q1 are not included in Q (for instance, if the gray points in the figure exist in P, they should not exist in Q). Now sort the points in Q according to their angle. If several points have the same angle (like point 3 and 4 to the right), select the one closest to Q1 first. We then get an ordered list of points, and the numbers next to the points in the figure shows this ordering in this particular case.
The idea is now that if we create a polygon starting at Q1 and then select points with increasing numbers (and end with Q1), we will always end up with a simple polygon (a simple polygon is one where the edges don't intersect). As stated in the problem description, the area formula for the polygon only works properly if the polygon is simple. Also, all convex polygons that we can create from these points can be found this way, so we won't miss the polygon with the maximum area.
The next step requires that you understand how the polygon area formula works. When going betweeen two points, say Q1 and Q2, we calculate the area below this edge. The formula for this is, as you should have learned in high school, (x2 - x1)(y2 + y1) / 2 = (x2y2 + x2y1 - x1y2 - x1y1) / 2. (However, the two terms xkyk will both be canceled out when going from Qk to the next (or previous) point, which is why we only have to care about (x2y1-x1y2) / 2, and doing this over all edges gives us the polygon area formula.)
If we look at the original formula (x2 - x1)(y2 + y1) / 2 we see that if we go from left to right (x2 > x1), the area increases, but when going left, it decreases (asssuming we're above the x-axis anyway, otherwise everything will be inversed). Now look at the picture. Here we have started to select a polygon, choosing the points Q1, Q2, Q3 and Q6. The area in blue is the current area of the polygon that we have added. If the next point would be, say, Q7, we would remove the area below the edge between Q6 and Q7 since we're going from right to left.
So how do we find the largest area we can create? We can visualize this problem as a graph problem actually, where each node in the graph correspond to a point in Q, and let the edges in the graph correspond to selecting an edge in the polygon. The weight of each edge is of course the area that walking this edge would add (or decrease) from the polygon area. Since all edges are from a node with a lower index to a node with a higher index, we have what is called a direct acyclic graph (DAG). Since we have to "close" the polygon, it might be convenient to create a copy of Q1 and let it be the last vertex (with no outgoing edges). What we want to do now is to find the longest path, starting at Q1 and ending at the duplicated Q1 node, traversing exactly k edges. Such a path will correspond to selecting the polygon with the largest area, since the length of the path is the area of the selected polygon.
Finding this path can be done using dynamic programming. If we define the function longest_path like this:
longest_path(current_node, selected_nodes) =
set max_area= 0
loop through all nodes x greater than current_node
if longest_path(x,selected_nodes+1) + area_below(current_node,x) > max_area
update max_area
return max_area
the largest polygon has the area longest_path(1,0).
This is a mathematical function without side effects, so the size of the input domain is kn, where k = number of nodes to select and n = number of nodes in Q. Thus we only have to compute it kn times, and evaluating it once requires at most looping through n nodes. Since we already have an outer loop checking all start points, the overall complexity of this algorithm becomes O(k n3). There are several ways to optimize this algorithm, but doing so in a SRM is not necessary and only a waste of time. I'll leave them to the reader as an exercise...
It turns out that the fastest algorithms is very much faster than this. The best I've found has a worst case complexity O(kn + nlog n). An implementation of this algorithm can be found in the huge computational geometry library CGAL, http://www.cgal.org. The function is called maximum_area_inscribed_k_gon_2 and requires that you first compute the convex hull of P.
