
|
Match Editorial |
Tuesday, June 17, 2003
Match summary
The two matches prior to SRM 151 saw very few submissions on both the division one medium and hard problems, but this time the coders in both divisions submitted merrily. In division one, newcomers aneubeck (2nd place) and tomek (4th place) pushed hard, but it was for the "oldster" radeye to take the top spot. It is notable that bilingual tomek submitted in both C++ and Java, an event rarely seen with the top finishers. noah won division two finishing only 9 points ahead of JWizard. First timer m00tz finished third and was the only first timer to hit the yellow rating category.
The Problems
PrefixCode
Used as: Division-II - Level 1:
Value 250 Submission Rate 177 / 213 (83.10%) Success Rate 109 / 177 (61.58%) High Score farsight for 248.08 points
Surprisingly many submissions on this problem failed, mainly because not the lowest index of a prefix was returned, but any index of a word
that had a prefix.
Simply consider the words in the given order and for each word, check if it is the prefix of another word.
Java
public String isOne(String[] words)
{
for (int i=0; i<words.length; i++)
for (int j=0; j<words.length; j++)
if (i != j && words[j].startsWith(words[i]))
return "No, " + i;
return "Yes";
}
Birthday

Used as: Division-II - Level 2:
Value 500 Submission Rate 161 / 213 (75.59%) Success Rate 73 / 161 (45.34%) High Score Ceranith for 486.64 points
There are several possibilities for solving this one.
One of the possibilities is the following:
Extract the day and the month from the current date and from all birthdays.
In a loop, first check if the current day coincides with any of the
birthdays. If so, return that day. If not, set the current date to
the following day (paying attention to the start of a new month/year).
The shorter and less error-prone solution is to sort the birthdays, unmodified, as strings (in ascending order). Go through the sorted birthdays until the first birthday
that occurs on or after the current date is found and return it. If no such
birthday is found, all given birthdays occur before the current date (looking
at a fixed year), so return the first birthday in the sorted list, which
is the first birthday occurring when a new year begins.
C++
string getNext(string date, vector<string> birthdays)
{
sort(birthdays.begin(), birthdays.end());
for (int i=0; i<(int)birthdays.size(); i++)
if (birthdays[i].substr(0, 5) >= date)
return birthdays[i].substr(0, 5);
return birthdays[0].substr(0, 5);
}
MergeSort

Used as: Division-II - Level 3:
Used as: Division-I - Level 2:
Value 1000 Submission Rate 75/ 213 (35.21%) Success Rate 45 / 75 (60.00%) High Score m00tz for 893.29 points
Value 500 Submission Rate 140 / 145 (96.55%) Success Rate 109 / 140 (77.86%) High Score Yarin for 481.98 points
Implement the MergeSort algorithm as described, run it on the input, and count the number of comparisons made.
C++
int howManyComparisons(vector<int> a)
{
return mergeSort(a);
}
int mergeSort(vector<int>& a)
{
if (a.size() <= 1)
return 0;
int k = a.size() / 2;
vector<int> b = vector<int>(a.begin(), a.begin()+k);
vector<int> c = vector<int>(a.begin()+k, a.end());
int cb = mergeSort(b);
int cc = mergeSort(c);
return cb + cc + merge(a, b, c);
}
int merge(vector<int>& a, vector<int>& b, vector<int>& c)
{
unsigned ai = 0, bi = 0, ci = 0, comps = 0;
while (bi != b.size() && ci != c.size() && ++comps)
if (b[bi] == c[ci])
{
a[ai++] = b[bi++];
a[ai++] = c[ci++];
}
else
if (b[bi] < c[ci])
a[ai++] = b[bi++];
else
a[ai++] = c[ci++];
while (bi != b.size())
a[ai++] = b[bi++];
while (ci != c.size())
a[ai++] = c[ci++];
return comps;
}
Archimedes

Used as: Division-I - Level 1:
Value 250 Submission Rate 129 / 145 (88.97%) Success Rate 122 / 129 (94.57%) High Score antimatter for 248.78 points
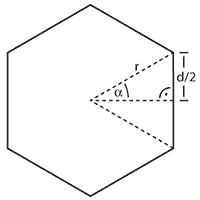 The solution to this problem may be the shortest a TopCoder problem has ever seen.
However, there is some basic geometry to be done before the return statement can be written.
The solution to this problem may be the shortest a TopCoder problem has ever seen.
However, there is some basic geometry to be done before the return statement can be written.
Taking the perimeter of a n-sided regular polygon
To calculate the length of a side from the polygon, take a look at the image on the left:
For the little right triangle we get
Java
public double approximatePi(int numSides)
{
return numSides * Math.sin(Math.PI / numSides);
}
Gauss

Used as: Division-I - Level 3:
Value 1000 Submission Rate 72 / 145 (49.66%) Success Rate 43 / 72 (59.72%) High Score radeye for 939.97 points
What came to my mind first is the following
(it is too slow on the given constraints, but the technique
may be useful for other problems):
Start with lower = 1, upper = 1 and sum = 1 (sum is
supposed to be the sum of all numbers from lower to upper). Do a loop
while upper <= target/2 + 1:
If sum equals target, add [lower, upper] to the solution.
If sum <= target expand the interval (upper++ and sum += upper),
and if sum > target shorten the interval (sum -= lower and lower++).
This way all intervals can be found but the running time is
linear in target, which is too much since target can be as high as
100.000.000.000.
First, observe that the maximum number of numbers added to get target occurs
in the case where adding starts from 1. Assume that target is the sum of the
numbers from 1 to n for some n:
So target can potentially be the sum of anywhere from 2 to n consecutive numbers. A single check as to whether target is
the sum of m numbers (2 <= m <= n) can be done in constant time, also yielding the numbers to be added.
Consider the cases where m is odd and m is even for an example, n = 30:
n = 30 m = 5 4 5 6 7 8 n / m = 6 n % m = 0
n = 30 m = 4 6 7 8 9 n / m = 7.5 n % m = m/2
If m is odd and n/m is integral, n/m is the number in the middle of the numbers that add up to target.
If n/m is not integral, there is no solution for m. (Informally, n/m is the 'average weight' of the numbers
that need to be added; take n/m and (m-1)/2 numbers to the left
and to the right of n/m, respectively.)If m is even, n/m must be x.5 for a solution to exist (for some integer x). The solution is the next m/2 integral numbers less than and greater than n/m, respectively. (Again informally, n/m is the 'average weight' of the numbers that need to be added, and if n/m = x.5 each 'pair' of numbers from the left and the right of n/m has this average weight.) The complexity is O(sqrt(target)).
Java
public String[] whichSums(String target)
{
java.util.Vector v = new java.util.Vector();
long t = Long.parseLong(target);
int n = (int)(Math.sqrt(0.25+2*t) - 0.5);
for (int i=n; i>=2; i--)
{
if (i % 2 == 1 && t % i == 0)
v.add("[" + (t/i-i/2) + ", " + (t/i+i/2) + "]");
if (i % 2 == 0 && t % i == i/2)
v.add("[" + (t/i-i/2+1) + ", " + (t/i+i/2) + "]");
}
return (String[])v.toArray(new String[0]);
}
The number of ways to represent n as the sum of consecutive positive numbers is equal to the number of odd divisors of n. Try to prove it yourself or take a look at the proof at the end of this old newsgroup post and read more at the On-Line Encyclopedia of Integer Sequences.
