
|
Match Editorial |
Wednesday, March 26, 2003
The Problems
SoccerLeague
Used as: Division-II, Level 1:
Value 200 Submission Rate 186 / 195 (95.38%) Success Rate 180 / 186 (96.77%) High Score aastor for 199.54 points
Reference implementation: Yarin (practice room)
Implementation
This problem is unusually easy, even for a Division-II Level 1 problem. We can initialize the maximum points value to 0, as no team will have negative points. We then loop through all teams, and for each team check how many points they've been awarded by the simple formula 3*wins+1*ties. If this is greater than the maximum value found so far, we update the maximum value with this new value.
SpriteCollision
Used as: Division-II, Level 2:
Used as: Division-I, Level 1:
Value 600 Submission Rate 127 / 195 (65.13%) Success Rate 78 / 127 (61.42%) High Score Sleeve for 557.81 points
Value 300 Submission Rate 130 / 134 (97.01%) Success Rate 108 / 130 (83.08%) High Score sjelkjd for 295.00 points
Reference implementation: Yarin (practice room)
Implementation
One can solve this problem using at least three different methods. In the first two of these, we check for every pair of sprites (two nested loops, make sure not to check a sprite against itself!) whether they collide or not. This check consist of finding out whether or not two rectangles overlap; that is, if they intersect. This can be done either using Javas geometry library (method 1), or by the following reasoning: if two rectangles A and B do not overlap, then either
- The right side of rectangle A is to the left (or the same) of the left side of rectangle B
- The left side of rectangle A is to the right (or the same) of the right side of rectangle B
- The upper side of rectangle A is below (or the same) the lower side of rectangle B
- The lower side of rectangle A is above (or the same) the upper side of rectangle B
In all other cases, the two rectangles overlap (method 2).
The third method is to actually plot the sprites on a virtual screen. This is feasible since the screen size is so small, 256x256 pixels. Initially we mark all pixels as empty; that is, no sprite occupies this pixel. Then, for each sprite, we use two nested loops to mark all pixels this sprite occupies. If, when doing this, we intend to mark a pixel that has already been marked, then obviously two sprites collide. These two sprites are the one already marked (when marking, we store the sprite index of the sprite) plus the one we are currently marking. We need to add both to a list of sprites marked as "collided". We then continue the process until all sprites have been plotted. Finally we return a sorted array of the sprites marked as collided (also making sure no elements are duplicated).
DrawCircle
Used as: Division-II, Level 3:
Value 1000 Submission Rate 59 / 195 (30.26%) Success Rate 33 / 59 (55.93%) High Score vegeta for 932.57 points
Reference implementation: Yarin (practice room)
Implementation
Consider the image below, where a coordinate system has been inserted. Each pixel in the bitmap (from here on, I will use the term square instead of pixel) has length 1 in this coordinate system.
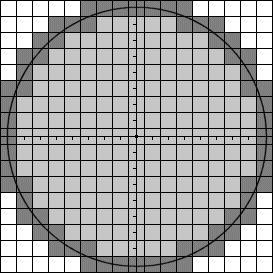
To determine if a square is entirely inside the circle, we would like to check the distance from all points in the square to the centre of the circle. If all those distances are less than the radius, then the whole square is inside the circle and thus this we know this square should be represented by a 'x'. We can apply the same reasoning to decide if a square is entirely outside the circle, a '.'. If it's neither entirely inside nor outside the circle, it's obviously on the edge, a '#'.
Now, the trick is that we don't actually have to check all points (there are of course infinitely many points inside the square) - it's enough to just check the distance from the four corners of the square to the centre of the circle. The coordinates for the corners of square x,y (0,0 being the square where the centre of the circle is located in) is (-0.5+x,-0.5+y),(0.5+x,0.5+y),(-0.5+x,-0.5+y),(0.5+x,0.5+y). The distance from a point to the centre is calculated using Pythagoras formula, a2+b2=c2.
// Return TRUE if square x,y (0,0 = centre square) is entirely inside the circle
boolean isInside(int x, int y, int radius)
{
double cx,cy;
cx=-0.5+x; cy=-0.5+y; // Upper left corner
if (cx*cx+cy*cy>radius*radius) return false;
cx= 0.5+x; cy=-0.5+y; // Upper right corner
if (cx*cx+cy*cy>radius*radius) return false;
cx=-0.5+x; cy= 0.5+y; // Lower left corner
if (cx*cx+cy*cy>radius*radius) return false;
cx= 0.5+x; cy= 0.5+y; // Lower right corner
if (cx*cx+cy*cy>radius*radius) return false;
return true;
}
Similar code is used for the function isOutside. When those are written, we loop through all squares, from -radius to radius (inclusive) in both horizontal and vertical direction and check what kind of square this is.
One can avoid using floating point math if the whole coordinate system is scaled up by a factor of two. I prefer this method because, if it's possible, one should always avoid using floating point (double). In this problem it's not necessary at all, because the problem statement guaranteed that the circle never touched the corners precisely, in which case floating point math must be used with care.
This problem can also be solved with the help of Javas geometry library, using intersections of circles and rectangles.
RoundRobin
Used as: Division-I, Level 2:
Value 500 Submission Rate 87 / 134 (64.93%) Success Rate 71 / 87 (81.61%) High Score SnapDragon for 466.06 points
Reference implementation: Yarin (practice room)
Implementation
A trick which makes solving this problem easier is to realize that you should consider all points from 0 to 2*n, inclusive, as point groups. Most likely most of these will contain no players at all, but that won't affect the outcome of the sorting.
Obviously, we need to start calculating the total score for each player so we know which point group the player belongs to. Once that's done, for each player i we create an array - call it v - where the v[j] is the score player i took against all players in point group j and above. If we use the trick in mentioned in the previous paragraph, this becomes really easy - v[j] is simply the score player i took against all players whose score is greater (or equal) to j. A couple of nested loops through all players and points is the only thing required to calculate the v array for each player.
Now we can sort. When comparing two players, we first check element 0 in each players v'array (this is the same as the total score of the player). If it's the same, check the next element etc. If it's the same for all elements, we check the player index. The easy way to do that is to add an extra element to the array v, containing the player index.
In C++, the code becomes extremely short because there's a default less-than operator for vector which does what we want:
vector<int> order(vector<string> r) {
vector< vector<int> > v;
vector<int> sc(r.size(),0);
for(int i=0;i<r.size();i++) for(int j=0;j<r.size();j++)
sc[i]+=isdigit(r[i][j])?r[i][j]-'0':0;
for(int i=0;i<r.size();i++) {
// 98 points is max due to the problem constraints
vector<int> t(100,0);
// Element 0-98 are for point group results, element 99 = player index
t[99]=i;
for(int j=0;j<99;j++) for(int k=0;k<r.size();k++)
if (sc[k]>=j) t[j]-=isdigit(r[i][k])?r[i][k]-'0':0;
v.push_back(t);
}
sort(v.begin(),v.end());
// Fetch the player indexes from the sorted vector
for(int i=0;i<r.size();i++) sc[i]=v[i][99];
return sc;
}
Knapsack

Used as: Division-I, Level 3:
Value 1100 Submission Rate 11 / 134 (8.21%) Success Rate 0 / 11 (0.0%)
Reference implementation: Yarin (practice room)
Implementation
Yet again I managed to write a problem which no one solved. Some of the contestants were really close though; for instance a missing type cast from int to long long was the only mistake SnapDragon had in an otherwise flawless solution.
This is an undisguised version of the 0-1 Knapsack problem, a problem mentioned in most algorithm books. This problem is NP complete, meaning that in general it's hard to solve unless the input constraints are "nice". Almost always it's the upper bound for maxWeight that is small enough which lets you loop through all weights and apply dynamic programming. Obviously, this is not the case with this problem, hence it being a Division-1 hard problem.
Since the number of objects is quite small, at most 34, it's tempting to use a brute force algorithm, trying all 2n combinations. 234 is way too much though, but some clever pruning should reduce the number of combinations we have to try a lot. It makes sense to select the most valuable objects first (the objects with the greatest quotient value/weight) since it's more likely on a random input that those objects are in the optimal solution. When pruning, we can estimate if it's possible to surpass the best combination found so far with the objects we haven't yet considered. This solution works very well on randomized inputs. However, a quick look at the last example should tell you that this test data is not random - rather the opposite in fact...
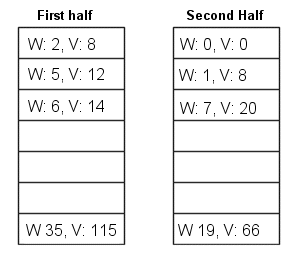
The "correct" way to solve the problem is to use a solution a "split-and-merge" strategy (not quite divide and conquer). We split the objects into two halves of equal size (or if n is odd, nearly equal size). Each half contains at most 17 objects. This is a quite small number, so for each half we can try all 2m combinations of selecting objects. All these combinations (for each half) can now be sorted according to value, weight, number of objects and object set (in that order). We also make sure to remove all bad combinations. A bad combination is something that could never be part of an optimal solution - for instance, having a set of objects that weigh more but has less value than some other set of objects. This filtering can be done in linear time (a single loop through all set of objects) once they have been sorted. Again, we treat each half separately.
Now it's time to merge the two halves (see picture). We start with the combination in the first half which has the highest value (and weight) and in the second half with the lowest value. Then we keep either going up in the left half or down in the right half depending on whether the total weight of the current combination in the left and right half is less than or greater than maxWeight. After every step, we check if the new merging of the combination to the left and combination to the right is better than the best one found so far. This is repeated until we reached the top in the left half or the bottom in the right half. We will then have found the optimal solution.
