May 21, 2018 TCO18 Marathon Round 1 – The Recap
Round 1 of TCO18 Marathon competition was the second round of the qualification to this year finals. The first one being TCO18 Poland Lighting Round. Both of them had variations of classical open problems in Computer Science as their tasks – Steiner Trees and Graph Coloring, respectively. Both tasks were written by Mariia Mykhailova (aka. Nickolas).
These two subjects are well studied in the narrow circle of computer scientists. I will start explaining the RoadsAndJunctions task from selected basics of Graph Theory.
Minimum Spanning Tree
You can to skip to the next section if you know the subject and scored more than 980.000 points provisionally.
Let us simplify the task and forbid to build junctions. Then, all we need to do is to connect N (10 ≤ N ≤ 100) given cities into a tree. From the tree definition it follows that the result tree must have exactly N-1 edges.
There are two most commonly used algorithms for constructing the Minimum Spanning Tree, or MST of a graph. The first, Prim’s algorithm, is also first of the these two historically (but not the first out of all discovered algorithms for MST). The second algorithm we need is Kruskal’s algorithm. Both algorithms are based on the greedy idea.
Please follow the links to follow up if this subject is not familiar to you.
There are some specifics of the given task, however: the graph is complete and can be represented on a 2D Euclidean plane. This means that there are exactly N∙(N-1)/2 edges to select from. Both Prim’s and Kruskal’s algorithms can be adapted to facilitate this and run in O(N^2) time instead of the O(N^2∙log(N)).
The idea for Prim’s algorithm modification is to get rid of the priority queue and instead maintain an array of current distances from the currently built tree to the unvisited vertices. Then, for each vertex V that is added to the tree, update the distance-so-far to all the unvisited vertices, if it can be improved through V.
For Kruskal’s, use the heapify operation, that runs in O(N) time. Even better, it is already there in C++.
Steiner Tree
Now let us increase the difficulty of a task and allow to build the junctions, or additional vertices, while constructing the MST. This task seems to be much harder and does not presently have an exact algorithm with polynomial linear time. The roots of the tasks go to Pierre de Fermat, who raised the question if 3 points on a plane can be interconnected optimally, using 1 extra joint point. The task was generalized to connecting N points on a plane using 1 auxiliary point by Jacob Stiner. It was generalized even more in 20th century to cover cases with multiple auxiliary points.
Despite the Steiner tree problem stays NP-hard, it seems can be solved for relatively small amount of cities. Given N ≤ 100, Przemyslaw Debiak (aka. Psyho) says that it is solvable exactly in less than 10 seconds.
Fermat Point
As mentioned early in this post, Fermat raised the problem of connecting 3 points on a plane optimally, using single auxiliary point. Evangelista Torricelli solved the instance:
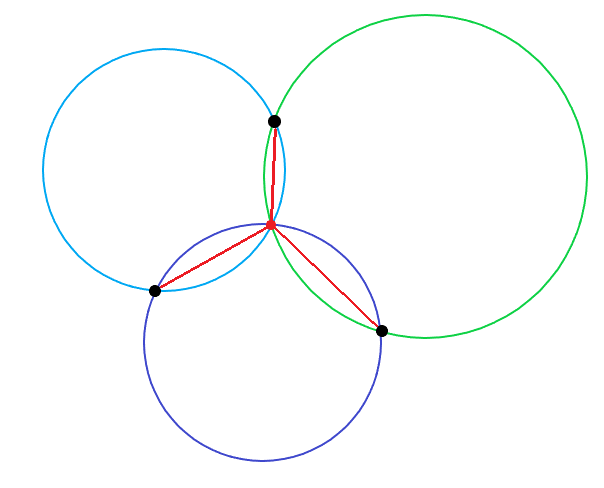
Here, the angles forming by 3 edges going from a red dot – the Fermat point – are 120°.
It was proven later that any Steiner Tree should have all the auxiliary vertices having exactly 3 neighbors, either from original points, or other junctions. Moreover, the Steiner points should also be Fermat points.
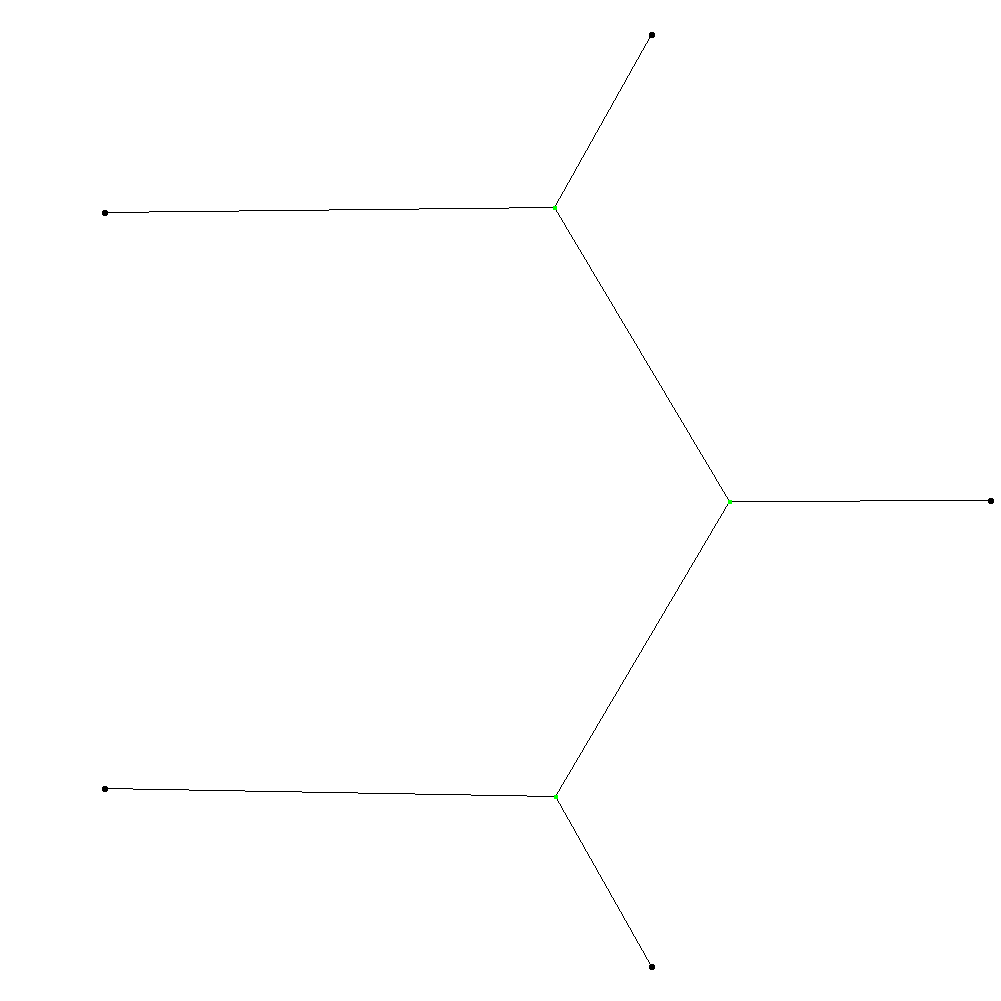
Back To The Task
However, the task says that a junction (Steiner Point) construction may fail. Even worse, you still get charged for the requested junctions, even if they fail. That implies some balance to be found between excessive amount of junctions and too little junctions.
It became clear during the last day to me that the seeds with low cost of junction will perhaps be the determining during the final testing phase. Unfortunately, it was too late and I even did not manage to run the modified tester – with 0.01 cost of junction for each seed – on my latest solution before the submit.
Another thing to note is that the low-cost seeds are more error prone, and I spent some hours during the last day fixing the negative scores on these seeds.
I will give a word to Przemyslaw now:
“<…> GeoSteiner is a state-of-the-art Steiner Tree solver. On their webpage you can find a decent paper with a lot of useful knowledge about the problem.
One way of solving the problem is to generate all possible FSTs (Full Steiner Tree – trees where two terminal nodes are never connected directly) first. In randomly distributed set of points there’s O(N) of them (after pruning).
There are tons of variants for MST algos where you can perform various optimization. Probably the most useful one was so-called Lune property – edge UV can’t be part of the MST if there’s a vertex W that |UW|<|UV| and |VW|<|UV|. This is way faster to implement than Delaunay triangulation and reduces the number of useful edges to O(N). In practice you can precompute this for most of the situations so that doing MST takes nearly O(N) instead of O(N^2 log N). This is especially useful when calculating EV of a particular solution.
When optimizing solution globally, and figuring out if it makes sense to move some points you don’t have to recalculate EV for the whole graph after each move. You can assume your MSTs won’t be affected and just save the number of occurrences for each edge that was used in those MSTs. Then, it takes O(1) to recalculate EV after a single move.
My solution:
- Generate all FSTs of size 3 (Fermat Point) & 4 (Hill Climbing).
- HC on the order of FSTs: Greedily add FST if it improves junction_cost * new_junctions + old_mst * failure_p + new_mst * (1 – failure_p).
- Take the best 40 solutions, calculate EV for all of them and select the best one.
- Perform global HC on a single solution: add redundant junctions & move junctions. <…>”
Lune Property
A lune is a figure that is formed on a plane by two arcs that intersect at two points:
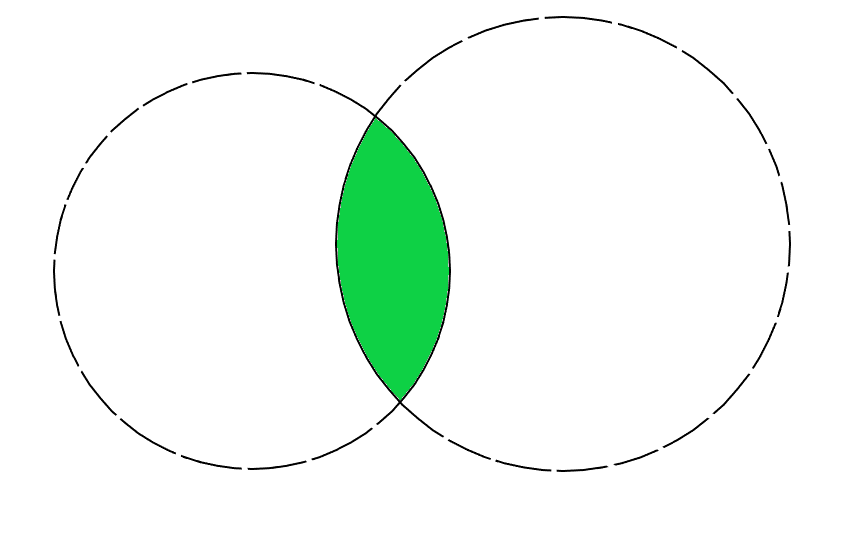
Let us call a lune of an edge the following lune:
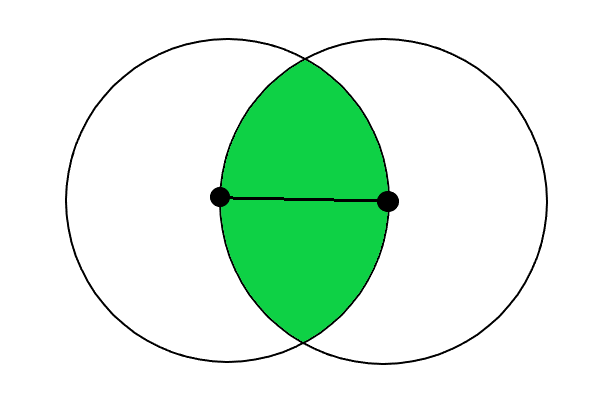
It is formed by two circles with centers at the edge endpoints, and radii equal to the Euclidean distance between the edge endpoints.
There is a property saying that in any MST for a full graph that can be drawn on a plane, there is no edge such that its lune contains any graph vertice. This property greatly reduces the amount of junctions to look for, and also can be adapted to the MST building, improving its performance even more, to O(N∙log(N)). As pointed out by Przemyslaw, “<…> lune property means that if we have edge |UV|, we can replace it either by |UW| or |VW| and it’s always better (assuming we’re sure W is always in the graph). Which means you can use it for MST as well.”
If re-reading this does not help, here are the pictures:
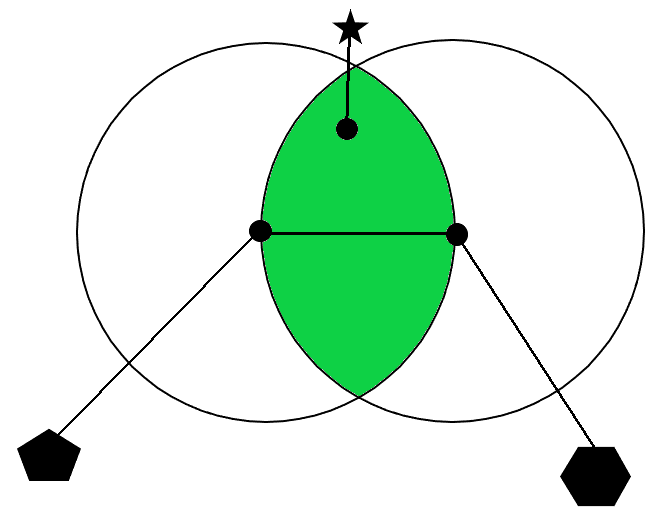
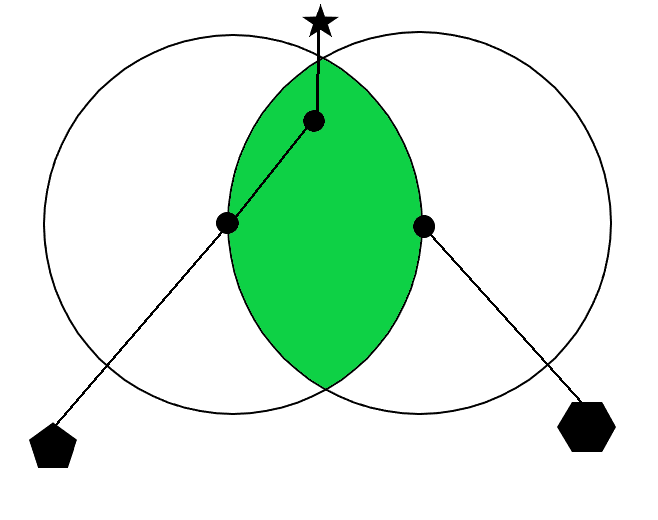
Here, the polygons mean the rest of the tree, and the long edge connecting the centers of the lune-forming arcs is replaced by a shorter edge. Note that the tree is still connected, because topmost polygon is connected to one of the bottom polygons before the improvement.
Resources
http://www.warme.net/david/pubs/dis.pdf
https://vlsicad.ucsd.edu/courses/geosteiner_study.pdf
Conclusion
The competition was very tough this time, partly because of the problem being mostly classical, partly because of the high randomness involved in the testing and scoring. Although the later was somewhat addressed by changing the scoring method early during the competition, the former was part of the game.
More than hundred participants managed to show an improvement over the MST algorithms and fight the randomness.
Now, after the results are finalized, I can say that randomness was not that big. The top of the leaderboard was taken by senior members. Congratulations to Wladimir Leite (wleite) for winning his 30th Marathon Match! Congratulation to 52 competitors who gained points in this hard match. Traditionally, Wladimir summarizes the points gained so far in the battle for the TCO trip. You can find them in the forums.
I would like to thank Catalin Stefan Tiseanu and Mariia Mykhailova for proof-reading a draft of this article. Another thank you is to all those participating in the post-match discussion on the forum for sharing their ideas. For me this is the most important, educational, and fun part of the marathon competition. And the last but not least thank you is to my mom who kindly reminded me to go to sleep before 2AM during the match.
gorbunov
Guest Blogger


