
|
In Part 1, we talked a bit about the simplest type of problem, where we are asked to write a single method that takes a set of inputs and returns a specified output. How do we approach more complicated types of problems?
Problems with callbacks
ContinuousSameGame is a good, simple, example of a problem that deals with callbacks. Note that, for each call to our method, we are given the full configuration of the board. One might assume this to mean that we can simply take the input we're given, and make a decision based upon that input. Certainly, we can, but we can also be a bit more clever to avoid doing the same work over and over again.
Suppose part of our solution involved determining which color(s) are most common on the board. If we keep this type of data in class-level variables then, following any move that did not completely clear any columns (and hence, did not introduce a new random column on the right), we can avoid having to recalculate these values. Similarly, if we have looked over the entire board and found several good candidate moves, and have only made moves that did not otherwise change the state of the board, then there is no need for us to find moves until we have exhausted our existing batch.
Some problems may involve writing multiple functions, implying that at least one callback is inevitable. A common scenario might be an init() function, and a next() function, where the init method is given basic parameters about the setup, and each successive call to the next method requests some type of move or selection to be made. Typically, the next method is passed only minimal information (in part, to reduce overhead on the server side), implying that a submission should include the necessary code to keep track of such data.
Using state machines
This "keeping track of data" is more formally known as implementing a state machine. Simply defined, a state machine is something that has a defined state, and ways to transition from one state to another.
One of the more complex implementations required by a submission came in this past TCO, with the TwoCardDraw problem. This problem required six methods, and it is still the record holder in that respect, by a wide margin. As alluded to in the problem statement, the problem was designed, in part, with the intention that a clever solution might able to glean information about the server's predefined strategy by carefully keeping track of how it behaved in various situations. In reality, most competitors decided that such an involved approach was unnecessary, and in fact, there probably would not have been enough data to usefully adapt before the end of a test case.
However, for illustrative purposes, consider how we might have proceeded with a learning type approach. We might want to keep track of how long each hand lasted, for instance. In other words, when did the server fold? (Or did we fold?) We are told within the problem statement that we need to determine things like that indirectly from how our methods are called. In particular, whenever newhand() is called, we can take that to mean that the previous hand ended. A simple approach might be to maintain a simple variable called currentPlay, where 1 = the initial round of betting, 2 = the draw, 3 = the second betting round, etc. Then, on each call to newhand(), we note the last value of our currentPlay, and reset it. We could expand this approach to use more variables to note other information about how many bets were placed, which cards we saw, or anything else we felt might be useful.
As an alternative to having to write callback-based solutions, library functions were introduced. With library functions, rather than the server calling a method in the competitor's solution, the submitted code can actually make calls directly to the server -- typically to request information, or make a move. Often, the number of times such a function is called will play a part in the scoring of the solution.
Problems involving randomness
Part of the idea of marathon problems is that it is generally impossible to get a perfect solution, at least before the sun burns out. One common element that is introduced to make problems more challenging is an element of randomness. This past TCO saw two problems, DensityImaging and LumberjackExam, that relied heavily upon this randomness to make the problems themselves interesting. How the two problems introduce randomness, however, and what that means in writing a solution, are very different.
In the case of DensityImaging, we know that each measurement is adjusted by a random amount that fits a Gaussian distribution. Simply put, this means the adjustment will typically center around 0, with more wild adjustments being less frequent. In theory, with a large enough sample size, the returned values (when performing an identical measurement) should all fit a perfect bell curve, and the mean value would be absolutely correct. Since taking more measurements reduces our score, though, it is impossible to make anywhere near enough measurements to be able to average out the results and hope to minimize the total error. However, a little experimentation could show that even taking the same measurement twice and averaging the results can help improve one's score. Further experimentation may show that, depending on implementation details, adding a third or fourth round of measurements would be too costly for the diminishing returns.
Bayes Theorem
In the case of LumberjackExam, where the probabilities and errors refer to yes/no values, we can take a more precise mathematical approach to dealing with the inaccuracy by using some rules that are formally demonstrated by Bayes' Theorem. The theorem can be stated in a variety of different ways, but here's the one I find most useful:
Suppose a set of conditions, A1, A2,..., An each independently suggest that a condition B exists with probabilities p1, p2,..., pn, then the overall probability that condition B exists is given by:
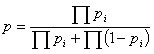
So how does this apply? Let's consider a real world example. Suppose that, of all people with long hair, 80% are computer programmers. Suppose also that of all the people who wear glasses, 70% are computer programmers. Now, suppose someone walks by who has long hair, and wears glasses. What are the chances he is a computer programmer?
At first glance, someone might confuse this with another type of problem and arrive at an answer of 94%. I'm referring to problems like, "There is a 70% chance of rain today, and an 80% chance of rain tomorrow. What are the chances that it rains today or tomorrow?"
The key difference here, in the example of the rain problem, is the word "or." It doesn't matter if it rains today, tomorrow, or both. When dealing with conditional probabilities that fall under Bayesian rules, that same "or" does not apply; that is, the two propositions are no longer independent events. The visually impaired, long-haired gentleman in question is either a programmer or he is not -- thus, either both conditionals are true, or both are false.
If both are true, then 70% * 80% = 56%. If both are false, and he is not a programmer, then we evaluate 30% * 20% = 6%. Now, notice that 56% + 6% does not add up to a full 100%. So, we divide both by 62% to scale the value appropriately. Thus, there is approximately a 90.3% chance this gentleman is a programmer.
There is one more important and useful detail of this basic equation. Though I will leave the formal algebraic proof as an exercise to the reader, compare what happens if we have three conditional probabilities (as opposed to just two), and one of them is the calculated overall probability based upon two or more conditionals. Perhaps not surprisingly, the result is the same. What this means for us is that, using Bayes' theorem, we can accurately keep track of the probability of something being true by repeatedly applying the theorem every time we get a new piece of information, without having to keep track of the individual conditional probabilities that we have previously collected.
In the example above, we already know the gentleman has a 90.3% chance that he is a programmer. If we were then to be told that whenever someone is carrying a laptop (and let's assume our friend is), that they have a 60% chance of being a programmer, we can then update our probability:
p = (0.903 * 0.6) / ((0.903 * 0.6) + (.097 * 0.4)) = 93.3%.
This is particularly useful in the lumberjack problem. Every time we make an observation, we calculate a conditional probability for each tree (which was included in that viewing) being infected. If any of those trees have already been viewed, then we can use the theorem to update our conditional probability for any of those trees, and can continue to do so with each new observation. And, in theory, we can continue doing so repeatedly, each time ending with a more accurate feel for if the tree is actually infected. In the case of this particular problem, we can make some observations about the effectiveness of looking at certain long distances, and may wish to only consider, say, the first five trees in front of us.
During the Intel competition series, the MessageReceiver problem had a similar conditional probability at work, in that each letter could either be transmitted correctly or incorrectly. Knowing this, it should come as no surprise that the winning solution relied heavily upon Bayes' theorem as well.
Putting it all together
There are many different approaches to Marathon Match problems. As always, the key thing to remember – and the single coolest thing about Marathon Matches, in my opinion – is that these problems are interactive. Rather than a "final answer," the best type of Marathon Match solution is more like a dialogue. As each test case progresses, your solution must keep track of its progress, and refine or shift its strategy accordingly. Good luck!
Interested in writing for TopCoder? We're looking for new educational tutorials and feature articles -- if you've got ideas, email them to editorial@topcoder.com.
