
|
Match Editorials |
Monday, March 19, 2007
Match summary
Fairly difficult medium and hard problems led to a relatively low scoring HS match. LynValente won the match with 1174.04 points, msg555 finished second with 1041.94 and AnonnymousT rounded out the top three with 775.53. Only three coders successfully solved the hard problem, and only two were able to solve all three problems.A good score on the easy problem was enough to advance. Congratulations to the 25 lucky competitors who won a place in the onsite finals!
The Problems
Kings

Used as: Division One - Level One:
Based on my own experience, I think that the most difficult part of this problem is separating the kings with unique names from those who have a namesake(s). Probably one of the most obvious ways to achieve this separation is just to count the number of occurences of each name in the given list. Map data structure provides a good aid here. After separation, we need to do a second pass over the list in order to enumerate the kings whose names occurs in the list more than once.
Value 250 Submission Rate 40 / 40 (100.00%) Success Rate 37 / 40 (92.50%) High Score neal_wu for 248.51 points (2 mins 12 secs) Average Score 223.85 (for 37 correct submissions)
C++ code follows:
template <class Ty, class Tx>
Ty cast(const Tx &x) {
Ty y; stringstream ss(""); ss<<x; ss.seekg(0); ss>>y; return y;
}
class Kings {
public:
vector <string> enumerate(vector <string> names) {
map <string, int> count1, count2;
int n, i;
n = names.size();
for (i = 0; i < n; i++) count1[names[i]]++;
for (i = 0; i < n; i++) if (count1[names[i]] > 1)
names[i] += " " + cast<string>(++count2[names[i]]);
return names;
}
};
DividingRectangle


Used as: Division One - Level Two:
There are six ways of dividing rectangle according to the rules described in the problem statement. They are all shown on Figure 1:
Value 500 Submission Rate 18 / 40 (45.00%) Success Rate 14 / 18 (77.78%) High Score gurugan1 for 390.61 points (15 mins 59 secs) Average Score 315.95 (for 14 correct submissions)
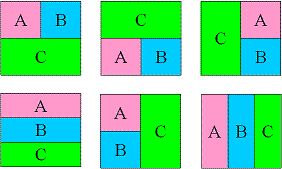
Figure 1. Ways of dividing.
So we just need to try each of these ways and bruteforce delimiter-positions between the smaller rectangles. Summing up the elements of the smaller rectangles can be done straightforwardly due to the low constraints.
Java code follows:
public long maxProduct(String[] rectangle) {
long[][] a;
long ret;
int n, m, i, j, k;
n = rectangle.length;
m = rectangle[0].length();
a = new long[n][m];
for (i = 0; i < n; i++)
for (j = 0; j < m; j++)
a[i][j] = rectangle[i].charAt(j) - '0';
ret = 0;
for (i = 0; i < m - 2; i++) for (j = i + 1; j < m - 1; j++)
ret = Math.max(ret, sum(0, 0, n - 1, i) * sum(0, i + 1, n - 1, j) *
sum(0, j + 1, n - 1, m - 1));
for (i = 0; i < n - 2; i++) for (j = i + 1; j < n - 1; j++)
ret = Math.max(ret, sum(0, 0, i, m - 1) * sum(i + 1, 0, j, m - 1) *
sum(j + 1, 0, n - 1, m - 1));
for (j = 0; j < m - 1; j++) for (i = 0; i < n - 1; i++)
ret = Math.max(ret, sum(0, j + 1, n - 1, m - 1) * sum(0, 0, i, j) *
sum(i + 1, 0, n - 1, j));
for (j = 0; j < m - 1; j++) for (i = 0; i < n - 1; i++)
ret = Math.max(ret, sum(0, 0, n - 1, j) * sum(0, j + 1, i, m - 1) *
sum(i + 1, j + 1, n - 1, m - 1));
for (i = 0; i < n - 1; i++) for (j = 0; j < m - 1; j++)
ret = Math.max(ret, sum(0, 0, i, j) * sum(0, j + 1, i, m - 1) *
sum(i + 1, 0, n - 1, m - 1));
for (i = 0; i < n - 1; i++) for (j = 0; j < m - 1; j++)
ret = Math.max(ret, sum(0, 0, i, m - 1) * sum(i + 1, 0, n - 1, j) *
sum(i + 1, j + 1, n - 1, m - 1));
return ret;
}
Function s(i1, j1, i2, j2) returns a sum of all elements between rows i1 and i2
and columns j1 and j2, inclusive.
GamesSchedule


Used as: Division One - Level Three:
It is not difficult to realize that this one can be solved by backtracking, but it is much more difficult to implement it quickly and correctly.
Value 1000 Submission Rate 6 / 40 (15.00%) Success Rate 3 / 6 (50.00%) High Score LynValente for 578.85 points (29 mins 9 secs) Average Score 537.26 (for 3 correct submissions)
Parameters for the backtracking function rec are:
- r - number of the game (number of the rows in the schedule table)
- c - number of the team (number of the rows in the schedule table)
- d - number of the unassigned colors left during the rth game
- e - experience of the team that plays in the rth game (e = -1 if it's unknown because none of the first c-1 teams is assigned to this game)
- cmask - binary mask of the colors. ith bit of cmask is set if and only if ith color is assigned to one of the first c-1 teams during rth game
- g[][] - original schedule
- n - number of teams
- k - number of colors
- ex[] - ex[i] contains the number of games played by ith team during the first r games
- col[][] - col[i][j] = 1 if ith team played for color j during the first r games, col[i][j] = 0 in the other case
C++ code follows:
vector <string> g;
int n, k;
int ex[5], col[5][5];
int rec(int r, int c, int d, int e, int cmask) {
if (c == n && d) return 0;
if (c == n) return rec(r + 1, 0, k, -1, 0);
if (r == n) return 1;
int ret, i;
ret = 0;
if (d && ex[c] < k && (e == -1 || e == ex[c]))
for (i = 0; i < k; i++) if (!((cmask >> i) & 1) && !col[c][i])
if (g[r][c] == '?' || g[r][c] == 'A' + i) {
ex[c]++;
col[c][i] = 1;
ret += rec(r, c + 1, d - 1, ex[c] - 1, cmask | (1 << i));
col[c][i] = 0;
ex[c]--;
}
if (g[r][c] == '?' || g[r][c] == '-') ret += rec(r, c + 1, d, e, cmask);
return ret;
}
class GamesSchedule {
public:
int howMany(vector <string> schedule, int _k) {
g = schedule;
n = schedule.size();
k = _k;
memset(ex, 0, sizeof(ex));
memset(col, 0, sizeof(col));
return rec(0, 0, k, -1, 0);
}
};
