
|
Match Editorials |
Monday, February 26, 2007
Match summary
On Monday, February 26, high school students entered the first round of the ultimate battle for the onsite spots of the 2007 TopCoder High School Tournament. The students from Gamma region were given a chance to compete first. With 51 students from Gamma registered for the tournament, 40 actually coming to compete, and 250 spots in the next round, the main goal for all the contestants was to have a positive score in the round.Thirty-eight contestants were successful in getting that positive score, led Burunduk3 from Saint-Petersburg Phys-Math Lyceum #30. He had the fastest time on all three problems and two successful challenges, separating him from the next closest competitor by a gap of almost 450 points.
Second place went to MrX from Yaroslavl 45, with crazzy from Kulachi Hansraj coming in third.
The Problems
TriangleConstruction

Used as: Division One - Level One:
There are many possible approaches to this problem, and most of them were acceptable within the given constraints. Probably the easiest of them is the brute-force option: consider all triples of sticks, and for each check whether they can form a triangle. From among these choose the triangle with greatest perimeter.
Value 250 Submission Rate 38 / 40 (95.00%) Success Rate 37 / 38 (97.37%) High Score Burunduk3 for 248.25 points (2 mins 23 secs) Average Score 238.08 (for 37 correct submissions)
To check whether the sticks with lengths a, b and c can form a triangle, we must check that the sum of lengths of two shorter ones is greater than the length of the longest. Alternatively we can check all three possible inequalities: a + b > c, b + c > a and c + a > b. These inequalities are known as triangle inequalities. Clearly, one of them corresponds to the required one, and the other two are trivially satisfied. The code follows:
public int greatestPerimeter(int[] l) {
int best = -1;
int n = l.length;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
for (int k = j + 1; k < n; k++) {
if (l[i] + l[j] > l[k] && l[j] + l[k] > l[i] && l[k] + l[i] > l[j]) {
if (l[i] + l[j] + l[k] > best) {
best = l[i] + l[j] + l[k];
}
}
}
}
}
return best;
}
Another approach is to sort the array beforehand. In this case we can check
only one inequality, since we know the order of the lengths. However,
an additional observation shows that in this case we need to check only successive
sticks.
Accordingly, let the array be sorted and the optimal solution be sticks with lengths l[i], l[j] and l[k] where i < j < k. Then l[k - 2] ≥ l[i], l[k - 1] ≥ l[j], and therefore l[k - 2] + l[k - 1] ≥ l[i] + l[j] > l[k], so the triangle with edges made of sticks with lengths l[k - 2], l[k - 1] and l[k] exists and is at least as good. The code for this approach follows.
public int greatestPerimeter(int[] l) {
Arrays.sort(l);
int best = -1;
int n = l.length;
for (int i = 2; i < n; i++) {
if (l[i - 2] + l[i - 1] > l[i]) {
if (l[i - 2] + l[i - 1] + l[i] > best) {
best = l[i - 2] + l[i - 1] + l[i];
}
}
}
return best;
}
SortingPhotos


Used as: Division One - Level Two:
For each photo i let us find a[i] - the number of photos that are smaller than it, and b[i] - the number of photos that it is smaller than. After that, checking whether the photo is large, small or average is straightforward. The code follows:
Value 450 Submission Rate 39 / 40 (97.50%) Success Rate 30 / 39 (76.92%) High Score Burunduk3 for 444.48 points (3 mins 10 secs) Average Score 397.11 (for 30 correct submissions)
boolean smaller(int w1, int h1, int w2, int h2) {
return w1 < w2 && h1 < h2;
}
public int[] sortPhotos(int[] w, int[] h) {
int n = w.length;
int[] a = new int[n];
int[] b = new int[n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (smaller(w[i], h[i], w[j], h[j])) {
a[i]++;
b[j]++;
}
}
}
int sm = 0;
int lg = 0;
for (int i = 0; i < n; i++) {
if (a[i] == 0 && b[i] > 0) {
lg++;
}
if (b[i] == 0 && a[i] > 0) {
sm++;
}
}
return new int[]{sm, n - sm - lg, lg};
}
MultiprocessorProgramming


Used as: Division One - Level Three:
First of all, consider the function
Value 1000 Submission Rate 29 / 40 (72.50%) Success Rate 9 / 29 (31.03%) High Score Burunduk3 for 929.39 points (7 mins 57 secs) Average Score 507.46 (for 9 correct submissions)
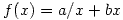 ,
where a > 0, b > 0.
Let us find the value of x that minimizes f. Transform f in the following way:
,
where a > 0, b > 0.
Let us find the value of x that minimizes f. Transform f in the following way:
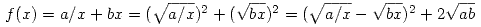 .
Since the square of a real number is non-negative, this value is at least
.
Since the square of a real number is non-negative, this value is at least
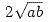 and is minimized when
and is minimized when
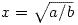 .
.
Now let us get back to our problem. Let the function relax(int n) calculate the time needed for executing the task on n processors, compare it to the best known value, and update it if necessary.
The time needed to execute the task onthe optimal number of processors is at least t0 + tp, since this value can be achieved using one processor. Therefore we can safely initialize the best known needed time as t0 + tp.
Following the considerations from the first paragraph, we deduce that the time needed to execute the parallelizable part of the task on several processors descends until n - 1 is approximately
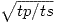 and grows after that. Therefore it is clearly irrelevant to use
more than
and grows after that. Therefore it is clearly irrelevant to use
more than 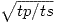 rounded up additional
processors. Since tp doesn't exceed 109, this value doesn't exceed
31623. So we can check n from 1 to
rounded up additional
processors. Since tp doesn't exceed 109, this value doesn't exceed
31623. So we can check n from 1 to
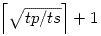 and call relax(n) for all of these values. Code follows:
and call relax(n) for all of these values. Code follows:
double best;
int opt;
int t0;
int tp;
int ts;
void relax(int n) {
double value = Math.max(t0, 1.0 * tp / (n - 1) + 1.0 * ts * (n - 1));
if (value < best) {
best = value;
opt = n;
}
}
public long optimalNumberOfProcessors(int t0, int tp, int ts) {
this.t0 = t0;
this.tp = tp;
this.ts = ts;
best = t0 + tp;
opt = 1;
for (int i = 2; i <= Math.sqrt(tp / ts) + 2; i++) {
relax(i);
}
return opt;
}
