
|
Match Editorials |
Thursday, December 13, 2007
Match summary
This match saw a tough hard problem with only one passing solution and even that was submitted with little time left. In addition to that, less than half of the submitted solutions were correct. In the end, zmy won the match by being the only one to solve all 3 problems, neal_wu came in second with fast easy & medium solutions + 225 points from challenges, PaulDB followed in third.
Even though SRM 383 took place at the exact same time, 7 coders attempted to compete in both. This proved not to be a great idea as only sim40_sh was able to increase his rating in both.
The Problems
SendingCards

Used as: Division One - Level One:
Value 250 Submission Rate 142 / 148 (95.95%) Success Rate 127 / 142 (89.44%) High Score exod40 for 249.55 points (1 mins 13 secs) Average Score 224.79 (for 127 correct submissions)
In this problem all one had to do was count the number of times a friend sent a card and did not receive one in return or vice versa. Most people who failed to solve this problem did not check the second condition and therefore failed on a simple case:
NNThe correct answer is 1. Java solution follows:
YN
public class SendingCards {
public int howMany(String[] friends) {
int result = 0;
for(int i = 0; i < friends.length; ++i)
for(int j = i + 1; j < friends.length; ++j)
if(friends[i].charAt(j) != friends[j].charAt(i))
++result;
return result;
}
}
CommonFactors


Used as: Division One - Level Two:
Value 500 Submission Rate 97 / 148 (65.54%) Success Rate 44 / 97 (45.36%) High Score maciejk for 493.20 points (3 mins 20 secs) Average Score 338.50 (for 44 correct submissions)
In this problem the most straightforward solution is to calculate all distinct factors for every number, count the number of occurrences over all numbers and then return the largest solution (not equal to 1) with most occurrences. The easiest way to get the factors of N is to try for every i (1 <= i2 <= N) whether i divides N. If it does then it is a factor of N and so is N / i. Just take care not to count any factors of N more than once. The following C++ solution does just that:
struct CommonFactors {
int mostCommon(vector <int> n) {
map <int, int> f;
for(int i = 0; i < n.size(); ++i)
for(int j = 1; j * j <= n[i]; ++j)
if(n[i] % j == 0) {
if(j != 1)
++f[j];
if(j * j != n[i])
++f[n[i] / j];
}
int result = 0, count = 0;
for(map <int, int>::iterator i = f.begin(); i != f.end(); ++i)
if(i->second >= count) {
result = i->first;
count = i->second;
}
return result;
}
};For an alternative solution see Loner's code.
ThreeWatchtowers


Used as: Division One - Level Three:
Value 1000 Submission Rate 15 / 148 (10.14%) Success Rate 1 / 15 (6.67%) High Score zmy for 412.26 points (54 mins 16 secs) Average Score 412.26 (for 1 correct submission)
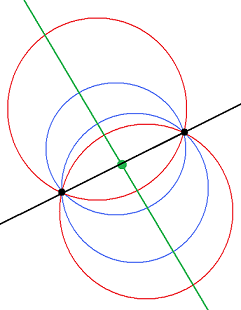
First we are going to prove the following property. We always can construct an optimal solution in such way that each of the towers is located either at a point of interest, or in such way that at least 2 points of interest will lie on the border of watchtower's field of view. Really, if a tower sees exactly one point, we can always put the watchtower exactly at this point. If a tower sees at least two points, then we can move it in some direction until at least 2 points will lie on the border of its field of view.
What you want to do with a watchtower is to put it between 2 points such that it is equally far from both of them and is as far as possible. This ensures that it can cover a maximum amount of other points. This means that all such points will lie on the green line. If the distance between the points is equal to the diameter of the watchtower’s visibility range then there will be exactly one such point, otherwise there will be either infinite amount (if the points are at the same location) or 2 as shown on the picture by the blue circles for one watchtower and with red circles for another watchtower.
This C++ solution uses bitmasks to represent sets of points of interests visible from watchtowers. Operator | is used to add an element to a set and __builtin_popcount() is GCC function that counts the number of bits set (in this context: the number of points of interest visible from a certain watchtower). To get more information about playing with bits see bmerry’s article A bit of fun: fun with bits.
template <typename T>
inline T sqr(T a) {
return a * a;
}
struct ThreeWatchtowers {
int N;
// count the number of points of interest visible from point (cx,cy)
int getMask(vector <int> &x, vector <int> &y, double cx, double cy, int R) {
int result = 0;
for(int i = 0; i < N; ++i) {
double dist = sqrt(sqr(x[i] - cx) + sqr(y[i] - cy));
if(dist <= R + 1e-9)
result |= (1 << i);
}
return result;
}
// get bitmasks of all interesting placements
vector <int> masks(vector <int> &x, vector <int> &y, int R) {
// case1: no points of interest can be seen
vector <int> result(x.size() + 1);
// case2: the watchtower is placed at a point of interest and can only see
// points at the exact same location
for(int i = 0; i < N; ++i)
for(int j = 0; j < N; ++j)
if(x[i] == x[j] && y[i] == y[j])
result[i] |= (1 << j);
// case3: try to place a watchtower between each pair of points
for(int i = 0; i < N; ++i)
for(int j = i + 1; j < N; ++j) {
int sq = sqr(x[i] - x[j]) + sqr(y[i] - y[j]);
// if a watchtower between points i & j can not possibly
// see both at once then try next points
if(sq > sqr(2 * R))
continue;
double cx = (x[i] + x[j]) / 2.0;
double cy = (y[i] + y[j]) / 2.0;
double dist = sqrt(sq);
double pdist = sqrt(sqr(R) - sq / 4.0);
double nx = (x[j] - x[i]) / dist;
double ny = (y[j] - y[i]) / dist;
result.push_back(getMask(x, y, cx - pdist * ny, cy + pdist * nx, R));
result.push_back(getMask(x, y, cx + pdist * ny, cy - pdist * nx, R));
}
return result;
}
int maximumCoverage(vector <int> x, vector <int> y, vector <int> view) {
N = x.size();
vector <int> a = masks(x, y, view[0]);
vector <int> b = masks(x, y, view[1]);
vector <int> c = masks(x, y, view[2]);
int result = 0;
// use the best combination of watchtower locations
for(int i = 0; i < a.size(); ++i)
for(int j = 0; j < b.size(); ++j)
for(int k = 0; k < c.size(); ++k)
result = max(result, __builtin_popcount(a[i] | b[j] | c[k]));
return result;
}
};
