
|
Match Editorials |
Saturday, November 10, 2007
Match summary
This match saw 80 coders, 11 of them newcomers. Coders were faced with an easy problem set - 13 of them solved correctly
all three problems. Some implementations of the easy problem should have covered border case, but didn't which resulted in successful
challenges and failed system tests. After the easy problem, most of coders stepped onto the medimum one, where
mirosuaf very soon came up with sorrect solution. It seems
some coders took the hard problem too lightly, which resulted in several resubmits
(fpavetic had to resubmit twice).
Thanks to fast solutions for all problems and two successful challenges
Loner won the match, followed by
neal_wu who submited the hard problem a bit slower
and finished the challenge phase without extra points. Thanks to successful challenges,
sluga beat
Zuza, took third place and became red.
The Problems
YoungBrother

Used as: Division One - Level One:
Value 250 Submission Rate 70 / 80 (87.50%) Success Rate 55 / 70 (78.57%) High Score neal_wu for 249.48 points (1 mins 18 secs) Average Score 219.21 (for 55 correct submissions)
Like problem statement says, John's brother can perform two operations: add new line and delete new line. We will
label those with <enter> and <backspace>. Let's see what happens with chars when brother presses something.
Suppose text in the editor is
{"abc", "defg"}
In the first case, after brother's actions, it could be
{"abc", "d<enter>efg"} which is equal to {"abc", "d", "efg"}
or in the second case
{"abc", "<backspace>defg"} which is equal to {"abcdefg"}.
John's brother hasn't deleted any chars, so there are same chars after his actions.
It is obvious (and the most important part of the solution) that chars don't change order (if char x was before y in original
text, it will always remain before y, in every editor state). If you put all chars in one line,
no matter how many times brother pressed <enter> or <backspace> (even zero times), that line
will always be same. So, concatenate all
// concat all strings in lines
String ssum = new String("");
for (int i = 0; i < lines.length; i++)
ssum += lines[i];
String[] ret = new String[n];
// take substring of length k and add into result
for (int i = 0; i < n; i++){
ret[i] = ssum.substring(0, k);
ssum = ssum.substring(k);
}
return ret;
lines = {"", "", ""}, n = 10, k = 0 is.
For a nice and clean implementation you can see _sunrise's
code.
DriveCar


Used as: Division One - Level Two:
Value 500 Submission Rate 59 / 80 (73.75%) Success Rate 39 / 59 (66.10%) High Score mirosuaf for 497.17 points (2 mins 8 secs) Average Score 381.34 (for 39 correct submissions)
I will describe two ways of solving this task.
First approach:
During each turn, car can step only closer to the end of the road, so minimum number of changing lanes depends only
on steps done over cells which are closer to start (named cells with lower index). Let DP[i][j] be a
minimum number of changing lanes driving the car from start position to i-th cell of j-th lane (0-based). If i-th cell
of j-th lane contains an obstacle, set DP[i][j] to infinity.
Then you can define recurrent relation:
DP[i][j] = min(DP[i][j], DP[i - 1][j]) - car keeps driving on same lane
DP[i][j] = min(DP[i][j], DP[i - 1][j + 1] + 1) - car turned right on the last lane. Of course, this
is possible only if j represents lane 0 or 1
DP[i][j] = min(DP[i][j], DP[i - 1][j - 1] + 1) - car turned left on the last lane. This
is possible only if j represents lane 1 or 2
Process three by three cells, starting from the leftmost ones. You should only handle all three cells at position 0, what
is actually initial state.
Car starts from second lane at position 0 - initialize DP[0][1] to zero because car didn't make any
lane changes. Cells at position 0 in first and third lane are not reachable, so they shouldn't be processed - you can just
set DP[0][0] = DP[0][2] = infinity. According
to recurrent relation, proceed to cells with greater index, but be careful, don't make car crash - don't drive car out of
the road and watch out about obstacles. Following solution in Java:
int n = road[0].length();
int[][] dp = new int[n][road.length];
int inf = 1 << 30;
for (int i = 0; i < n; i++)
for (int j = 0; j < 3; j++)
dp[i][j] = inf;
dp[0][1] = 0;
for (int i = 1; i < n; i++)
for (int j = 0; j < 3; j++)
if (road[j].charAt(i) == '.'){
// car can continue driving on the same lane
dp[i][j] = dp[i - 1][j];
// car can go right
if (validPlace(j + 1))
dp[i][j] = Math.min(dp[i - 1][j + 1] + 1, dp[i][j]);
// car can go left
if (validPlace(j - 1))
dp[i][j] = Math.min(dp[i - 1][j - 1] + 1, dp[i][j]);
}
// take the minimum of last square of all three lanes
int ret = Math.min(dp[n - 1][0], Math.min(dp[n - 1][1], dp[n - 1][2]));
if (ret == inf)
return -1;
else
return ret;
Second approach:
Road (lanes and cells) and moves can be represented as a weighted graph. Each cell can be represented as vertex and each move
as edge, what is actually connection between neighbours cells - cell with lover index -> cell with greater index.
Note that edge is directed - differ in and out edge. Cell at i-th position of j-th lane (marked (i, j)) should be
connected with the others cells in the following manner:
- If cell contains an obstacle, don't add any out edge from vertex which represents that cell
-
If cell is a part of open road, then consider two cases:
- if car changes lane, add an edge weight 1 (1 lane change) to cells at position i+1 of lanes j-1 and j+1 - an out edge from (i, j) -> (i+1, j-1) and from (i, j) -> (i+1, j+1). Just be careful that next lane exists (i.e. if j=0, you should connect cell only with cell from lane 1, but if j=1, you should connect cell with cells from lane 0 and lane 2).
- if car keeps driving on same lane, add an edge weight 0 (car doesn't change lane) from current cell to the next cell (cell with greater index) in a same lane - (i, j) -> (i+1, j).
With small modification on graph, you can get final information in only one vertex, not in three rightmost. Actually, you should add vertex more, named resultVertex. Add an out edge weight 0 from each of the rightmost cells to resultVertex - if l is a number of cells in each lane, you should add (l-1, 0) -> resultVertex, (l-1, 1) -> resultVertex and (l-1, 2) -> resultVertex. Take a look at image bellow to make it clear.
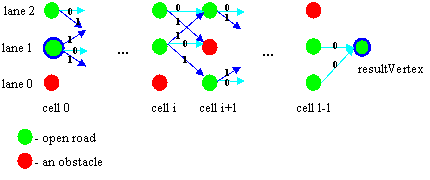
Most of coders solved this problem using first approach. See ahyangyi's solution for a clean implementation of the the first approach. Hornax's used the second approach to come up with a good solution. You can see it here. DogField


Used as: Division One - Level Three:
Value 1000 Submission Rate 26 / 80 (32.50%) Success Rate 15 / 26 (57.69%) High Score Loner for 739.88 points (18 mins 14 secs) Average Score 559.91 (for 15 correct submissions)
Low constraints suggests that you can use brute-force to solve this task, or at least a part of it.
We can divide this task into two parts.
At the first part of task, let's find the smallest number of seconds between dog and dog-house
for all dog - dog-house pairs. One move between adjacent squares costs dog 1 second. Again, you can represent field
as a graph. Each square will play role of a vertex. If squares a and b are adjacent, add an undirected
edge in the graph between vertices which represents a and b. Because one move costs 1 second, set the weight
of all edges to 1. Shortest path from some dog to some dog-house equals the smallest number of seconds which dog
can spend to come into dog-house. Once you make a graph, run the shortest path algorithm d times, each time
starting with a new dog. This graph is sparse (each vertex has at most 4 neighbours), so you can speed by using adjacency
list instead of adjacency matrix. Since all edges have same weight, you can use BFS to find shortest paths. Just be careful
about rules given in the statement - do not relax edges from squares which contain rock or dog-house.
Once you find all shortest paths, step onto brute-force. Assign exactly one dog-house to each dog, and vice versa. Also,
before you assign some dog-house to the dog, make sure that dog-house is reachable by that dog. For each assignment find
sum of all shortest paths between each dog and dog-house which is assigned to it. Compute sum for every assignment
(two assignments are different if there exists a dog which has two different dog-houses assigned). From all sums take the
smallest one and return it. If there is no assignment in which you can assign all dog-houses, return -1. Each assignment
represents one permutation of dog-houses. For 10 dogs, there will be 3,628,800 permutations what is enough to pass within
time limit - fix all dogs, permute all dog-houses and to i-th dog assign i-th dog-house from permutation.
See ikicic's
solution for a clean
implementation.
This problem can be solved using dynamic programming with bitmask. In this case, DP[i][mask] is
a minimum sum that last i dogs hide into dog-houses which are enumerated in mask.
See Zuza's
solution for a clean
implementation of this kind a solution. Btw, this solution is faster than a previous one.
