
|
Match Editorials |
Monday, December 18, 2006
Match summary
With 150 great high-school coders competing, this HS SRM was an exciting event. The competition started with a high number of fast submissions on the easy problem and, by the end of the coding phase, a reasonable number of medium and hard submissions were in. The challenge phase proved to be quite eventful, with many easy submissions coming down. As the dust settled, Weiqi finished on top by a wide margin, with the highest scores on the medium and hard and a great challenge phase. Loner finished second and turned red in the process. In third came tourist, who delivered an impressive performance in the challenge phase that made up for his resubmission of the hard. ahyangyi and zmy rounded out the top five. Congratulations to all the participants!
The Problems
AnswerEvaluation

Used as: Division One - Level One:
Most of the coders who failed this problem misinterpreted the statement and incorrectly counted occurrences of a keyword as substrings of words from the answer. Unfortunately, none of the examples helped to clarify this matter. In situations like this, if you are not sure about an aspect of the problem statement you shouldn't hesitate to ask the admins for clarifications.
Value 250 Submission Rate 141 / 150 (94.00%) Success Rate 84 / 141 (59.57%) High Score MB__ for 248.22 points (2 mins 24 secs) Average Score 209.01 (for 84 correct submissions)
A solution to this problem could start by splitting the answer into a list of words. This step is not really necessary but can greatly simplify the rest of the solution. In C++, this could be done with istringstreams. In Java and C# one could use the method split.
Next we have two approaches to choose from. The first one, which is more elegant and less error-prone, is to loop over all keywords and search for them in the list of words built from the answer. When we find a keyword present in the list, we add its score to the result. See SpaceFlyerís solution for a clean C++ implementation, Achtung-Achtung's solution for a Java one.
The second approach was to iterate over the words in the answer and look for them in the keyword list. In this solution one has to make sure that a keyword's score is not added with each of its occurrences in the word list. For a C# example of this approach see hildi's solution.
AnagramCompletion


Used as: Division One - Level Two:
There are two parts to this problem. First we need to find the letters to place in each wordís empty spots. Then we have to find the order in which these letters must be placed and handle the tie-breaking rules.
Value 550 Submission Rate 96 / 150 (64.00%) Success Rate 76 / 96 (79.17%) High Score Weiqi for 522.17 points (6 mins 37 secs) Average Score 361.41 (for 76 correct submissions)
For the first part, notice that if two words are anagrams, the number of occurrences of one letter in the first word is equal to the number of occurrences of this letter in the second word. For example, in the anagrams "BACACA" and "CAABAC" the letter 'A' appears three times in both words while the letter 'B' appears once in each. So, if we find that the letter 'L' appears three times in word1 and only once in word2, we have to place two more 'L's in the second word. In this way we can find the number of appearances of each letter in the desired anagrams. However, empty spots may still remain in both words. Since we are asked to break ties alphabetically, we will fill these empty spots with the letter 'A'. As an example, consider the words ".AC.A.B.BC" and "B..D.BB.A.":
- 'A' appears two times in the first word and one time in the second word, so it must appear one more time in word2
- 'B' must appear one more time in word1
- 'C' must appear two times in word2
- 'D' must appear once in word1
Now that we know the letters we must place in the empty spots we must determine how to handle the tie-breaking rules. This step is easy: we scan each word from left to right and fill each spot with the alphabetically smallest letter available. In the example above, we will complete the first anagram by filling the first two empty spots with the letter 'A' and the last two with the letters 'B' and 'D' (in this order). We do the same for the second word, and we return the strings "AACAABBDBC" and "BAADABBCAC".
For a clean implementation of this approach see Weiqi's solution.
SwampyLands


Used as: Division One - Level Three:
With its geometric nature, this problem at first seems really tough. However, observing that the sides of the rectangles representing swampy lands are parallel to the axes simplifies the problem significantly.
Value 1000 Submission Rate 21 / 150 (14.00%) Success Rate 13 / 21 (61.90%) High Score Weiqi for 873.81 points (11 mins 7 secs) Average Score 546.59 (for 13 correct submissions)
A first approach would be to treat the farm as a large grid, with a grid cell corresponding to a square region with the side equal to one unit. The cell at column x from row y would correspond to the square with the lower right corner at (x, y) and the upper left corner at (x+1, y+1). Then we mark each grid cell corresponding to a unit square contained in some rectangle piece of a swampy land, obtaining a binary matrix (with entries 0 or 1). Since we are not given any bounds for the farm, this looks like a matrix with an infinite number of rows and columns. However, we are only interested in the submatrix containing the given swampy lands, since all other entries will be unmarked (or 0). We will also keep two exterior rows and columns with unmarked entries for delimiting an exterior region. Having this matrix we can use a flood-fill algorithm to find the surrounded regions. There are two approaches. The more elegant one starts from the exterior region and finds all cells connected to it. The remaining unmarked cells are part of surrounded regions, so we add their area to the final result. A second approach would be to iterate over all unmarked cells and see if they are connected to the exterior. If not, we add their area to our result. Reference implementations for both versions are given in the last paragraph.
This looks easy, doesnít it? However, we have not finished yet. A look at the constraints suggests that our grid may be too large to fit in the memory limit and the algorithm will take too much time to execute. To handle this we will resort to a trick that may prove useful in other problems, and compress grid cells of the same type to a single grid cell. What does this mean? Take a look at the picture below:
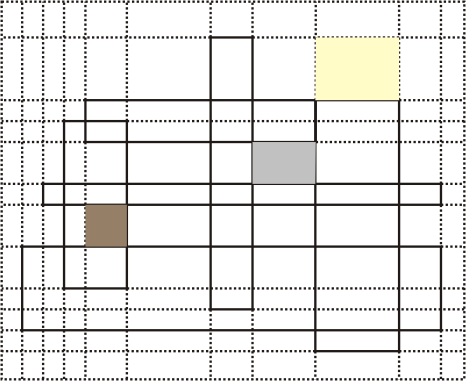
All cells contained in the colored regions can be considered of the same type. Since no rectangle from the input intersects those regions, if one cell from a region is surrounded, all cells from the same region are surrounded. All cells contained in a region are either swampy, surrounded or exterior. After compressing the regions in the picture above into grid cells, we have a new, much smaller grid.
If we let N denote the number of rectangular pieces of swampy land, this grid will have at most 2N+1 rows and at most 2N+1 columns. This easily fits in the memory limit, and the flood fill algorithm is fast enough.
In his solution, gooooodle implemented the flood fill algorithm recursively. Other coders used breadth first search, as Loner did in his solution. MB__ used the second approach mentioned above (code here).
