
|
Match Editorials |
Monday, August 21, 2006
Match summary
This match proved to be harder then usual. While almost all participants successfully solved the 250 problem, the other two problems appeared to be quite difficult.
Nevertheless, YuJieLu, a newcomer from China, won the match with the fastest times on the 550 and 950 problems, and an amazing nine successful challenges. He was followed by his Chinese fellows ahyangyi, hupo001, wintokk, and Weiqi. lexgas from Romania, in third place, was the only European in the top six.The Problems
IndictDates

Used as: Division One - Level One:
The straightforward approach to solving this problem is to simulate the process described in the problem statement. Let's start at year one and iterate years until we reach one with given indict, circle to the Sun and circle to the Moon. But if you want to win the Shortest-250-Competition, so popular at the TopCoder forums, you should use another approach, based on the Chinese remainder theorem. Note, that since 15, 19 and 28 are coprime numbers, the Indict system establishes the one-to-one correspondence between years in range from 1 to 15*19*28 = 7980 and its indict notation.
Value 250 Submission Rate 87 / 93 (93.55%) Success Rate 86 / 87 (98.85%) High Score Burunduk3 for 248.81 points (1 mins 58 secs) Average Score 223.62 (for 86 correct submissions)
Let inv(a, b) be such an integer c, that ac mod b = 1. Consider the expression:
Y = inv(28*19, 15)*28*19*(indict-1) + inv(15*19, 28)*15*19*(circleSun-1) + inv(28*15, 19)*28*15*(circleMoon-1)
Note, that Y mod 7980 = indict-1, Y mod 7980 = circleSun - 1 and Y mod 7980 = circleMoon - 1.
In this case (Y mod 7980) + 1 is the answer for the problem. It's easy to see that inv(28*19, 15) = 13, inv(15*19, 28) = 17 and inv(28*15, 19) = 10. Being simplified, it gives us a beautiful solution:
struct IndictDates{
int getYear(int indict,
int circleSun,int circleMoon){
return
(6916*indict+4845*circleSun+4200*circleMoon-1)%7980+1;
}
};
DistinctDice


Used as: Division One - Level Two:
Value 550 Submission Rate 51 / 93 (54.84%) Success Rate 17 / 51 (33.33%) High Score YuJieLu for 532.32 points (5 mins 12 secs) Average Score 401.15 (for 17 correct submissions)
Fisrt of all let's enumerate die's sides in the order they are mentioned in the problem statement:
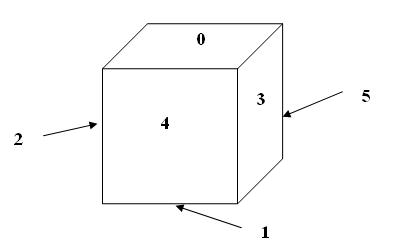
The first task we need to fulfill is to learn how to rotate the die. You need some imagination to see that we can carry out any rotation of the die by combining only two basic rotations, shown on the figure below.

Since we have enumerated the die's sides, let's represent each of these rotations as a permutation. The i'th element of the permutation will be the side that will appear at the position i after applying the rotation. In this case, rotateRight = {2, 3, 1, 0, 4, 5} and rotateBack = {4, 5, 2, 3, 1, 0}. Let's implement the ApplyRotation procedure, that takes string die and int[] permutation and applies the rotation of the die according to the permutation. The pseudocode follows:
string ApplyRotation(string die, int[]
permutation){
string result = "";
for( i = 0; i < 6; i++)result+=die[permutation[i]];
return result;
}
Now, for each die, let's apply all possible rotations and select
one with the lexicographically first notation. Let's call such a notation a normal form of the die. In this case,
we can compare
any two dice by their normal forms.
Now the pseudocode of the solution looks as follows:
int getDistinct( string[] givenDice ){
for( i = 0; i
givenDice[i] = normalForm(givenDice[i]);
sort(givenDice);
int Answer = 1;
for( i = 1; i < givenDice.size(); i++)
if(givenDice[i]!=givenDice[i-1])
Answer++;
return Answer;
}
Finally, we need to implement the normalForm procedure.
Notice that the die's positon is unambiguously determined by it's front
side and top side. (In this case, any die can occupy at most 6*4 = 24 different
positions.) To generate all the rotations, we need to set each side of
the die as it's front side and then apply rotateRight 4 times.
Let's see the pseudocode:
string normalForm(string die){
string result = die, tmp;
for(int i = 0; i < 4; i++){
die = ApplyRotation(die, rotateBack);
tmp = fourRightRotations(die);
if(tmp < result)result = tmp;
}
//now all the rotations with side 1, 5, 0, and 4 at front are
handled
die = ApplyRotation(die, rotateBack);
die = ApplyRotation(die, rotateRight);
die = ApplyRotation(die, rotateBack);
//now side 3 at front
tmp = fourRightRotations(die);
if(tmp < result)result = tmp;
die = ApplyRotation(die, rotateBack);
die = ApplyRotation(die, rotateBack);
//now side 2 at front
tmp = fourRightRotations(die);
if(tmp < result)result = tmp;
return result;
}
At last, here is the fourRightRotations function, which
applies right rotation four times and returns the lexicographically first among them:
string fourRightRotations(string die){
string result = die;
for(int j = 0; j < 4; j++){
die = ApplyRotation(die, rotateRight);
if(die <
result)result = die;
}
return result;
}
Another approach of recursive generation of the rotations was used by
YuJieLu. See his
solution for the details.Dragon


Used as: Division One - Level Three:
Value 950 Submission Rate 28 / 93 (30.11%) Success Rate 8 / 28 (28.57%) High Score YuJieLu for 868.07 points (8 mins 53 secs) Average Score 666.22 (for 8 correct submissions)
In this problem we need to use dynamic programming twice (read this tutorial if you are unfamiliar with it). To compute the probability of the knights' win, we need to predict the dragon's behavior. To do this, we need to know when it is worthwhile for the dragon to attack and when it is better to skip and hide in the cave. At first, for all possible amounts of knights and dragon's heads that may appear after dragon's turn, let's determine the probability of knight's victory. Let K[i][j] be the probability of victory of i knights over j-headed dragon. This is quite simple - see the following pseudocode:
for i = 0 to k do K[i][0] = 1.0;Now all we need is for each configuration to decide if it is profitable for the dragon to atack the knights. Let's define D[a][b] as the probability of the knights' win if the a-headed dragon faces b knights (and the dragon still may attack). In this case the dragon has two options. First, he can skip and knights will win with probability K[a][b]. Otherwise, with probability of probDragon he will kill a knight or loose one head otherwise. In the first case knights will win with probability of D[a][b - 1], and in the second their win will occur with probability of D[a - 1][b]. This means, the cumulative probability of their win is Pab = (probDragon* D[a][b - 1] + (1 - probDragon) * D[a - 1][b]). Therefore, the dragon will attack only if Pab will be smaller than K[a][b], since he wants to minimize the knights' chances to win. The following pseudocode calculates D[i][j]'s (the answer to our problem is D[heads][knights]):
for i = 1 to k do
for j = 1 to h do
K[i][j] = probKnight * K[i-1][j-1] + (1 - probKnight) * K[i - 1][j];
for i = 1 to k doYou can also see Burunduk2's solution for a clear implementation of this approach. As an implementation detail, you can solve the problem with only one two-dimensional array. To do this you need to store values of D[i][j] in the array K[i][j], overwriting corresponding values of K[i][j] (clearly, the answer to our problem will be K[heads][knights]):
for j = 1 to h do
D[i][j] = min(K[i][j], probDragon * D[i-1][j] + (1 - probDragon) * D[i][j-1]);
for i = 1 to k do
for j = 1 to h do
K[i][j] = min(K[i][j], probDragon * K[i-1][j] + (1 - probDragon) * K[i][j-1]);
