
|
Match Editorials |
Monday, August 7, 2006
Match summary
One more match has passed under the banner "burunduk's the best." Burunduk is the Russian word for chipmunk, so one could say it was a regular "chipmunk day" on TopCoder. Burunduk3 won the match thank to amazing 990.01 points for the hard problem. icanadi finished second only due to a frustrating mistake – now he surely knows that submitting the same code twice can cost a victory. tomekkulczynski rounded out the top three.
The Problems
Fractile

Used as: Division One - Level One:
Value 250 Submission Rate 120 / 125 (96.00%) Success Rate 96 / 120 (80.00%) High Score Zuza for 248.97 points (1 mins 50 secs) Average Score 221.23 (for 96 correct submissions)
This problem is an example of a usual Div2Easy problem with a straightforward solution. First useful thing to do is to sort the given array. Now assuming the elements of the array are indexed 0-based, the index of the desired element can be calculated using the following formula: z = n * p / 100, where n is the number of elements in the given array. There are two corner cases here:
- if n * p / 100 has no real part, then z must be decreased by one;
- if p is zero, then z is zero.
public int fractile(int[] x, int p) {
int n, z;
Arrays.sort(x);
n = x.length;
z = n * p / 100;
if (n * p % 100 == 0 && z > 0) z--;
return x[z];
}
This approach probably is not the best to use during the contest, because of the mentioned corner cases. Many coders used the various iterative algorithms in order to get as much points as possible.
Cannons

Used as: Division One - Level Two:
Value 500 Submission Rate 105 / 125 (84.00%) Success Rate 96 / 105 (91.43%) High Score thoconracroi for 486.95 points (4 mins 40 secs) Average Score 394.71 (for 96 correct submissions)
Direction of any particular cannon exerts no influence to any of the other cannons, so this problem can be solved greedy. For each cannon try directions in the alphabetical order of their abbreviations until an allowed direction is reached. If there is no allowed direction for at least one cannon, return the empty string.
Java code follows:
static public String getDirections(int[] x, int[] y) {
int n, i, j;
String ret;
n = x.length;
ret = "";
for (i = 0; i = n) { ret += "D"; continue; }
// try left ('L')
for (j = 0; j = n) { ret += "L"; continue; }
// try right ('R')
for (j = 0; j x[i]) break;
if (j >= n) { ret += "R"; continue; }
// try up ('U')
for (j = 0; j y[i]) break;
if (j >= n) { ret += "U"; continue; }
// no solution
return "";
}
return ret;
}
SwitchingBits


Used as: Division One - Level Three:
Value 1000 Submission Rate 96 / 125 (76.80%) Success Rate 84 / 96 (87.50%) High Score Burunduk3 for 990.01 points (2 mins 51 secs) Average Score 856.35 (for 84 correct submissions)
There is no reason to invert two intersecting substrings because it is always possible to invert only the parts, which are located outside of the intersection instead, in no more than two operations.
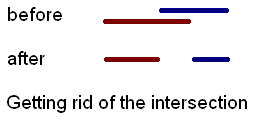
There is also no reason to change one to zero trying to obtain the all-ones string and no reason to change zero to one trying to obtain the all-zeroes string. So you just need to calculate the number of the groups of the consequent zeroes and the number of the groups of the consequent ones. Then return the smallest of this numbers. Burunduk3's solution is not only the fastest, but also probably the most elegant.
