Challenge Overview
Single-cell-omics Trajectory Inference (TI) methods are essential tools for the analysis of cellular dynamic process and to understand gene regulation. More than 60 methods have been developed and the list still keeps growing. It's time to bring fresh ideas to this emerging and exciting field and keep improving.
Preregistration Start Date: 7th June, 2019
Challenge Launch / Live Date: 21st Dec, 2019
Challenge Prizes: $8,000 / $6,000 / $4,000 / $2,000 / $1,000 / $750 / $750 / $500 / $500 / $500
Recent technological progress has allowed us to measure the current state of a cell. In this competition we focus on the transcriptome of a cell (i.e. the expression of the genes), which can be analyzed with single-cell RNA-sequencing technologies. In recent years these techniques have scaled up to being able to assess the expression (i.e. activity) of thousands of genes within tens of thousands of cells.
The state of a cell often changes gradually, and so does its transcriptome. In fact, cells are constantly changing based on external and internal stimuli. These can include:

The topology of a trajectory can range from very simple (linear or circular) to very complex (trees or disconnected graphs).

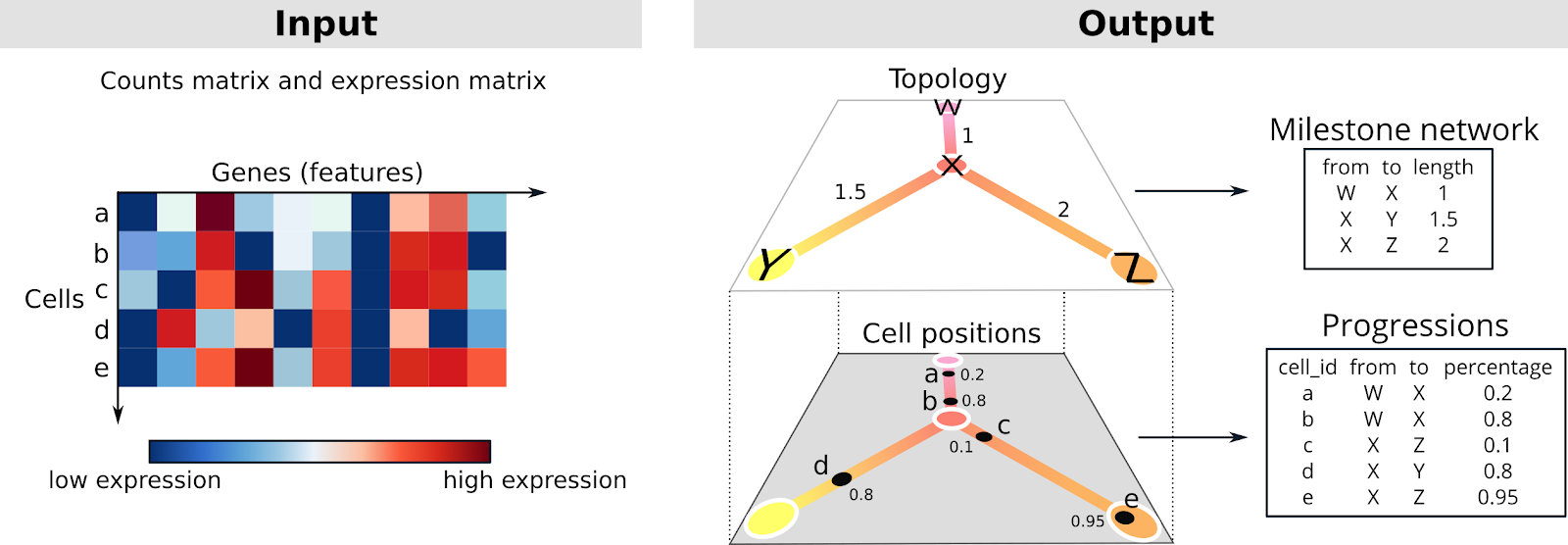
The topology is a graph structure, in this context called the milestone network as it connects “milestones” that cells pass through. Each edge within the milestone network can only be present once, and every edge has an associated length, which indicates how much the gene expression has changed between two milestones.
The cells are placed at a particular position of this milestone network. We represent this as “progressions”, where each cell is assigned to an edge and a percentage indicating how far it has progressed in that edge.
You must not submit more often than 2 times a day. The submission platform does not enforce this limitation, it is your responsibility to be compliant to this limitation. Not observing this rule may lead to disqualification.
An exception from the above rule: if your submissions scores 0 / -1 / X / Fails, then you may make a new submission after a delay of 7 hours from your last submission timestamp. But you are only allowed to do this once a day. We have seen in the past that due to TC systems still scoring in background, competitors tends to think that submission has failed, and they keep submitting multiple times choking our submission queue and also adding duplicate submissions in queue. This is to avoid such scenarios and since each submission can take a long time to be processed on our systems, we need to ensure that TC systems are not unnecessary burdened.
To allow you to use whatever language and tools you are familiar with, we are asking to provide a Docker container that will read in the input files and write out the output files in mounted folders. So you can use whatever you want inside this Docker, we only ask you to make sure to respect the input and output format.
More precisely, this container has to have an entrypoint that will read in two command-line arguments: the location of the input file and the location of the output folder. To make your life easier, we provide examples of Dockerfiles (and associated entrypoints) for all of the example submissions. Make sure to specify the entrypoint using the JSON notation, with square brackets, as is shown in the examples.
The input file is an HDF5 file, which contains a matrix: the counts (/data/counts). This matrix contains the expression of genes (columns) within hundreds to millions of cells (rows). Example HDF5 files are present in the examples inputs folder (dataset.h5).
Because the data is very sparse, the matrix is stored inside a sparse and memory efficient format: Compressed Sparse Column format (CSC). For an example of how to read in these matrices, refer to the example submissions. This format stores three sparse array, i, p and x. This is a column-oriented format, in which x contains the actual values, i contains the row index for each value, and p points to column starts in i and x (i.e. pj until pj+1 are the values from x and i that are in column j). For example:
p = [0, 1, 3, 6]
i = [0, 0, 1, 0, 1, 2]
x = [11, 22, 33, 44, 55, 66]
Produces the matrix:
11 22 44
33 55
66
We also provide rownames with unique cell identifiers, and dims with the dimensions of the matrix, i.e. how many cells and how many genes we need to analyze.
Your solution should output two comma separated files:
Example milestone_network.csv:
from,to,length
A,B,1
Example progressions.csv (first 10 rows):
cell_id,percentage,from,to
C1,0.2304303,A,B
C2,0.1537403,A,B
C3,0.9627531,A,B
C4,0.0811708,A,B
C5,0.2478125,A,B
C6,0.3013250,A,B
C7,0.2876437,A,B
C8,0.1923322,A,B
C9,0.1827381,A,B
C10,0.1598463,A,B
The example submissions also demonstrate how to save these two objects.
The majority of examples are considered “normal” size, and are available in the public training data folder. Two others are considered extra-large, and have been pulled aside into a big-train folder for clarity. Can your solution scale?

network1 <- datasets$bifurcating %>%
simplify_trajectory() %>%
.$milestone_network
network2 <- datasets$bifurcating2 %>%
simplify_trajectory() %>%
.$milestone_network
dyneval::calculate_him(network1, network2)
## HIM
## 0.9233855

It then calculates two scores. The Recovery assesses how well each branch within the gold standard has a similar branch in the prediction:

The Relevance assesses how well each branch within the prediction has a similar branch in the gold standard:

The final score (F1branches) is then the harmonic mean between the Recovery and Relevance. A harmonic mean is used here to make sure that both the Relevance and Recovery are high. If either score is low, the harmonic mean will also be low. In the worst case, if either component is zero, the harmonic mean is also zero.

If a cell has a similar position in both the ground truth trajectory as in a predicted trajectory, it’s distance should also be relatively similar to other cells. To calculate the similarity between the relative positions of cells, we therefore calculate the Spearman’s correlation between all pairwise geodesic distances. Because we calculate a correlation, the absolute magnitude in the geodesic distances doesn’t matter, but rather the distance relative to all other distances.
baseline = 10 + 0.01 * cells
There is no limit on per-case run time, but there is an overall limit of 5 hours to process all 80 provisional cases. This is enough to take twice as long as the baseline timing, plus some margin for error and system overhead.
# download the datasets and put them inside the datasets/training/ folder
# build the method container
CONTAINER_FOLDER=containers/tc-submissions/submission-r/code
IMAGE=dynverse/python_example
chmod +x $CONTAINER_FOLDER/main.py
docker build -t $IMAGE $CONTAINER_FOLDER
# create a folder to store the output and scores
OUTPUT_FOLDER=$(pwd)/results
OUTPUT_MOUNT="-v $OUTPUT_FOLDER:/outputs/"
mkdir $OUTPUT_FOLDER
# define the folders where the data is stored
DATA_FOLDER=$(pwd)/datasets/training/
DATA_MOUNT="-v $DATA_FOLDER:/data/"
# run on one dataset --------------------------------------------
# this uses the default entrypoint
DATASET_ID=real-gold-aging-hsc-old_kowalczyk
mkdir $OUTPUT_FOLDER/$DATASET_ID
/usr/bin/time -o $OUTPUT_FOLDER/$DATASET_ID/time.txt -f "%e" \
docker run $DATA_MOUNT $OUTPUT_MOUNT $IMAGE \
/data/inputs/${DATASET_ID}.h5 /outputs/${DATASET_ID}/
ls $OUTPUT_FOLDER/$DATASET_ID
# run on many datasets ------------------------------------------
# this uses the runner script (scripts/runner.sh)
sh scripts/runner.sh $DATA_FOLDER $OUTPUT_FOLDER $IMAGE
# then evaluate it using the dyneval docker
docker run $DATA_MOUNT $OUTPUT_MOUNT dynverse/tc-scorer:0.3
# the overall score is present in ...
cat $OUTPUT_FOLDER/AGGREGATED_SCORE
# the scores on each dataset can be viewed in
head $OUTPUT_FOLDER/dataset_scores.csv
You can get an overview of the estimated difficulty of a dataset in difficulties.csv. The mean column gives you the difficulty rating for each component of the score (the lower the more difficult), while sd gives the standard deviation, which affects how much a deviation from the average will impact scoring. One factor in the difficulty is the kind of trajectory topology: linear and bifurcating datasets are often easier than graph or tree datasets.
Concepts and limitations for learning developmental trajectories from single cell genomics (2019): A review on trajectory inference algorithms
However, as an additional step, the training process will also be verified to make sure that your results are reproducible using only the data sources that are allowed as training data. Note that this step will not be done during the submission phase, so you should take extra care in testing that your training process runs error free. In case either we can not reproduce or complete this step, you might not qualify for a prize.
If that doesn't help, please do report the issue to support@topcoder.com and we will make sure the registration succeeds.
Preregistration Start Date: 7th June, 2019
Challenge Launch / Live Date: 21st Dec, 2019
Challenge Prizes: $8,000 / $6,000 / $4,000 / $2,000 / $1,000 / $750 / $750 / $500 / $500 / $500
Introduction and biological background
Our body is comprised of trillions of cells with different functions and programs, and their characterization is an exciting and open scientific question.Recent technological progress has allowed us to measure the current state of a cell. In this competition we focus on the transcriptome of a cell (i.e. the expression of the genes), which can be analyzed with single-cell RNA-sequencing technologies. In recent years these techniques have scaled up to being able to assess the expression (i.e. activity) of thousands of genes within tens of thousands of cells.
The state of a cell often changes gradually, and so does its transcriptome. In fact, cells are constantly changing based on external and internal stimuli. These can include:
- Cell differentiation, a process where cells go from a more stem-cell like state to a specialized state.
- Cell division, a process where cells replicate their DNA and split into two new cells.
- Cell activation, a process where cells are activated by their environment and react to it.
The topology of a trajectory can range from very simple (linear or circular) to very complex (trees or disconnected graphs).
Problem description and task overview
You are given the expression of thousands of genes within thousands of cells. This expression is given as a counts matrix, indicating how often a particular gene was counted within a cell. The goal is to construct a topology that represents these cells, and to place these cells on the correct locations along this topology. The basic idea is that cells that have similar expression should be closer in space. You can think of a cell as a vector in a N-dimensional space, the component of this vector are the genes and the values the gene expression. In this way it is possible to define formally a distance/similarity between cells. The big picture is: how can we order and organize the cells into a topology that captures their potential paths across a biological process?The topology is a graph structure, in this context called the milestone network as it connects “milestones” that cells pass through. Each edge within the milestone network can only be present once, and every edge has an associated length, which indicates how much the gene expression has changed between two milestones.
The cells are placed at a particular position of this milestone network. We represent this as “progressions”, where each cell is assigned to an edge and a percentage indicating how far it has progressed in that edge.
Quick start
To get started, we have provided example submissions in a few different programming languages. These examples infer a simple linear trajectory by using the first component of a principal component analysis as progression. See the forum for detailed information about these examples.Detailed description and submission format
This match uses the "submit code" submission style. The required format of the submission package is specified in a submission template document. This current document gives only requirements that are either additional or override the requirements listed in the template.You must not submit more often than 2 times a day. The submission platform does not enforce this limitation, it is your responsibility to be compliant to this limitation. Not observing this rule may lead to disqualification.
An exception from the above rule: if your submissions scores 0 / -1 / X / Fails, then you may make a new submission after a delay of 7 hours from your last submission timestamp. But you are only allowed to do this once a day. We have seen in the past that due to TC systems still scoring in background, competitors tends to think that submission has failed, and they keep submitting multiple times choking our submission queue and also adding duplicate submissions in queue. This is to avoid such scenarios and since each submission can take a long time to be processed on our systems, we need to ensure that TC systems are not unnecessary burdened.
To allow you to use whatever language and tools you are familiar with, we are asking to provide a Docker container that will read in the input files and write out the output files in mounted folders. So you can use whatever you want inside this Docker, we only ask you to make sure to respect the input and output format.
More precisely, this container has to have an entrypoint that will read in two command-line arguments: the location of the input file and the location of the output folder. To make your life easier, we provide examples of Dockerfiles (and associated entrypoints) for all of the example submissions. Make sure to specify the entrypoint using the JSON notation, with square brackets, as is shown in the examples.
The input file is an HDF5 file, which contains a matrix: the counts (/data/counts). This matrix contains the expression of genes (columns) within hundreds to millions of cells (rows). Example HDF5 files are present in the examples inputs folder (dataset.h5).
Because the data is very sparse, the matrix is stored inside a sparse and memory efficient format: Compressed Sparse Column format (CSC). For an example of how to read in these matrices, refer to the example submissions. This format stores three sparse array, i, p and x. This is a column-oriented format, in which x contains the actual values, i contains the row index for each value, and p points to column starts in i and x (i.e. pj until pj+1 are the values from x and i that are in column j). For example:
p = [0, 1, 3, 6]
i = [0, 0, 1, 0, 1, 2]
x = [11, 22, 33, 44, 55, 66]
Produces the matrix:
11 22 44
33 55
66
We also provide rownames with unique cell identifiers, and dims with the dimensions of the matrix, i.e. how many cells and how many genes we need to analyze.
Your solution should output two comma separated files:
- The milestone_network.csv is a table containing how milestones are connected (from and to) and the lengths of these connections (length).
- The progressions.csv contains for each cell (cell_id) where it is located along this topology (from, to, and a percentage in [0, 1]).
Example milestone_network.csv:
from,to,length
A,B,1
Example progressions.csv (first 10 rows):
cell_id,percentage,from,to
C1,0.2304303,A,B
C2,0.1537403,A,B
C3,0.9627531,A,B
C4,0.0811708,A,B
C5,0.2478125,A,B
C6,0.3013250,A,B
C7,0.2876437,A,B
C8,0.1923322,A,B
C9,0.1827381,A,B
C10,0.1598463,A,B
The example submissions also demonstrate how to save these two objects.
Training data
In addition to the example inputs and outputs, there is a large sample of additional cases on which to train or tune your approaches. These are designed to cover the full range of trajectories and data scales from the provisional and final test cases, but they are not necessarily drawn from the same pools of data originally.The majority of examples are considered “normal” size, and are available in the public training data folder. Two others are considered extra-large, and have been pulled aside into a big-train folder for clarity. Can your solution scale?
Code requirements
- Your code must process the test cases independently from each other. When processing a test case you MUST NOT read data from any other folder than those specified in the corresponding parameters files, and those folders that are already part of your submission. Breaking this rule is strictly against the rules and spirit of the contest and leads to immediate disqualification.
- The allowed time limit for the submission during provisional testing is 5 hours for 80 cases. The final test set may have a different number of cases or a different distribution of case sizes, but the overall time limit will be scaled according to the change in baseline times.
- There is no per-case time limit, but there is a run time scoring component.
- Your Docker image will be run on a high-memory Linux AWS r5.xlarge instance. Please refer to the AWS documentation for the details of this instance type.
- The Docker container for your solution will be run with a 24G memory limit.
Evaluation
Your output will be compared to the known (or expected) trajectory for a set of synthetic and real datasets with different topologies, cell or gene number, and increasing difficulty. This is done using four metrics, each contributing (on average) 1/4th to the overall score. In addition we provide some “baseline” methods already developed by the community, so you can have a sense of how far you are from the “best” methods. More detail about these baseline methods is available in the forums. Can you beat them?Similarity between the topologies
This l calculates a distance measures between two topologies. The score ignores any “in between” milestones, i.e. those with degree 2. It therefore does not matter whether you return a trajectory as a network A->B->C versus A->B. The order of the edges also doesn’t matter.network1 <- datasets$bifurcating %>%
simplify_trajectory() %>%
.$milestone_network
network2 <- datasets$bifurcating2 %>%
simplify_trajectory() %>%
.$milestone_network
dyneval::calculate_him(network1, network2)
## HIM
## 0.9233855
Similarity between the assignment of cells to particular branches
A branch is defined as a set of edges with no branching points, i.e. just a linear progression from one milestone to another milestone. This metric checks whether each branch with the gold standard can be mapped to a similar branch in the predicted trajectory, and vice versa. It does this by first calculating the number of overlapping cells between each pair of branches using a Jaccard score:It then calculates two scores. The Recovery assesses how well each branch within the gold standard has a similar branch in the prediction:
The Relevance assesses how well each branch within the prediction has a similar branch in the gold standard:
The final score (F1branches) is then the harmonic mean between the Recovery and Relevance. A harmonic mean is used here to make sure that both the Relevance and Recovery are high. If either score is low, the harmonic mean will also be low. In the worst case, if either component is zero, the harmonic mean is also zero.
Similarity between relative positions of cells within the trajectory
To determine whether cells have similar positions in the trajectory, we first calculate the geodesic distances between every pair of cells. The geodesic distance is defined as the shortest distance between two cells by following the edges within the trajectories. The lengths of the edges are taken into account in this calculation, but not the direction. This distance is illustrated in the following figure:If a cell has a similar position in both the ground truth trajectory as in a predicted trajectory, it’s distance should also be relatively similar to other cells. To calculate the similarity between the relative positions of cells, we therefore calculate the Spearman’s correlation between all pairwise geodesic distances. Because we calculate a correlation, the absolute magnitude in the geodesic distances doesn’t matter, but rather the distance relative to all other distances.
Running time
The per-case running time in seconds is compared to a baseline time. If the case runs as fast as the baseline or faster, the time score is 1. Otherwise, the score decreases to 0 as baseline / time, e.g. running twice as long as the baseline will score as 0.5. The baseline is computed based on the number of cells in the test case, plus some time for setup, as:baseline = 10 + 0.01 * cells
There is no limit on per-case run time, but there is an overall limit of 5 hours to process all 80 provisional cases. This is enough to take twice as long as the baseline timing, plus some margin for error and system overhead.
Score aggregation
The metrics are aggregated for each dataset using a geometric mean. That means that low values (i.e. close to zero) for any of the metrics results in a low score overall. They are also weighted so that:- A slight difference in performance for more difficult datasets is more important than an equally slight difference for an easy dataset.
- Datasets with a more rare trajectory type (e.g. tree) are given relatively more weight than frequent topologies (e.g. linear).
Evaluating a method locally
You can run a method and the evaluation locally using the script scripts/example.sh:# download the datasets and put them inside the datasets/training/ folder
# build the method container
CONTAINER_FOLDER=containers/tc-submissions/submission-r/code
IMAGE=dynverse/python_example
chmod +x $CONTAINER_FOLDER/main.py
docker build -t $IMAGE $CONTAINER_FOLDER
# create a folder to store the output and scores
OUTPUT_FOLDER=$(pwd)/results
OUTPUT_MOUNT="-v $OUTPUT_FOLDER:/outputs/"
mkdir $OUTPUT_FOLDER
# define the folders where the data is stored
DATA_FOLDER=$(pwd)/datasets/training/
DATA_MOUNT="-v $DATA_FOLDER:/data/"
# run on one dataset --------------------------------------------
# this uses the default entrypoint
DATASET_ID=real-gold-aging-hsc-old_kowalczyk
mkdir $OUTPUT_FOLDER/$DATASET_ID
/usr/bin/time -o $OUTPUT_FOLDER/$DATASET_ID/time.txt -f "%e" \
docker run $DATA_MOUNT $OUTPUT_MOUNT $IMAGE \
/data/inputs/${DATASET_ID}.h5 /outputs/${DATASET_ID}/
ls $OUTPUT_FOLDER/$DATASET_ID
# run on many datasets ------------------------------------------
# this uses the runner script (scripts/runner.sh)
sh scripts/runner.sh $DATA_FOLDER $OUTPUT_FOLDER $IMAGE
# then evaluate it using the dyneval docker
docker run $DATA_MOUNT $OUTPUT_MOUNT dynverse/tc-scorer:0.3
# the overall score is present in ...
cat $OUTPUT_FOLDER/AGGREGATED_SCORE
# the scores on each dataset can be viewed in
head $OUTPUT_FOLDER/dataset_scores.csv
Additional information
Normalization of datasets
Single-cell RNA-seq datasets are often normalized so that the expression of different cells is more comparable. This can involve:- Dividing the counts of each cell by the total number of counts per cell.
- Log2 normalisation.
- Many more complex approaches that are available in packages such as scran (R/Bioconductor), sctransform (R) and scanpy (Python).
Difficulty of datasets
There is a broad gradient of difficulty among the datasets. Some datasets could be solved by pen and paper, while others may almost be impossible to correctly define the trajectory. Don’t try to optimise a method for all datasets, but rather try to learn from datasets that are next in your “difficulty” frontier.You can get an overview of the estimated difficulty of a dataset in difficulties.csv. The mean column gives you the difficulty rating for each component of the score (the lower the more difficult), while sd gives the standard deviation, which affects how much a deviation from the average will impact scoring. One factor in the difficulty is the kind of trajectory topology: linear and bifurcating datasets are often easier than graph or tree datasets.
Further reading
A comparison of single-cell trajectory inference methods (2019): Benchmarking study of current state-of-the-art methods for trajectory inference. https://doi.org/10.1038/s41587-019-0071-9Concepts and limitations for learning developmental trajectories from single cell genomics (2019): A review on trajectory inference algorithms
Final testing
Because of the "submit code" style used in this match there are no significant differences between provisional and final testing of your solution quality. During final testing your code will be executed on sequestered data that were not used in the provisional testing phase. The test set may have a different number of cases or a different distribution of case sizes, but the overall time limit will be scaled according to the change in baseline times.However, as an additional step, the training process will also be verified to make sure that your results are reproducible using only the data sources that are allowed as training data. Note that this step will not be done during the submission phase, so you should take extra care in testing that your training process runs error free. In case either we can not reproduce or complete this step, you might not qualify for a prize.
General notes
- This match is rated.
- Relinquish - Topcoder is allowing registered competitors to "relinquish". Relinquishing means the member will compete, and we will score their solution, but they will not be eligible for a prize. Once a competitor relinquishes, we post their name to a forum thread labeled "Relinquished Competitors".
- Use the match forum to ask general questions or report problems, but please do not post comments and questions that reveal information about the problem itself or possible solution techniques.
- The goal of this competition is to improve the status quo of current methods for trajectory reconstruction. Therefore exact copies of solutions that were created before the contest launch, or reimplementation with minimal adaptations, are accepted but are not eligible for prizes. If you plan to make such submission for testing purposes, please let us know so that you can be relinquished. In order to be prize-eligible, you must contribute in a substantial way to the effectiveness of the solution, and that contribution must have been created during the contest live period.
- In this match you may use any programming language and libraries, including commercial solutions, provided Topcoder is able to run it free of any charge. You may also use open source languages and libraries, with the restrictions listed in the next section below. If your solution requires licenses, you must have these licenses and be able to legally install them in a testing VM (see “Requirements to Win a Prize” section). Submissions will be deleted/destroyed after they are confirmed. Topcoder will not purchase licenses to run your code. Prior to submission, please make absolutely sure your submission can be run by Topcoder free of cost, and with all necessary licenses pre-installed in your solution. Topcoder is not required to contact submitters for additional instructions if the code does not run. If we are unable to run your solution due to license problems, including any requirement to download a license, your submission might be rejected. Be sure to contact us right away if you have concerns about this requirement.
- You may use open source languages and libraries provided they are equally free for your use, use by another competitor, or use by the client. If your solution includes licensed elements (software, data, programming language, etc) make sure that all such elements are covered by licenses that explicitly allow commercial use.
- If your solution includes licensed software (e.g. commercial software, open source software, etc), you must include the full license agreements with your submission. Include your licenses in a folder labeled “Licenses”. Within the same folder, include a text file labeled “README” that explains the purpose of each licensed software package as it is used in your solution.
Final prizes
In order to receive a final prize, you must do all the following:- Achieve a score in the top twenty according to final system test results. See the "Scoring" and "Final testing" sections above.
- Once the final scores are posted and winners are announced, the prize winner candidates have 7 days to submit a report outlining their final algorithm explaining the logic behind and steps to its approach. You will receive a template that helps create your final report.
- If you place in a prize winning rank but fail to do any of the above, then you will not receive a prize, and it will be awarded to the contestant with the next best performance who did all of the above.
Ownership rights of submissions
Winning submissions will be open sourced. Please assign an Apache2 license for your submission to be considered for the prize. Challenge submissions must contain the following open source license: Apache-2.0. Submissions without this license will not be considered for placement. The license file must exist at the base or the root of the submission file tree structure. The license file must be names LICENSE with all caps. It may have a txt extension or an md extension.Issues with registration
If you are a new user, and you get a failure while trying to register that asks you to contact support, you are always welcome to do so. But this issue can often be resolved more quickly by refreshing the page or restarting the browser.If that doesn't help, please do report the issue to support@topcoder.com and we will make sure the registration succeeds.