February 4, 2022

Print all Subset for set (Backtracking and Bitmasking approach)

Kulwinder Kaurkulwinder3213

DURATION

11min

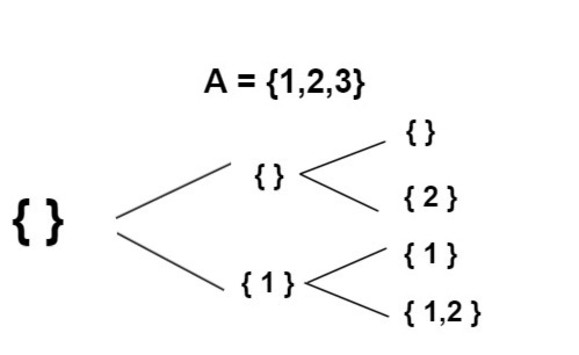
Backtracking Approach

In this approach we make a call to subsetBacktrack() to find subsets. For each element we have two choices, either to take in a subset or not. We will call the recursive method based on these choices.

Algorithm

Step 1: Call will be made to subsetBacktrack() with S as array of integers, list for storing and printing subset, and i index.

Step 2: If all the elements of the array are processed then print list and return from method.

Step 3: Two Choices - include the current element into the subset. If yes then add current element to list and call subsetBacktrack with i++. Otherwise call method subsetBacktrack with the same arguments.

Step 4: Print all the subsets.

Pseudo Code

1
2
3
4
5
6
7
8
9
10
11
12
13
int arr[N]
void allSubsets(int pos, int len, int[] subset) {
  if (pos == N) //position
  {
    print(subset)
    return
  }
  subset[len] = arr[pos]
  //take element
  allSubsets(pos + 1, len + 1, subset)
  // Skip the current element.
  allSubsets(pos + 1, len, subset)
}

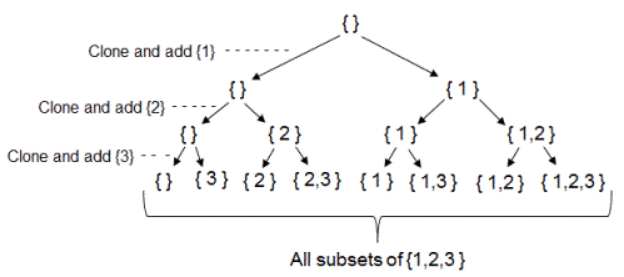
Java Implementation

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
import java.util.*;
import java.lang.*;

class Solution {

  public static ArrayList < ArrayList < Integer >> subsets(int[] nums) {
    ArrayList < Integer > curr = new ArrayList < Integer > ();
    ArrayList < ArrayList < Integer >> ans = new ArrayList < ArrayList < Integer >> ();
    find_subset(nums, 0, curr, ans);
    return ans;
  }

  public static void find_subset(int[] nums, int i, ArrayList < Integer > curr, ArrayList < ArrayList < Integer >> ans) {
    if (i == nums.length) {
      ans.add(new ArrayList(curr));
      return;
    }
    curr.add(nums[i]);
    find_subset(nums, i + 1, curr, ans);
    curr.remove(curr.size() - 1);
    find_subset(nums, i + 1, curr, ans);
  }
  public static void main(String args[]) {
    int arr[] = {
      1,
      2,
      3,
      4
    };

    ArrayList < ArrayList < Integer >> list = subsets(arr);

    for (int ii = 0; ii < list.size(); ii++) {
      ArrayList < Integer > ls = list.get(ii);
      System.out.print("{");
      for (Integer k: ls) {
        System.out.print(k + " ");
      }
      System.out.println("}");
    }

  }
}

Complexity Analysis

Time Complexity: O (N(2^N))
For every element there will be two cases, so O (2^N) and time taken to copy N elements.

Space Complexity: O(N)
We have used extra space to store all elements for subsets.

Output Snippet
{1 2 3 4 }
{1 2 3 }
{1 2 4 }
{1 2 }
{1 3 4 }
{1 3 }
{1 4 }
{1 }
{2 3 4 }
{2 3 }
{2 4 }
{2 }
{3 4 }
{3 }
{4 }
{}

Code Output Snippet

Bitmasking Approach

In bitmasking, each element of an array represents a bit. For each element present at ith location the bit will be 0 or 1, that is, ith entry will be either true or false. Using iteration we will generate a truth table and for each entry generated a subset with its elements will be decided.

Algorithm

Step 1: SubSet() method will be called passing arr and size N.

Step 2: Calculate size, which is 2^N, because there are 2^N subsets present for a set with N length.

Step 3: Loop 0 to 2^N (i).

Step 4: Inner loop 0 to N (j), create string or list to store subset elements, calculate bit for each element of an array. If the ith bit in the index set is 1 then add to list as a subset element.

Pseudo Code

1
2
3
4
5
6
7
8
9
10
11
12
13
subSet(int arr[], int n) {
  int subset_size = pow(2, n) //total 2^n subsets
  int index, i
  //truth table 000..0 to 111..1
  for (index from 0 to subset_size) {
    int subset[n]
    for (i from 0 to n) {
      if (index & (1 << i))
        subset[i] = S[i]
    }
    print(subset)
  }
}

Java Implementation

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
import java.io.*;
import java.util.*;
import java.lang.*;
public class Solution {
  static void subSet(int arr[], int N) {

    List < String > list = new ArrayList < > ();
    int size = (int) Math.pow((double) 2, (double) N);
    System.out.println("size" + size);
    for (int i = 0; i < size; i++) {
      String s = "";
      for (int j = 0; j < N; j++) {
        if ((i & (1 << j)) > 0)
          s += arr[j] + " ";
      }

      if (!(list.contains(s))) {
        list.add(s);
      }
    }

    for (int ii = 0; ii < list.size(); ii++) {
      String s = list.get(ii);

      String str[] = s.split(" ");
      System.out.print("{ ");
      for (int jj = 0; jj < str.length; jj++) {
        if (ii == 0)
          System.out.print(str[jj])
        else
          System.out.print(Integer.parseInt(str[jj]) + " ");
      }
      System.out.print(" }\n");
    }
  }

  public static void main(String[] args) {
    Scanner sc = new Scanner(System.in);

    int N = 3;
    int arr[] = {
      10,
      12,
      12
    };
    subSet(arr, N);

  }
}