Intersection of Two LinkedLists

Suppose we are given two LinkedLists, L1 and L2. Both meet at a certain node and we need to find whether both the LinkedLists intersect. If yes, then we need to return the node at which both the LinkedLists meet.

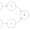
In the above figure we can see that the last node of L1 is pointing to the node of L2 instead of pointing to NULL.
We will use different methods to find the intersection of L1 and L2.
Let’s understand LinkedList intersections using a different case.

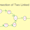
In the above picture there are i and j different LinkedLists which end at point E. The LinkedList J which should have an end point A, but rather than pointing to A it points to the node having data 4 of linked list i. So the point is to calculate the node where both the LinkedLists are going to intersect. In this case it is the node having data 4, which is the common node for both the LinkedLists.

Brute Force Approach (Two Loops)

In this approach we will take a node of L1 and we will check if the current node is present in List L2.

Let’s use the above example to understand the brute force approach for LinkedList intersection:
In this case we will take a1-> a2-> c1->c2->c3 as a different LinkedList and we will check the existence of each node in a second linked list, which is b1->b2->b3->c1->c2->c3.

Now for each node of the first LinkedList we need to iterate over the second LinkedList, then we will use two iterations for finding the intersection point.

Java Implementation

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
**
*
Definition
for singly - linked list.*public class ListNode {
    * int val;
    * ListNode next;
    * ListNode(int x) {
        * val = x;
        * next = null;
        *
      }
      *
  }
  */
public class Solution {
  public ListNode getIntNodeMethod(ListNode headA, ListNode headB) {

    ListNode currA = headA;
    ListNode currB = headB;

    ListNode res = null;

    while (currA != null) {
      currB = headB;
      while (currB != null) {
        if (currA == currB) {
          return currA;
        }

        currB = currB.next;
      }
      currA = currA.next;
    }
    return res;
  }
}

Code snippet

Using DataStructure Technique

Finding the intersection using hashing will help us to find the intersection node only in O(N) time complexity. We will create a hashset and insert all the nodes from L1. Then we will traverse L2 and using hashing we will check if the current node of L2 is present. This will improve complexity from O(N*N) and the space complexity will be O(N). When we find the node which is already present in our hashset then we will return the node, otherwise after traversing L2 we will return null node.

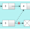
Above is the example for intersecting LinkedLists.

The above figure shows how the hashing concept will be used. There are buckets present and when we try to add a node which is already present, we will check in code using O(1) time complexity whether the current node is already present or not. When the case comes in which the current node is already present, then it is the required node.

The main idea of using the hashing concept is to reduce the time complexity as hash code for each node will be different, so using a new hashset will help to reduce the same complexity from O (N*N).

Java Implementation

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for singly-linked list.
 * public class ListNode {
 * 	int val;
 * 	ListNode next;
 * 	ListNode(int x) {
 *     	val = x;
 *     	next = null;
 * 	}
 * }
 */
public class SolutionClass {
  public ListNode getIntNodeMethod(ListNode headA, ListNode headB) {

    HashSet < ListNode > map = new HashSet < > ();
    ListNode tmp = headA;

    while (tmp != null) {
      map.add(tmp);

      tmp = tmp.next;
    }

    tmp = headB;

    while (tmp != null) {
      if (map.contains(tmp)) return tmp;

      tmp = tmp.next;
    }

    return tmp;

  }
}

Code Snippets

Two Pointers Approach

In the hashing technique we have O(N) time complexity but there is a chance that we can improve the complexity of finding the intersection by O(1). This can be achieved by taking two pointers. Pointer1 will point to the head of L1 and pointer2 will point to the head of L2. The solution is that the intersection of the LinkedLists to the end of LinkedLists will be common, as the tail will be common in both LinkedLists. So we will keep checking until pointer1 is not equal to pointer2.

Algorithm

Method: getIntNodeMethod(headA, headB) will be called passing pointer or head of both LinkedLists.
pointer1, pointer2 will point to headA and headB respectively.
Loop → Run until pointer1 != pointer2

• if pointer1 is equal to null, set it as headB
  else pointer1= pointer1.next

• if pointer2 is equal to null, set is as headA
  else pointer2= pointer2.next
  Return the pointer2

Java Implementation

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class SolutionClass {
  public ListNode getIntNodeMethod(ListNode headA, ListNode headB) {

    ListNode pointer1 = headA;
    ListNode pointer2 = headB;

    while ((pointer1 != pointer2)) {

      pointer1 = pointer1.next;
      pointer2 = pointer2.next;

      if (pointer1 == null)
        pointer1 = headB;
      if (pointer2 == null)
        pointer2 = headA;

    }
    return pointer1;

  }
}

Code Snippet