July 10, 2012
SRM 549

DURATION
25 mincategories
Tags
share
Match Summary
Round Overview
Discuss this match
This SRM is the debut for tehqin as a writer and me as an Editorial Writer. Most of the problems were themed around magical objects. In division 1, tourist won the match convincingly, being the only coder to have successfully solved all three problems. He was followed by wata and Petr. Division 2 was won by elfus, followed by Caiych and newcomer LvSakura. In division 2, no one could solve all three problems.
Used as: Division Two - Level One:
| Value | 250 |
| Submission Rate | 639 / 712 (89.75%) |
| Success Rate | 497 / 639 (77.78%) |
| High Score | experience257 for 246.39 points (3 mins 26 secs) |
| Average Score | 183.66 (for 497 correct submissions) |
Let’s solve the problem by breaking it down into smaller cases:
If numSwaps is zero, then the ball stays where it was initially. Otherwise:
If the ball is initially at spot 1 (i.e. the middle spot) then:
An even number of swaps will bring it back to spot 1. So we should return 1 as an answer in this case.
an odd number swaps will take it to either spot 0 or spot 2 with equal probability. The probability are equal because any move that moves the ball from spot 1 to spot 2 can be replaced with a move that moves it to spot 0 or vice versa. So in this case the answer should be 0.
If the ball is at spot 0 or spot 2 then the first swap will take it to the spot 1 and it boils down to Case 2, which we have solved already.
Here is a simple implementation:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int getHat(string hats, int numSwaps) {
int initSpot;
for (int i = 0; i < 3; ++i) {
if (hats[i] == 'o')
initSpot = i;
}
if (numSwaps == 0)
return initSpot;
// if the ball it in spot 0 or spot 2, perform a single swap to move it to spot 1.
if (initSpot != 1) {
--numSwaps;
initSpot = 1;
}
if (numSwaps % 2 == 0)
return 1;
else
return 0;
}
Alternative solutions and additional comments.
Recursive Solution:
1
2
3
4
5
6
7
8
9
10
11
12
class BallAndHats {
public: int rec(int pos, int nS) {
if (nS == 0)
return pos;
if (pos >= 2)
return rec(pos - 1, nS - 1);
return (pos + (nS % 2)) % 2;
}
int getHat(string hats, int numSwaps) {
return rec(hats.find("o"), numSwaps);
}
};
PointyWizardHats
Problem Details
Used as: Division Two - Level Two:
| Value | 500 |
| Submission Rate | 202 / 712 (28.37%) |
| Success Rate | 60 / 202 (29.70%) |
| High Score | YuLiangyi for 414.95 points (13 mins 26 secs) |
| Average Score | 264.65 (for 60 correct submissions) |
Used as: Division One - Level One:
| Value | 250 |
| Submission Rate | 510 / 575 (88.70%) |
| Success Rate | 370 / 510 (72.55%) |
| High Score | hnu0314 for 248.47 points (2 mins 14 secs) |
| Average Score | 164.91 (for 370 correct submissions) |
An obvious simplification of the problem is to work with isosceles triangle instead of cones. We can rotate an isosceles triangle around its longest median to create a cone.
Lets answer the following question:
We are given a top cone with radius rT and height hT and a bottom cone with radius rB and height hB. How to determine if we can create a valid wizard hat using them ?
Observation: rB must be strictly greater than rT.
Proof: Assume that rB ≤ rT. Then the only way some part of the bottom cone will be visible is, if the apex of the cones touches each other and the height of the bottom cone is larger than that of the top cone(see figure 1 and 2) which is prohibited by the first condition.
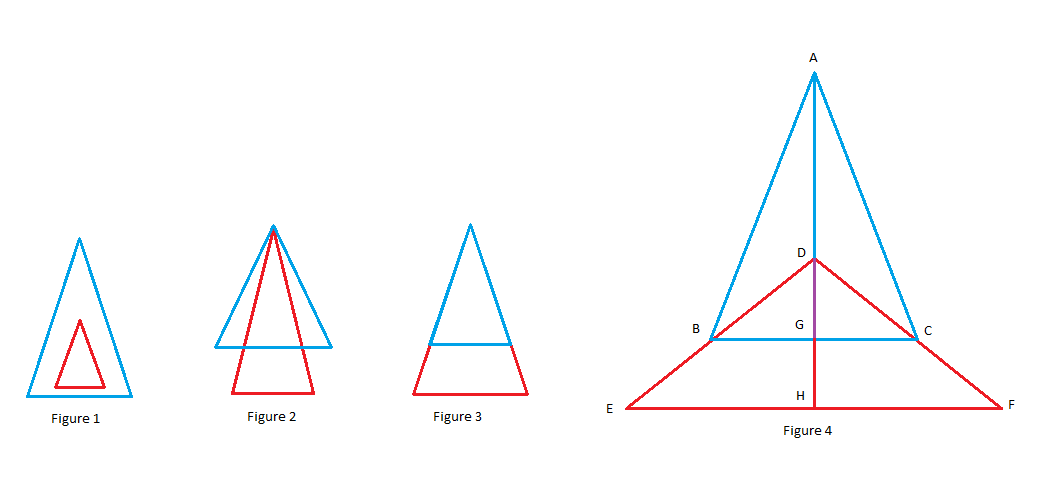
rB being greater than rT, is not enough for the construction of a valid hat. The apexes can still touch each other (see figure 3)
We shall need another condition to construct a valid hat and to obtain that condition, let’s look at a valid wizard hat on figure 4. Here, triangle ABC and DEF are isosceles triangles that represents the top cone and the bottom cone respectively.
Observation:
Triangle DBG and triangle DEH are similar triangles.
Proof:
Angle DGB = Angle DHE (both are right angles)
Angle BDG is common to both triangles.
So, the remaining angles are also equal and thus DBG and DEF are similar triangles.
It follows that:
DG/BG = DH/EH
DG = (DH/EH)*BG
Note that, in a valid hat DG is strictly smaller than AG. Otherwise the two apexes will meet.
DG < AG
(DH/EH)*BG < AG
DH*BG < AG*EH
hB*rT < hT*rB [and this is the other condition that we are going to need]
Now that we can determine whether a pair of cones can form a valid wizard hat, let’s solve the actual problem of finding the maximum number of hats that can be produced using each cone at most once.
Most of the coders seem to have identified this as a standard exercise of Bipartite Matching:
Build a bipartite graph with top hats on the left and bottom hats on the right
There is an edge between topHat[i] to bottomHat[j] if topHat[i] can be placed on top of bottomHat[j] to create a valid wizard hat.
The maximum bipartite matching in this graph is the desired answer. (Each edge of the matching would represent a single hat).
The following code implements this idea:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
bool graph[55][55];
int topN, bottomN;
int leftOf[55]; // leftOf[v] is a vertex on the left that was matched with vertex v on right
bool canPlace(int hT, int rT, int hB, int rB) {
return (rB > rT) && ((hT * rB) > (hB * rT));
}
bool seenL[55], seenR[55];
// this method searches for an alternating path to improve the current matching
bool bpm(int u) {
if (seenL[u])
return false;
seenL[u] = 1;
for (int v = 0; v < bottomN; ++v) {
if (graph[u][v] && !seenR[v]) {
seenR[v] = 1;
if (leftOf[v] == -1 || bpm(leftOf[v])) {
leftOf[v] = u;
return true;
}
}
}
return false;
}
int calc() {
memset(leftOf, -1, sizeof(leftOf));
int ret = 0;
int i;
for (i = 0; i < topN; ++i) {
memset(seenL, 0, sizeof(seenL));
memset(seenR, 0, sizeof(seenR));
if (bpm(i))
++ret;
}
return ret;
}
class PointyWizardHats {
public: int getNumHats(vector < int > topHeight, vector < int > topRadius, vector < int > bottomHeight, vector < int > bottomRadius) {
topN = topHeight.size();
bottomN = bottomHeight.size();
memset(graph, false, sizeof(graph));
int i, j;
// here we build the bipartite graph
// top hats are on the left and bottom hats are on the right
for (i = 0; i < topN; ++i) {
for (j = 0; j < bottomN; ++j) {
if (canPlace(topHeight[i], topRadius[i], bottomHeight[j], bottomRadius[j])) {
graph[i][j] = true;
}
}
}
return calc();
}
};
Used as: Division Two - Level Three:
| Value | 1000 |
| Submission Rate | 12 / 712 (1.69%) |
| Success Rate | 2 / 12 (16.67%) |
| High Score | elfus for 596.47 points (27 mins 40 secs) |
| Average Score | 520.71 (for 2 correct submissions) |
Let us define the problem in simple graph theoritic terms:
We are given a directed graph G with at most 20 vertices, which possibly has cycles.
We are allowed to perform two types of operation on it:
Select 2 vertices u and v such that there are no edges between them. Draw an edge from u to v.
Delete at existing edge.
The question is, what is the minimum number of operations one has to perform in order to obtain a new graph that is acyclic? (i.e. has no cycles)
A simple observation:
you never need to draw a new edge to make a graph acyclic. This is true because, a new edge never cancels an existing cycle. So the only operation we are concerned with is, deleting existing edges.
Now the problem can be restated as: For a given directed graph G, what is the minimum number of edges that has to be deleted to obtain an acyclic graph?
The reason that we want to convert the graph into an acyclic one is to be able to find a valid topological order of the vertices.
Observation:
If t = {t[0], t[1], … t[n-1]} is a valid topological order of the vertices where n is the number of vertices in G then for all (i ≤ j), there is no edge from vertex t[j] to vertex t[i]. This is obviously true because otherwise vertex t[j] couldn’t be placed after vertex t[i] to form a valid topological order.
For any given possibly invalid topological order t, we can delete all edges (t[a], t[b]) such that b ≤ a. This will convert the invalid topological order into a valid one.
Lets call these unwanted edges: reverse edge
Claim:
If there exists a permutation T of the vertices of a graph G such that there are no reverse edges for T, then G is acyclic.
Proof:
This is obviously true because, in this case T represents a valid topological order of the vertices of G and only acyclic graphs can have valid topological order.
We can redefine our problem as:
Calculate the permutation of the vertices of the graph G that has the minimum number of reverse edges.
This can be solved by dynamic programming using the standard bitmask technique.
The number of vertices in the graph is at most 20. We can represent any subset of these vertices using the 20 least significant bits of an integer. The solution will explore at most 220 states. We shall need an array of size 220, which is reasonable.
I hope you will find the following code well-explained:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
int n, adjMask[22];
int dp[1 << 20];
const int INF = 1 << 29;
// returns true if the k-th least significant bit of mask is set to 1
bool isSet(int mask, int k) {
return (mask >> k) & 1;
}
// returns the number of 1-bits in m
int bitCnt(int m) {
int ret = 0;
while (m > 0) {
ret += (m & 1);
m >>= 1;
}
return ret;
}
// F (mask) returns the minimum number of reverse edges that will be created to
// sort the vertices represented by the 0 bits of "mask"
// mask represents the subset of vertices that has been topologically sorted
// among themselves at the current call of F we select a new vertex to place
// after the previously sorted vertices (e.g. those that are represented by "mask")
// for the newly selected vertex we calculate how many reverse edges are created
// as a result of placing this vertex
int F(int mask) {
if (mask == ((1 << n) - 1)) { // this is the state where all bits are set to 1,
// which means we have sorted all the vertices
return 0;
}
int & ret = dp[mask];
if (ret > -1) return ret;
ret = INF;
for (int i = 0; i < n; ++i) {
if (!isSet(mask, i)) {
int nextMask = mask | (1 << i);
ret = min(ret, bitCnt(nextMask & adjMask[i]) + F(mask | (1 << i)));
// bitwise-AND of nextMask and adjMask[i] gives us the set of vertices
// that has reverse edge from vertex-i
}
}
return ret;
}
class OrderOfTheHats {
public: int minChanged(vector < string > spellChart) {
n = spellChart.size();
// the following loop calculates a bit mask for each vertex
// adjMask[i] represents the subset of vertices that has an edge from vertex i
for (int i = 0; i < n; ++i) {
adjMask[i] = 0;
for (int j = 0; j < n; ++j) {
if (spellChart[i][j] == 'Y') {
adjMask[i] |= (1 << j);
}
}
}
memset(dp, -1, sizeof(dp));
return F(0); // we call F with all the bits of mask set to 0, which
// means no vertices has been chosen yet.
}
};
Used as: Division One - Level Two:
| Value | 600 |
| Submission Rate | 38 / 575 (6.61%) |
| Success Rate | 18 / 38 (47.37%) |
| High Score | tourist for 430.34 points (19 mins 31 secs) |
| Average Score | 279.76 (for 18 correct submissions) |
Observation:
Whenever you get a coin, the magician will give you the coin with the smallest value among the remaining coins.
Proof:
With a perfect strategy we can only maximize the number of coins to win. The value of the coins are fully determined by the moves of the magician. So assuming that the magician knows that, we shall win k coins using our perfect strategy, he will make sure that we win the k smallest coins.
If we can calculate the maximum number of coins that can be won, we can calculate the maximum total value from that.
This can be done with dynamic programming. Note that, there can be at most 13 hats in the input grid. We do not need to consider other cells of the grid. At any moment in the game the hats can be in one of three different states:
State 0: The hat is not selected yet (by you)
State 1: The hat was selected and it contains a coin
State 2: The hat was selected but it is empty
We can represent the states of the game using ternary numbers (i.e. base 3 numbers). For example, assume that there are 3 hats in the grid. The first hat was selected and it contains a coin, the second hat is not selected yet and the third hat was selected and it was empty. We can represent this state of the game with the ternary number 102, which is 11 in decimal. There can be at most 313 = 1594323 different states which is not too big considering the fact that, not all states will be visited.
For a given state, we shall select a new hat that was not selected before and proceed. We shall use the first numGuesses selections for our guessing. The other selections will reveal hats but not be counted as guesses.
Few notes on the implementation:
it is good to treat ternary states like binary bitmasks. For that, we can write 2 simple methods setDigit() and checkDigit() that can change digit or read digit from any position of the ternary number using precomputed powers of 3.
we shall need some information frequently which can be computed from the ternary state. For example, the (number_of_coins + number_of_hats) for every row or column. Instead of calculating them from the ternary state, we can carry them along the recursive method for efficiency (see the code bellow).
The following C++ code implements this idea:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
#define NOT_SELECTED 0
#define HAS_COIN 1
#define NO_COIN 2
#define INFINITY 50
vector < pair < int, int > > hatPos;
vector < int > coins;
bool seen[2000000];
char dp[2000000];
int R, C, nHat, nCoin, numGuesses;
int pow3[15];
int setDigit(int state, int at, int newDigit) {
return (state / pow3[at + 1]) * pow3[at + 1] + newDigit * pow3[at] + state % pow3[at];
}
int checkDigit(int state, int at) {
return (state / pow3[at]) % 3;
}
// this method returns the maximum number of coins that we can win
// state - is a ternary (base 3) number representing the state of the hats
// all the other parameters in F are uniquely determined by the value of 'state'
// but calculating them at each step is costly, so we update and pass them with F as parameters
// rowCnt[r] keeps track of the total no. of hats and coins for row r
// colCnt[c] keeps track of the total no. of hats and coins for column c
int F(int state, int coinsPlaced, int hatsSelected, int rowCnt[], int colCnt[]) {
// this is the base case
// if the state is invalid we return -INFINITY
if (hatsSelected == hatPos.size()) {
if (coinsPlaced != coins.size()) // all the coin has to be placed
return -INFINITY;
for (int i = 0; i < R; ++i)
if (rowCnt[i] % 2 == 1) return -INFINITY; // for each row (number_of_hat + number_of_coins) must be even
for (int i = 0; i < C; ++i)
if (colCnt[i] % 2 == 1) return -INFINITY; // for each column (number_of_hat + number_of_coins) must be even
return 0;
}
int ret = dp[state];
if (seen[state])
return ret;
seen[state] = true;
ret = -INFINITY;
for (int i = 0; i < nHat; ++i) {
int r = hatPos[i].first, c = hatPos[i].second;
int d = checkDigit(state, i);
if (d == NOT_SELECTED) {
int res1 = -INFINITY, nextState;
if (coinsPlaced < coins.size()) {
// CASE 1: This hat has got a coin under it
int profit = 1;
if (hatsSelected >= numGuesses) // if no guesses are left, you can't have anymore coins
profit = 0;
nextState = setDigit(state, i, HAS_COIN);
rowCnt[r] += 2; // a coin under a hat increases rowCnt for row r by 2 [ the hat + the coin ]
colCnt[c] += 2; // similar thing happens for columns
res1 = profit + F(nextState, coinsPlaced + 1, hatsSelected + 1, rowCnt, colCnt);
rowCnt[r] -= 2;
colCnt[c] -= 2;
}
// CASE2: This hat has no coin under it
rowCnt[r]++; // only the hat is counted
colCnt[c]++;
nextState = setDigit(state, i, NO_COIN);
int res2 = F(nextState, coinsPlaced, hatsSelected + 1, rowCnt, colCnt);
rowCnt[r]--;
colCnt[c]--;
// we shall always try to go to valid states
if (res1 < 0) // if res1 is impossible, we compare only with res2
ret = max(ret, res2);
if (res2 < 0) // if res2 is impossible, we compare only with res1
ret = max(ret, res1);
else // if there are two choices, the magician will allow us the worse one
ret = max(ret, min(res1, res2));
}
}
return dp[state] = ret;
}
class MagicalHats {
public: int findMaximumReward(vector < string > board, vector < int > _coins, int _numGuesses) {
numGuesses = _numGuesses;
coins = _coins;
sort(coins.begin(), coins.end());
R = board.size();
C = board[0].size();
// the coordinates of the hats are stored.
for (int i = 0; i < R; ++i) {
for (int j = 0; j < C; ++j) {
if (board[i][j] == 'H') {
hatPos.push_back(make_pair(i, j));
}
}
}
nHat = hatPos.size();
nCoin = coins.size();
int rowCnt[15], colCnt[15];
for (int i = 0; i < R; ++i)
rowCnt[i] = 0;
for (int i = 0; i < C; ++i)
colCnt[i] = 0;
memset(seen, 0, sizeof(seen));
pow3[0] = 1;
for (int i = 1; i <= nHat; ++i)
pow3[i] = pow3[i - 1] * 3;
int coinCnt = F(0, 0, 0, rowCnt, colCnt);
if (coinCnt < 0) return -1;
int ret = 0;
for (int i = 0; i < coinCnt; ++i)
ret += coins[i];
return ret;
}
};
Used as: Division One - Level Three:
| Value | 950 |
| Submission Rate | 6 / 575 (1.04%) |
| Success Rate | 4 / 6 (66.67%) |
| High Score | tourist for 447.63 points (41 mins 41 secs) |
| Average Score | 432.02 (for 4 correct submissions) |
If you like implementation-heavy problems, this problem is for you!
One thing that immediately catches the eyes is that, the number of blocks will never be more than 6. This indicates to some brutal “brute-force”.
Let us understand the definition of “fundamentally different” clearly. The problem statement says:
Two structures built by Sophie are called fundamentally different if there are colors i and j such that in one structure there is at least one block of color i placed directly on top of a block of color j, and in the other structure there is no such pair of blocks.
Another way to look at this definition is:
For any given structure, we can build a graph having N vertices where N is the number of different types of blocks available. In this graph there is a directed edge from vertex u to vertex v if there is at least one block of color u on top of a block of color v in the given structure. For a strucure s, call this graph G(s). Two structures s1 and s2 are “fundamentally different” if and only if G(s1) and G(s2) are different.
If two structures are not “fundamentally different” we can call them “fundamentally equivalent”.
Denote by W(s) = the number of ways Josh can pick up the blocks of a structure s. Note that, for any two fundamentally equivalent structures s1 and s2, W(s1) = W(s2).
This is true because, at any move Josh can remove all the blocks of the same color C, such that, there are no blocks on top of any block of color C. So W(s) depends on G(s) and it can be calculated from G(s).
Denote by W(g), the number way Josh can pick up blocks from a structure s such that G(s) = g
An outline of a brute force solution:
Generate all possible graphs.
for each graph g:Check if g is a valid graph (i.e. there exists a structure s such that G(s) = g)
If g is valid, calculate W(g)
If W(g) is between the given limits minWays and maxWays, increase the desired answer by 1.
To generate all possible graphs, we can distribute the blocks among different heights in all possible ways (see the sample implementation for details).
Assuming that we have solved the problem of generating all possible graphs, we have 2 more sub problems to solve:
checking if the generated graph g is valid, and
calculating W(g)
Let’s define the validity checking problem clearly:
Given N types of blocks where blockTypes[i] is the number of blocks available of color i. Is it possible to build a structure s from these blocks such that G(s) = g?
This can be solved using maximum flow:
Construct a bipartite graph with N vertices on the left and N+1 vertices on the right. There is an edge from vertex u on the left to vertex v on the right if there is an edge from u to v in g (i.e. there exists a block of color u that is placed on top of a block of color v) The extra vertex on the right represents the ground, where the bottommost blocks are placed. The capacity of these edges will be infinity. We shall add a source and a sink. For each vertex u on the left, there will be an edge from source to u with capacity blockTypes[u]. Similarly for each vertex v on the right, there will an edge from v to sink with capacity blockTypes[v]. Along with the capacity, each edge will have a lower bound, which is 1.
Claim:
If every unit of flow created on the source reaches the sink maintaining the lower bound, then we can create a structure s such that G(s) = g.
Proof:
For each edge (u,v) where u is a vertex on the left and v is a vertex on the right, if the amount of flow gone through this edge is X then we can place X blocks of color u on top of X blocks of color v. The lower limit makes sure that there is at least one corresponding block pair for every edge of g.
The second subproblem is to calculate W(g): This is another easy exercise of dynamic programming using bitmask. (it is left as an easy exercise for the reader!)
A C++ implementation follows:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
int n, Min, Max;
vector < int > blockCnt;
int blockList[20][20], levelSize[10];
int cnt[777], dp[1 << 6], adjMask[10];
bool used[20], G[20][20];
const int INF = (1 << 29);
int GROUND, src, sink, cap[20][20];
// this method does what it says: "buildFlowNetwork()"
int buildFlowNetwork() {
GROUND = n + n;
src = GROUND + 1;
sink = src + 1;
int inDeg[10], outDeg[10];
memset(inDeg, 0, sizeof(inDeg));
memset(outDeg, 0, sizeof(outDeg));
memset(cap, 0, sizeof(cap));
int ret = 0;
for (int u = 0; u < n; ++u) {
for (int v = 0; v < n; ++v) {
if (G[u][v]) {
cap[u][v + n] = INF;
inDeg[v]++;
outDeg[u]++;
} else {
cap[u][v + n] = 0;
}
}
}
// src to node
for (int u = 0; u < n; ++u) {
cap[src][u] = blockCnt[u] - outDeg[u];
// to handle the lower limit we just subtract the amount of flow caused
// by the lower limit from the capacity
if (cap[src][u] < 0)
return -1;
ret += cap[src][u];
}
for (int i = 0; i < levelSize[0]; ++i) {
int x = blockList[0][i];
cap[x][GROUND] = INF;
}
cap[GROUND][sink] = INF;
// node to sink
for (int v = 0; v < n; ++v) {
cap[v + n][sink] = blockCnt[v] - inDeg[v]; // handling the lower limit
if (cap[v + n][sink] < 0)
return -1;
}
return ret;
}
int dfs(int u, int p[], int f) {
if (u == sink)
return f;
for (int v = 0; v <= sink; ++v) {
if (p[v] == -1 && cap[u][v] > 0) {
p[v] = u;
int btlnk = dfs(v, p, min(f, cap[u][v]));
if (btlnk > 0)
return btlnk;
}
}
return 0;
}
int flow() {
int ret = 0;
while (true) {
int p[20];
memset(p, -1, sizeof(p));
p[src] = src;
int f = dfs(src, p, INF);
if (f == 0)
break;
ret += f;
int v = sink;
while (v != src) {
int u = p[v];
cap[u][v] -= f;
cap[v][u] += f;
v = u;
}
}
return ret;
}
bool isValid() {
int required = buildFlowNetwork();
if (required < 0)
return false;
int f = flow();
return f >= required;
}
// this is the W(g) function that has been defined in the explanation section
// mask - represents the subset of vertices that has been picked up by Josh
int calcWays2(int mask) {
if (mask == ((1 << n) - 1)) {
return 1;
}
if (dp[mask] > -1) return dp[mask];
dp[mask] = 0;
for (int i = 0; i < n; ++i)
if (((mask >> i) & 1) == 0) {
if ((mask & adjMask[i]) == adjMask[i]) { // if all the vertices adjacent to i has been picked up
dp[mask] += calcWays2(mask | (1 << i)); // we can pick up i
}
}
return dp[mask];
}
int calcWays() {
memset(dp, -1, sizeof(dp));
return calcWays2(0);
}
// this method generates all possible graphs
// level - represents the level where we are placing blocks currently
// k - number of type of blocks that has been placed
// prev - the last block that was placed on the current level,
// this is used to make sure that for the current level, blocks are
// placed in increasing order of their id
void gen(int level, int k, int prev) {
if (level > 0 && levelSize[level - 1] == 0)
return;
if (k == n) {
if (levelSize[level] == 0)
return;
if (isValid()) {
int w = calcWays();
if (Min <= w && w <= Max) {
cnt[w]++;
}
}
return;
}
for (int i = prev + 1; i < n; ++i)
if (!used[i]) {
blockList[level][levelSize[level]++] = i;
// blockList[level] is a list of blocks placed on Level 'level'
used[i] = true;
if (level > 0) {
int m = levelSize[level - 1];
// here we take all possible subset of the blocks of the previous
// set and add edge from i to those in the subset
for (int j = 0; j < (1 << m); ++j) {
for (int a = 0; a < m; ++a)
if ((j >> a) & 1) {
int x = blockList[level - 1][a];
adjMask[i] |= (1 << x);
G[i][x] = 1;
}
gen(level, k + 1, i); // stay at the same level
gen(level + 1, k + 1, -1); // move up to a new level
// this loop undo the recent action
for (int a = 0; a < m; ++a)
if ((j >> a) & 1) {
int x = blockList[level - 1][a];
adjMask[i] ^= (1 << x);
G[i][x] = 0;
}
}
} else {
gen(level, k + 1, i); // stay at the same level
gen(level + 1, k + 1, -1); // move up to a new level
}
used[i] = false;
levelSize[level]--;
}
}
class CosmicBlocks {
public: int getNumOrders(vector < int > blockTypes, int minWays, int maxWays) {
blockCnt = blockTypes;
Min = minWays;
Max = maxWays;
n = blockTypes.size();
memset(cnt, 0, sizeof(cnt));
memset(used, 0, sizeof(used));
gen(0, 0, -1); // here we go!
int ret = 0;
for (int i = minWays; i <= maxWays; ++i) {
ret += cnt[i];
// cnt[i] is the number of fundamentally different structures s having W(s) = i
}
return ret;
}
};