June 25, 2012
SRM 547

DURATION
25 mincategories
Tags
share
Match Summary
Round Overview
Discuss this match
SRM 547 was a quite hard problem set compared to recent matches. But in every problem, except for Div1-Hard, solutions could be coded quite quickly once you figured out the correct approach. As a result of the match in Div1 Blue.Mary got his first win with quite fast solutions for Easy and Medium and 4 successful challenges, second place goes to SierraQuebecand the third one is tourist. In Div2 first place goes to ilya_malinovsky. He got amazingly fast submissions for all three problems and 7 successful challenges. New comer fenyan21 got the second place, and Neroysqis the third one.
MinimalTriangle
Problem Details
Used as: Division Two - Level One:
| Value | 250 |
| Submission Rate | 521 / 649 (80.28%) |
| Success Rate | 480 / 521 (92.13%) |
| High Score | iamtechaddict0 for 249.99 points (0 mins 10 secs) |
| Average Score | 184.98 (for 480 correct submissions) |
Let’s assume that we have regular hexagon ABCDEF (see the picture). After trying to look over all possible ways to divide hexagon with 3 diagonals we can see that the smallest area always equals to the area of triangle ABC.
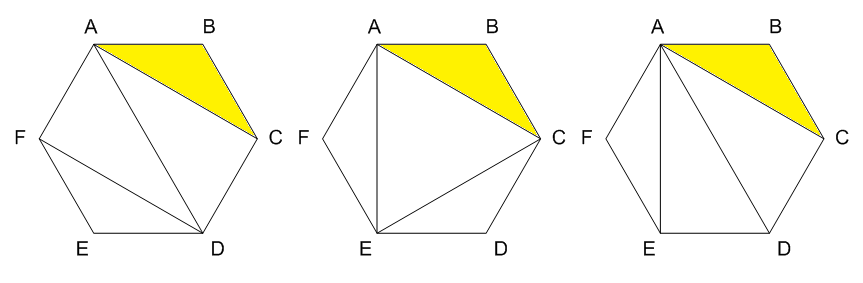
Than we just need to calculate this area. There are a lot of ways to do that, for example, area(ABC)=0.5ABBCsin(ABC), from the statement we can easily obtain that AB=BC=length, and angle ABC equals to 120 degrees and sin(120)=0.5sqrt(3). So the answer to this problem is 0.52*sqrt(3)*length2.
Also we can easily solve that problem if we know that the area of trianlge is “quadratic” function of its sides. So, from sample we obtain that the answer for length=5 is 10.825317547305485 hence for arbitrary length answer is 10.825317547305485/52 * length2.
Used as: Division Two - Level Two:
| Value | 500 |
| Submission Rate | 327 / 649 (50.39%) |
| Success Rate | 124 / 327 (37.92%) |
| High Score | vkot for 463.13 points (8 mins 8 secs) |
| Average Score | 316.36 (for 124 correct submissions) |
To solve this problem we can use following DP. Let dp[i][j] be the longest possible length to join ends of the first i pillars, where j is the height of the pillar i. Then,
1 2 3 4dp[0][j] = 0.0, for every j = 1..height[0] for i = 0..(N - 2), j = 1..height[i + 1] dp[i + 1][j] = max(dp[i][k] + length[j][k]), k = 1..height[i]
where length[j][k] is the length between two consequitive pillars with heights j and k, with simple geometry we obtain length[j][k]=sqrt(w2+(k-j)2) And the final answer is max(dp[N-1][j]), j=1…height[N-1].
Note: There is a O(N) solution.
Hint: Try to prove that in optimal solution the height of the pillar i equals 1 or height[i] for every i=0…N-1.
RelativelyPrimeSubset
Problem Details
Used as: Division Two - Level Three:
| Value | 1000 |
| Submission Rate | 133 / 649 (20.49%) |
| Success Rate | 16 / 133 (12.03%) |
| High Score | fenyan21 for 868.99 points (11 mins 23 secs) |
| Average Score | 553.22 (for 16 correct submissions) |
First let’s factor every number from the set. Than if number is divisible by prime number p>=50 than we can definetily include this number to our set T (obviously this number equals to p, and because all numbers are different than p is relatively prime with every other number from the set).
So we’ll include all prime numbers >=50 from S to our set T. Then every other number contains prime divisors <50. The crucial observation at this point is that there are just 15 prime number less than 50.
Then we will calculate dp[i][mask], which means maximal number of the first i elements from S which are pairwise relatively prime and contain prime divisors from mask.
Let divisors[i] be the bitmask of 15 elements which shows the prime divisors of S[i].
Then if mask contains divisors[i+1] we have
dp[i+1][mask]=max(dp[i][mask], dp[i][mask^divisors[i+1]]+1),
in other case
dp[i+1][mask]=dp[i][mask].
And the final answer is:
max(dp[N-1][mask]), mask=0…(2^15-1),
where N is the number of elements in S.
Used as: Division One - Level One:
| Value | 250 |
| Submission Rate | 446 / 478 (93.31%) |
| Success Rate | 291 / 446 (65.25%) |
| High Score | xiaodao for 249.29 points (1 mins 31 secs) |
| Average Score | 179.12 (for 291 correct submissions) |
After reading the problem statement one can easily code O(x*y) solution. Just go over all possibilities, add the results and after that divide by (x*y). Obviously this solution wouldn’t pass system tests. So we need to come up with something else.
Let’s have a look at the sum of all possible lengthes. Let d(i, j) be the length between two pillars with heights i and j. Then we have the following sum:
S=d(1,1)+d(1,2)+…+d(1,y)+d(2,1)+d(2,2)+…+d(2,y)+…+d(x,1)+…+d(x,y).
Obviuosly d(i,j)=d(j,i) and d(i-1,j-1)=d(i,j). We can assume that x<=y and then:
S=d(1,1)+d(1,2)+…+d(1,y)+d(1,2)+d(1,1)+d(1,2)+…+d(1,y-1)+…+d(1,x)+d(1,x-1)+…+d(1,y-x+1).
Let f(n) be the sum d(1,2)+…+d(1,n). Then
S=f(y)+f(1)+d(2,2)+f(y-1)+f(2)+d(3,3)+f(y-2)+…+f(x-1)+d(x,x)+f(y-x+1).
But this sum consists of only O(max(x,y)) numbers! So we can easily calculate the values of f(i) first and then calculate our sum. And in total it will be O(max(x,y)) which easily passes the system tests.
Used as: Division One - Level Two:
| Value | 500 |
| Submission Rate | 152 / 478 (31.80%) |
| Success Rate | 53 / 152 (34.87%) |
| High Score | WJMZBMR for 448.06 points (9 mins 54 secs) |
| Average Score | 256.58 (for 53 correct submissions) |
Let’s suppose that we have a subrectangular with sides p and q and the sum S of the elements. Then we can see that p<=height and q<=width, so p,q<=10^6.
Let a be the top-left element of the subrectangular, then after doing some maths we can obtain that
2*S=2*a*p*q+p*(p-1)*q*width+p*q*(q-1),
so 2*S is divisible by (p*q). In particular p, q are divisors of 2*S. So we can just go over all divisors of 2*S, which are less than or equal to 10^6 and check all of them. This solution nearly passes the system tests, because the number of divisors of 2*S is quite small, in worst case there are about 5000 divisors. One additional observation is that if p*(p-1)*q*width+p*q*(q-1)>S that we don’t need to check values greater than q. After this obvious observation we obtain a solution which passes all system tests.
MaximalTriangle
Problem Details
Used as: Division One - Level Three:
| Value | 1000 |
| Submission Rate | 3 / 478 (0.63%) |
| Success Rate | 0 / 3 (0.00%) |
| High Score | null for null points (NONE) |
| Average Score | No correct submissions |
This is quite hard optimizational problem. Only 3 contestans managed to submit something during the coding phase, but no one succeed after the challenge phase. Only ACRush was really very close to the right solution, but he didn’t consider test cases where z=1, he just forgot to return answer modulo 1. In all other cases his solution works pretty good.
Let’s consider the O(n^4) solution first. The idea is following:
Fix side lengthes of the triangle with maximal area.
Then we have 3 parts of our regular polygon and for each part we can calculate dp[i] - how many ways to divide part with i sides into triangles which has areas less than maximal (which is already fixed)
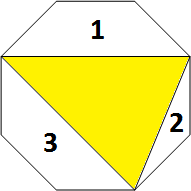
To calculate dp[i] we need to fix the triangle with the longest side and after that we’ll obtain two smaller parts. So, if A_1, A_2, …, A_i are the vertices of our polygon, then
dp[i]=sum(dp[j]*dp[i-j]) where area(A_1,A_j,A_i) is less than maximal_area
Now we have O(n^4) solution, because we have O(n^2) different triangles and we need O(n^2) to calculate the dp for each case.
This solution wouldn’t pass system tests, so we need to make some additional observations. Here they are:
If side lengthes are a, b, c, then we need calculate dp[i] for all i<=max (a,b,c).
If i is small, and every triangle in this “sub-polygon” has area less them maximal_area, then dp[i]=c[i-1], where c[i] - is i-th Catalan’s number. The triangle with maximal area is (A_1,A_(i/2),A_i). (It can be seen from the fact that area of trianlge equals to 0.5*height*side_length).
Calculation of dp[i] is symmetric if i is fixed (if we have dp[j]*d[i-j] in the sum, then we have dp[i-j]*dp[j] as well). So we can reduce number of computations 2 times.
Signed 64-bit type can store number up to 8*10^18, so when calculating dp[i] we can make additions with out “mod” operation, and make “mod” operation after our result is greater than 8*10^18. It will reduce running time at least 8 times.
It’s hard to estimate the complexity of this solution, but the maximal case is obvious, and with all this optimizations solution works in 1 sec. To better understanding see the writer’s solution in the practice room.