February 18, 2012
SRM 533

DURATION
30 mincategories
Tags
share
Match Summary
Round Overview
Discuss this match
Hello, I’m the writer of SRM533, cgy4ever, and this is my 3rd time to write a SRM (as well as the editorial).
The problem set
In DIV-I, contestants faced 2 algorithmic and tricky problems: 250p and 500p. The last one, 1000p, has the difficulty in both algorithmic and implementation. And the challenge phase is so active, due to the trick in 500p and some unexpected reason in 250p.
In DIV-II, the first 2 problem are a bit easier than normal, while the 1000p really need a lot of work in implementation, and have many details to handle. And the challenge phase is also active, with the same reason to 500p(which is the easier version of DIV-I 250p).
The story
1. Thanks to Google (This round is sponsored by google), there are 2150 contestants registered, which hits the maximum number. (This kind of thing happend rarely, the most recent round before that with this fact is SRM500.).
2. Before this round, many employees from google, include our famous players, Petr, chated with us in the Google Chat Lobby.
3. In DIV-I, the 1000p is really tough, even out of our expect. 5 minute before the end of contest, no one submitt this problem. So we worry about that maybe no one will accept, and this problem will be the second problem that I writed and no one solved.
4. Then suddenly we received one solution, it’s from bmerry, and he get passed (admins can see the result very soon)! But unfortunately, his 500p has a bug, so we afraid that no one can solve all 3 problems.
5. In the last 1 minute (56 seconds to the end), Petr submited his 1000p, accept! We were going to celebrate his win -- but, it’s too early to say who is the winner.
6. It’s just 5 seconds to the end, bmerry resubmitted his 500p to fix his bug. Then he become the second one to solve all 3 problems! So the challenge phase is so important, who will be the winner? Petr or bmerry-- oh, it’s also too early to say that the winner will be one of them.
7. The challenge phase begins! We left one trick in the 500p to be an opportunity to challenge, otherwise the challenge phase will be quite and boring -- that’s what we decided before the contest, since the examples for other 2 problems are very strong.
But the fact break our imagination: so many 250ps get challenged, even in the first minute. The reason is: many people sumbit a greedy solution, which can pass all the examples. We don’t consider this algorithm, so we didn’t create examples to beat this greedy.
8. In the first minute, tourist get 4 successful challenges! So maybe he can beat Petr.
9. So the challenge phase in DIV-I becomes extremely busy! And the result is: we received 502 challenge requests in total. And this round becomes one has most changes in DIV-Iall over the history of regular SRMs!
10. In the end, the only 2 contestants who solved 3 all problems, Petr and bmerry, none of them becomes the winner. One reason is: they all resubmit their 500ps caused by the tricky.
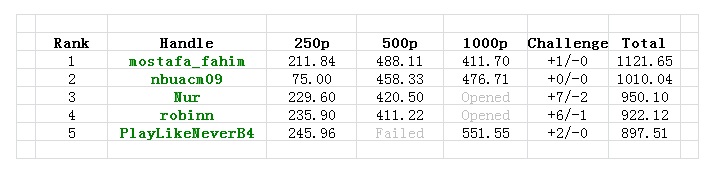
11. Our winner is tomek, due to his excellent performance in the challenge phase, congratulations again!
12. We may heard some remarkable storys between our long-historical Top-Coders: bmerry, tomek and Petr. But now, in 2012, this legendary still continues!
The winners
DIV-I
Used as: Division Two - Level One:
| Value | 250 |
| Submission Rate | 1316 / 1412 (93.20%) |
| Success Rate | 909 / 1316 (69.07%) |
| High Score | wilsonqoo for 249.96 points (0 mins 22 secs) |
| Average Score | 207.36 (for 909 correct submissions) |
Problem description
In this problem, we define the language Pikachu = {S[0]S[1]…S[k] | k>=0 , S[i] = “pi” or “ka” or “chu”} over the alphabet ‘a’ to ‘z’. For any input string S with the length no longer than 50, you are asked for determine whether S in Pikachu.
Solution 1
Let’s start with an example (The example case 5):
S = “chupikachupipichu”
We have the following reasoning:
Since the first letter of S is ‘c’, if S is in Pikachu, then S[0] must be “chu”, since “pi” and “ka” are not starting with the letter ‘c’.
So we could obtain: If S start with “chu”, then S in Pikachu if and only if the left part(we delete the prefix “chu” of S) is in Pikachu, otherwise, S can’t in Pikachu.
In this example, we have S = “chu” + “pikachupipichu”, so we reduce this problem into:
S = “pikachupipichu”
This time, S start with ‘p’, so we only need to consider “pi”. Luckly, S is starting with “pi”, so it can be reduced to:
S = “kachupipichu”
We repeat this procedure. Once S becomes an empty string, we could conclude: S is in Pikachu.
What about the case that S start with a letter different from ‘p’, ‘k’ and ‘chu’? In that case, S must not in Pikachu.
We can conclude above reasoning into the following code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public class PikachuEasy {
public String check(String word) {
int len = word.length();
word = word + "XX"; // (*) We append some letters that doesn't in 'a' to 'z' for convenience.
for (int i = 0; i < len; i++) {
if (word.charAt(i) == 'p') // First, we try "pi".
{
if (word.charAt(i + 1) != 'i') // The line (*) ensure that word has the index i+1.
return "NO";
i++;
} else if (word.charAt(i) == 'k') // And then we try "ka"
{
if (word.charAt(i + 1) != 'a')
return "NO";
i++;
} else if (word.charAt(i) == 'c') // We try "chu".
{
if (word.charAt(i + 1) != 'h')
return "NO";
if (word.charAt(i + 2) != 'u')
return "NO";
i += 2; // Since "chu" has the length 3, we should move i by 2 here.
} else
return "NO"; // If S doesn't start with 'p', 'k' or 'chu', then we halt and reject.
}
return "YES"; // If we parsed the whole string, then we accept.
}
}
The key of this argument based on this fact: “pi”, “ka” and “chu” start with different letter. If we change this strings to some others, then this problem will become more complicated.
Solution 2
If you have the knowledge in formal languages, then you would found:
The language Pikachu is a regular language.
So we can use regular expression to determine whether S is in Pikachu.
The following solution is provided by our admin ivan_metelsky.
1 2 3 4 5public class PikachuEasy { public String check(String word) { return word.matches("((pi)|(ka)|(chu))*") ? "YES" : "NO"; } }
Incorrect solution
Some players come up with the following solution very fast:
We clear all “pi” in S, then clear all “ka” in S, and clear all ‘chu’ in S. Then return “YES” if and only if S becomes empty.
How to challenge this? Oh, it’s something like “pkai”, I even think this solution is so clever and correct when I see this solution.
CasketOfStarEasy
Problem Details
Used as: Division Two - Level Two:
| Value | 500 |
| Submission Rate | 956 / 1412 (67.71%) |
| Success Rate | 585 / 956 (61.19%) |
| High Score | SEP1024 for 491.17 points (3 mins 49 secs) |
| Average Score | 324.98 (for 585 correct submissions) |
Problem description
Given an array A of positive integers: A[0] to A[n-1], you can do the following operations to get scores:
choose an index i: 0 < i < n-1, delete A[i], get the score A[i-1]*A[i+1], and relabel this array.
Your task is to return the maximal sum of scores.
Solution 1
Since we have |A| <= 10, an exponential algorithm could work.
Let’s analyze the total choice we have:
At the beginning, we have to choose one index out of n-2. When we have deleted one integer, next we have n-3 choice, etc.
Totally, there are no more than (n-2)! possible choice. And we have: (10-2)! = 40320, so we can simulate this procedure and try all possible choice.
This simulation can be done by using DFS (Depth-first_search).
We could define a function f(A) equals to: the maximal sum of scores when we start with the array A.
And we try all possible index i, record the maximum over all these |A-2| choice.
When we choose an index i, how can we calculate the maximum on this choice?
First, we know that the energy we obtained for this operation is A[i-1]*A[i+1]. Then the array becomes A[0], …, A[i-1], A[i+1], …, A[n-1], let’s denote it by A’.
So we can call f(A’), it will be the maximum of total energy we can obtain for the next operations.
Then we have: f(A) = max{A[i-1]*A[i+1] + f(A’)} for all valid i.
The following is an implementation of this idea, which is provided by our admin rng_58.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import java.math.*;
import java.util.*;
public class CasketOfStarEasy {
public int func(int[] a) { // Return the answer to the input a[].
int N = a.length, i, j, ans = 0;
for (i = 1; i < N - 1; i++) { // We try all possible i, from 1 to N-1, inclusive.
int b[] = new int[N - 1]; // if we discard the i-th element, this array will become b[].
for (j = 0; j < N - 1; j++) b[j] = a[j + ((j >= i) ? 1 : 0)]; // This is a tricky for calculating b[].
int tmp = func(b) + a[i - 1] * a[i + 1]; // a[i-1]*a[i+1] is for the current operation, and func(b) for the next operations.
ans = Math.max(ans, tmp);
}
return ans;
}
public int maxEnergy(int[] weight) {
return func(weight);
}
}
Note that this method uses some ideas of DP (Dynamic Programming). And we can use the memoization to obtain an O(2^n * n) solution.
Solution 2
This problem is also used as DIV1-Easy, but the constraint is different: |A| can be 50.
See the section of “CasketOfStar” of the analysis, which needs some insight views of this modul. And it’s an O(n^3) DP.
Incorrect solution
Please see the part “Incorrect solution” of DIV-I Easy: CasketOfStar.
Used as: Division Two - Level Three:
| Value | 1000 |
| Submission Rate | 39 / 1412 (2.76%) |
| Success Rate | 4 / 39 (10.26%) |
| High Score | PlayLikeNeverB4 for 551.55 points (31 mins 40 secs) |
| Average Score | 463.28 (for 4 correct submissions) |
Problem description
This problem introduced a model that much like a Role-playing game:
You start with M LP (Life Point), your LP automatically decreased by one for each day. The only way of gain LP is battle with witches.
For each witches, you can choose battle or not, and you know the possibility of win. In case of win, your LP increased by a given value, and if you lose, die immediately.
Your task is to find an optimal strategy that can maximize the index of days you die in the average.
Solution
Wow, this problem seems to be very complicated. Yes, that’s right. :)
But the algorithmic idea behind the solution is normal. Not too hard to see, it is DP (Dynamic Programming).
So let’s analysis this problem in a DP way.
In term of DP, you must have to design states, a state corresponding to a sub-problem.
And for this kind of game-like model, normally a state corresponding a profile that you have: the time in game, your property, the status of enemy, or something else.
In this problem, the time is “day” in game, and your property is LP. What about the status of enemy? It’s a little bit complex.
Note that: the status can’t be determined by “day”, since on one day, more than 1 witches may appear.
And you can’t use the 2-based mask to encode this information, since if all witches appear in one day, then the number of different masks will become 2^N , where N can be 50.
So we need to think about how to deal with the cases that lots of witches appear in one day.
Analysis of a single day
Suppose today is day i, and there are k witches that appears today: witch[0], witch[1], …, witch[k].
Now let’s think about this question: What is a strategy for today?
In the problem statement, we know that: “If multiple witches appear on the same day, you have to fight them one at a time”. So one of the possible strategy may looks like:
“I’ll fight witch[5] first. And there are 2 outcomes: win or lose. The action after that is related to this comeout.
In case of win, I’ll fight the next witch: witch[8], and there also have 2 outcomes, etc.”
It looks very complex: we have a strategy tree with at most k level, and there can be 2^k different outcomes.
Wait! What about the part “In case of lose”? Oh, It will looks like:
“If I lose, then I’ll die, and there will be nothing for me to think and determine.”
Yes, In case of lose, this strategy tree terminated and the game is over.
So the strategy can be always described with the following format:
Fight witch[a] first. If win, fight witch[b]. And if win again, fight with witch[c], etc.
We can denote (a, b, c, …) by S, which is an sub-set of {1,2,…,k}.
So every strategy corresponding to a list. Now let’s consider one the most important part in this problem:
Does the order of this list matters?
We can analysis this problem in the following way:
We asked ourselves: What’s the outcome could be of this whole day while we use a strategy S?
“Only two comeouts: survive or not.”
It’s because this fact: If I lose on any battle, the outcome is same: our living time is i.
Since the probability of survive and the gained LP for the whole day is not related the order. We could conclud:
The order doesn’t matter.
So we can sort the witches by "day"s, in case of a tie, sort it in arbitrary order. And we force our solution to obtain this order.
A DP method required an “order”, now we have. So Let’s consider the DP part.
Dynamic Programming
Let’s return to the part of design states, since the day is determined by the witch, we only need these information for a profile: (currentWitch, currentLifePoint).
We have: DP[currentWitch][currentLifePoint] = maximum of living-time in average, in case I’m just now after Witch[currentWitch] appears(If I fight with her, then it should be: after the fight), and the LP becomes currentLifePoint.
For the details, we need the start state, one way is to add one imaging Witch and set her appears at day-0, you can check it in the code.
Then let’s consider the most complicated part of this DP: the transition formula.
Normally, in this kind of game-like model, thinking of the transition is the same with thinking the choices you can play, and the outcome you could get.
Suppose we have after witch[currentWitch]'s appear, and the LP is currentLifePoint. Now what can we do?
If currentWitch is the last one, then we have no choice: wait the Life point goes to zero and die. So we have the following code:
If (currentWitch == N-1) return day[currentWitch] + currentLifePoint
Otherwise, we have determine whether battle with the (currentWitch+1)-th witch. Our DP value will be the larger one of these two cases.
And there is a detail: if currentLifePoint - (day[currentWitch+1] - day[currentWitch]) is less or equals to zero, then we can’t wait for the day her appear, we only can wait for die.
Case #1: Don’t fight.
So the only thing changes is: our Life Point decreased automatically, by the value of day[currentWitch+1] - day[currentWitch]. So we have:
outCome1 = dp(currentWitch + 1, currentLifePoint - (day[currentWitch+1] - day[currentWitch]))
Case #2: Fight with her.
In this case, we have two outcome: win or loss.
If we loss, the thing could be easy: we die at day[currentWitch+1], and we have:
outCome2Loss = day[currentWitch+1]
And in the case of a winning, our LifePoint can be calcuated by:
lifePointAfterBattle = min(M, currentLifePoint - (day[currentWitch+1] - day[currentWitch]) + gain[currentWitch+1])
And we have:
outCome2Win = dp(currentWitch + 1, lifePointAfterBattle)
Combine the above possible 2 outcomes, we obtain:
outCome2 = (win[currentWitch+1]/100.0) * outCome2Win + (1.0 - win[currentWitch+1]/100.0) * outCome2Loss
So if currentWitch is not N-1 and currentLifePoint - (day[currentWitch+1] - day[currentWitch]) is positive, we have:
dp(currentWitch, currentLifePoint) = max(outCome1, outCome2)
Afterall, we finished our DP solution, it can run in O(N*M), so it can pass the system test.
Check the details in the following code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
public class MagicalGirl {
public double maxExpectation(int M, int[] d, int[] w, int[] g) {
int N = d.length;
double dp[][] = new double[N + 1][M + 1];
int day[] = new int[N + 1];
double win[] = new double[N + 1];
int gain[] = new int[N + 1];
boolean alreadyAdd[] = new boolean[N];
day[0] = 0;
// The following code is for sort. It's a Selecting Sorting, which runs in O(N^2).
for (int i = 1; i <= N; i++) {
int earliest = 100000000, which = 0;
for (int j = 0; j < N; j++)
if (!alreadyAdd[j])
if (d[j] < earliest) {
earliest = d[j];
which = j;
}
alreadyAdd[which] = true;
day[i] = d[which];
win[i] = w[which] / 100.0;
gain[i] = g[which];
}
// The DP part starts.
for (int i = N; i >= 0; i--) // We must do DP in decreasing order of i, since DP[i][x] depends on DP[i+1][y].
for (int j = 1; j <= M; j++) // for j, you can do it for any order.
{
if (i == N || (j - (day[i + 1] - day[i]) <= 0)) // In case of: you only have the choice to waiting the death.
dp[i][j] = (day[i] + j) * 1.00;
else {
int LifePointAfterBattle = Math.min(M, j - (day[i + 1] - day[i]) + gain[i + 1]);
dp[i][j] = Math.max(dp[i + 1][j - (day[i + 1] - day[i])], // Case: Don't Battle.
(1.0 - win[i + 1]) * day[i + 1] + // Case: Battle but loss.
win[i + 1] * dp[i + 1][LifePointAfterBattle]); // Case: Battle and win.
}
}
return dp[0][M];
}
}
Used as: Division One - Level One:
| Value | 250 |
| Submission Rate | 741 / 849 (87.28%) |
| Success Rate | 424 / 741 (57.22%) |
| High Score | tourist for 248.22 points (2 mins 24 secs) |
| Average Score | 182.35 (for 424 correct submissions) |
Problem description
You are given an array W with size N. The only operation you could do is the following:
Select an element W[i], delete it and get the score: W[i-1] * W[i+1].
Your task is to calculate the maximum of sum of the score you could obtain by the above operation.
Solution
Since N can be 50, the bruteforce algorithm can’t work. So we need some insight view of this model.
Let’s start by an example: We have W = {A, B, C, D, E, F, G}, and we operate as following: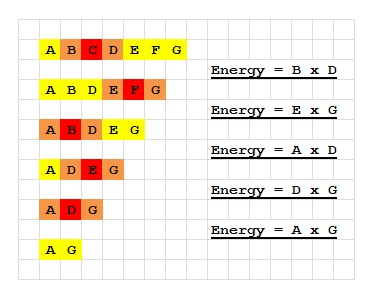
This means: we first select C, and delete it, obtain the energy B*D, and then select F, etc.
Usually this kind of problem have a DP solution, so let’s follow this idea first.
Hardness of normal DP
If we want to use some method like DP, or equally, search with memorization, we must estiblish a ‘state’.
Usually a state corresponding to a configuration of the board. Let’s try to encode the configuration:
One way of doing this is to use a binary integer: its i-th digit is 0 if and only if the i-th element in W was deleted.
But this method have a big problem: we have about 2^n different configuration, this solution must timed out.
Normally, when we find that, we could think: If all of this configuration may appear?
Hopelessly, indeed we have 2^(n-2) different configuration, since we can delete number at any position each time.
This fact based on the power of deleting, this operate can make this array to exponential number of outcome.
So, what about doing this reversely?
Do it reversely
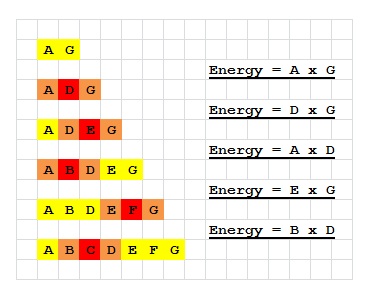
We make operations reversely:
The initial array is: {A, G}
First, we insert the element D, it looks like: {A, D, G}, we obtain energy: A x G.
Then we insert the element E, etc.
It’s easy to confirm: One possible operations in the original way corresponding to a way in this reversal version and they have the same total energy. (We only need to reverse the pictures as above).
So the deletions goes into insertions.
So what? How this changing makes it possibe to solve?
The thing we must care about is that the amout of energy we obtain when inserting element X.
It only depende on the current adjoining element. E.g. When we insert E in the above case, D and G is on the left and right to E, so the amount of energy is D*G.
Ok, now let’s analysis the function of insert an element, for example, the first one, the element D.
After this inserting, the array is separate into two part: {A, D} and {D, G}, what does it mean? If we insert element between A and D (i.e. B, C and D), it has the same effect when we deal with {A, B, C, D}, and the right part {D, G} is same.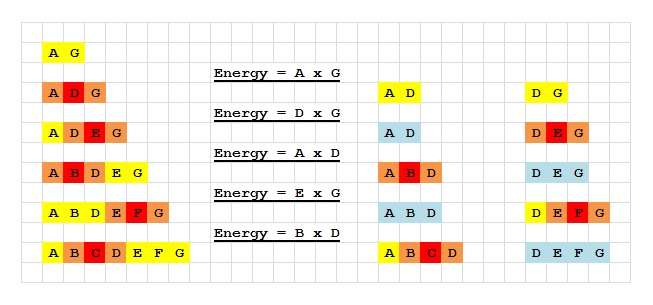
In the above figure, if we omit the blue background state, we could find, the energy we get from {A, D, G} to {A, B, C, D, E, F, G} is corresponding to the sum of energy we geted by make {A, D} to {A, B, C, D} and {D, G} to {D, E, F, G}.
The above idea is much like divide and conquer. Note that each sub-problem can be described by two parameters: L and R, where means we make {W[L], W[R]} to {W[L], W[L+1], …, W[R-1], W[R]}.
Then we come up a DP with O(N^2) state and O(N) transition. So the total complexity is O(N^3).
Please see the details in the following code.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18public class CasketOfStar { public int maxEnergy(int[] weight) { int n = weight.length; int dp[][] = new int[n][n]; // DP[i][j] is the answer to subsequence weight[i...j]. for (int d = 1; d < n; d++) // If DP[a][b] dependes on DP[c][d], we have: |c-d| < |a-b|, so we do DP in the order of (i-j). for (int i = 0; i + d < n; i++) { if (d == 1) dp[i][i + d] = 0; // {W[i], W[i+1]} => {W[i], W[i+1]} needs not any operation, so the answer is 0. else { dp[i][i + d] = 0; for (int j = i + 1; j < i + d; j++) if (dp[i][j] + dp[j][i + d] + weight[i] * weight[i + d] > dp[i][i + d]) dp[i][i + d] = dp[i][j] + dp[j][i + d] + weight[i] * weight[i + d]; // We try every element as the first one we insert. } } return dp[0][n - 1]; } }
What is the meaning in the normal sense?
Ok, this DP is not very normal. But what is the different?
Let’s describe above DP in the normal sense, not in case of reversal.
The state is normal. Let’s care about the transition.
What is the element that we enumerated? It’s the first one to insert in the reversal version. So it must be the last one to delete in the normal version.
So we also could obtain this DP if we can think about: “What is the one that be deleted in the last?”.
It’s hard, because that is not so easy to see, this element can separate this array into left part and right part.
Incorrect solution
So many players (both in DIV-I and DIV-II) come up the following unexpected greedy solution:
Each time we select the star such that we can get the max energy from this operation.
Why it is wrong? Oh, I even want to ask: why it is correct and why so many player come up with it, while all of 3 tests didn’t. :)
I don’t know some nice challenge cases for this algorithm yet, but some large random cases can be an option.
Ok, a nice challenge case: {1, 1, 1, 2, 3, 2, 1, 1, 1}
Used as: Division One - Level Two:
| Value | 500 |
| Submission Rate | 378 / 849 (44.52%) |
| Success Rate | 116 / 378 (30.69%) |
| High Score | meret for 469.79 points (7 mins 17 secs) |
| Average Score | 273.45 (for 116 correct submissions) |
Problem description
You are given a board, and some of the cells are marked.
Your task is to determine if there is way to visit all marked cell exactly once and satisfy the following condition: the first move is horizontal, the second is vertical, after which they alternate.
Solution
At first glance, the problem looks like a Hamiltonian Path, which is known as a NP-Complete.
However, we are given some additional conditions, so these conditions must be somehow special.
Before we go deeper into this problem, let’s start with an example:
This figure shows a way: A->B->C->D->E->F->G->H->I.
Some necessary conditions
Let’s analyse the conditions. Since rows and columns are symmetrical (more precisely, there is little difference between the two), let’s concentrate only on rows:
The problem statement says that A and B, C and D, E and F, etc. must in the same row.
After we pair them like that, we can make following observations:
1. If the total number of marked cells is even: all rows shall contain an even number of marked cells.
2. If the total number of marked cells is odd: all rows shall contain an even number of marked cells, except one, and it corresponds to the last visited cell.
In the figure above, there is an odd number of marked cells, so one of the marked cells in row 4 (I, in this case) will be the lasted visited cell.
Similarly, for columns, we have:
1. If the total number of marked cells is even: all columns shall contain an even number of marked cells, _except possibly for two columns, which will then correspond to the first and last cells._
2. If the total number of marked cells is odd: all columns shall contain an even number of marked cells, except one, which will correspond to the first visited cells.
The difference between rows and columns is that we can have two odd columns when there is an even number of marked cells.
So, we get some necessary conditions for rows and columns. If the board doesn’t satisfy these conditions, we simply return “NO”.
But are these conditions be sufficient?
No, and here is a counter-example.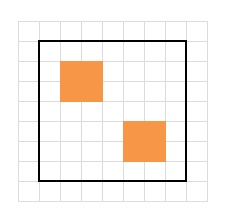
Each row/column has an even number of marked cells, but there is no solution.
Why? Because if we start in the upper-left region, we can’t reach the bottom-right region.
From that example, we can conclude that the marked cells should all be connected. We can describe this condition more formally as following:
We regard the marked cells as vertexes, and we link them with an undirected edge if two such cells are in the same row/column. The resulting graph should be connected.
We have these 3 conditions: rows, columns and connections. Are they sufficient?
The answer is yes, but it’s a bit hard to proove this directly, so we need to do some conversion.
The conditions on rows and columns are connected with odd and even numbers. What does that remind us of?
Eulerian Path
The necessary and sufficient conditions for an undirected graph to have an Eulerian path are similar to ours.
Let’s find the connection between them: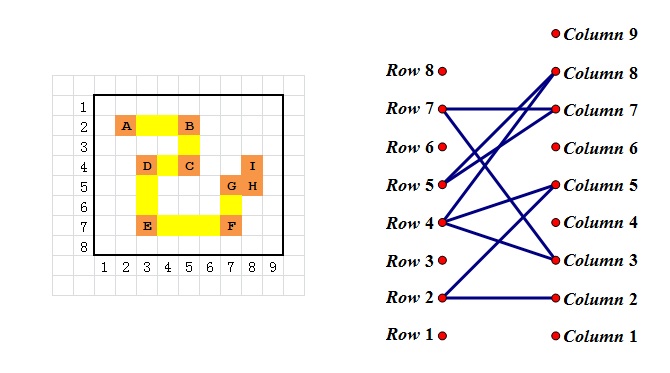
We establish a bipartite graph, the left part corresponds to rows, and the right part corresponds to columns.
For each marked cell (i, j), we add an edge to it connecting i-th row with j-th column.
From that, it’s easy to observe that the intend path corresponds to an Eulerian path in the corresponding graph.
Let’s see why: the conditions in problem statement become:
“S contains each cell with a Magic Diamond exactly once.” ==> “You must visited all edges.”
“For each even i, S[i] and S[i+1] are in the same row of board.” ==> “For each even i, the i-th edge and (i+1)-th edge must share the same vertexes in left part.”
“For each odd i, S[i] and S[i+1] are in the same column of board.” ==> “For each odd i, the i-th edge and (i+1)-th edge must share the same vertexes in right part.”
So we have successfully transformed our problem into an Eulerian path!
Now we only need to check if our conditions are sufficient.
The implementation is relatively easy, and is listed bellow.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
public class MagicBoard {
int n, m;
boolean haveAMark[][];
boolean visited[][];
int countDegreeForRow[];
int countDegreeForCol[];
void dfs(int x, int y) {
if (!haveAMark[x][y]) return;
if (visited[x][y]) return;
visited[x][y] = true;
for (int i = 0; i < n; i++)
dfs(i, y);
for (int i = 0; i < m; i++)
dfs(x, i);
}
public String ableToUnlock(String[] board) {
n = board.length;
m = board[0].length();
haveAMark = new boolean[n][m];
visited = new boolean[n][m];
countDegreeForRow = new int[n];
countDegreeForCol = new int[m];
int startX = 0, startY = 0;
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++) {
haveAMark[i][j] = (board[i].charAt(j) == '#');
if (haveAMark[i][j]) {
countDegreeForRow[i]++; // We count the degree of each vertexes in the corresponding graph.
countDegreeForCol[j]++;
startX = i;
startY = j;
}
}
int oddDegreeVertexes = 0; // We count the number of vertexes with an odd degree in the corresponding graph.
for (int i = 0; i < n; i++)
if (countDegreeForRow[i] % 2 == 1)
oddDegreeVertexes++;
for (int i = 0; i < m; i++)
if (countDegreeForCol[i] % 2 == 1)
oddDegreeVertexes++;
if (oddDegreeVertexes > 2) // The only case that this graph have an Eulerian path is: oddDegreeVertexes = 0 or 2.
return "NO";
if (oddDegreeVertexes == 2) // This part is really tricky. Note that: our path must start from right part.
{
boolean check = false;
for (int i = 0; i < m; i++)
if (countDegreeForCol[i] % 2 == 1)
check = true;
if (!check)
return "NO";
}
dfs(startX, startY); // Checking the connections.
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
if (haveAMark[i][j] && !visited[i][j])
return "NO";
return "YES";
}
}
Incorrect solution
Lots of contestants omitted this condition: the first move must be horizontal, and not vertical.
The easiest challenge case is {"#","#"}. My first reference solution to this problem also missed this, and got challenged by rng_58 with that case.
Used as: Division One - Level Three:
| Value | 1000 |
| Submission Rate | 4 / 849 (0.47%) |
| Success Rate | 2 / 4 (50.00%) |
| High Score | bmerry for 423.94 points (51 mins 8 secs) |
| Average Score | 418.20 (for 2 correct submissions) |
Problem description
Given N words with their frequency, your task is to encode them to strings that are the connection of “pi”, “ka”, “chu”.
These code must be prefix-free, and the goal is to minimize the average code length.
You are asked to answer both the total weighted code length and the number of ways to achieve this.
Solution
Let’s start by talking something a bit obvious.
First, there is no magic behand “Pikachu” ({“pi”, “ka”, “chu”}), the only thing matters is its length: {2, 2, 3}.
So if we change “Pikachu” into “Jirachi” ({“ji”, “ra”, “chi”}), the answer doesn’t change.
To see what does “prefix-free” means, let’s look at this prefix-free tree.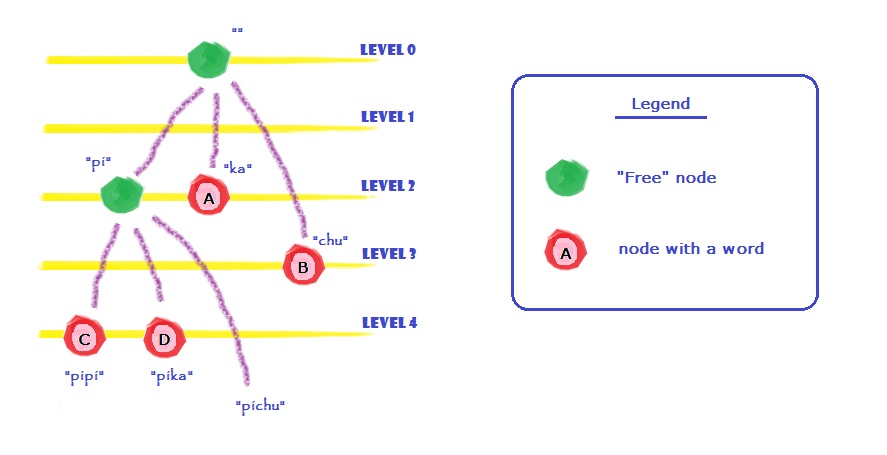
We have 4 words: A, B, C and D. And we encode them into “pipi”, “pika”, “ka” and “chu”.
This is an encoding problem, one related problem is Huffman code. And it’s 3-ary code, also, the costs are not unieque.
One easy observstion is (also used in the proof of Huffman’s algorithm):
If the above tree is optimal, then freq(A) >= freq(B) >= freq© , freq(D).
If not, then we can swap two of them, in order to obtain a more optimal solution, which is impossible.
Main idea
Unlike Huffman’s algorithm, we establish the tree from root to bottom.
We sort the frequency from larger to small. Then we can assign these words in this order.
Let’s see an example of a “state” when we do this:
Now we finished the level0 to level2, we assigend 1 word(of course one with the max frequency) already. And due to the previous operation, we have 1 free node in level3, 2 free nodes in level4 and 1 free node in level 5.
This is one “state” to obtain the tree in above figure. We have 5 parameters: last finished level: (l-1), number of assigned words, number of free nodes in level l+1, l+2 and l+3.
And what need we do in this level?
In level 2, we assign 1 word to one free node, and let another free node generate 3 branchs: two of them in level 4, and one in level5.
So in this level, we can assign some word to some free nodes, then other free nodes will each generate 3 new free nodes.
What about the total cost? Ok, we decompose this value for each node. Since we know what’s the current level, we can calculate the cost for this level: (number of words we assigned) * (current level).
This will lead one O(N^6) DP: O(N^5) states, and O(N) transition for solve the minimal total cost.
It’s enough for pass all the test for this problem, since N is only 30.
One optimization
And we can optimize this solution into O(N^4) states, by calculate the total cost in another way.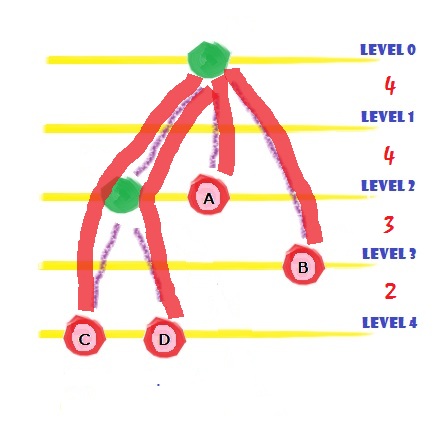
The total cost is total weighted length of these 4 red lines in above figure. We calculate them by sum them from each lines
But we can do this in another way: we consider the weighted length between each level: so we know:
Between level 0 and level 1, the total weighted length is: freq(A) + freq(B) + freq© + freq(D)
And since these words are in the order, if we know, we have 4 lines between this two level, we can get this value in O(1), if we prepare the prefix sum of freq[].
Look at the numer “4”, we already have this information in our DP: we know the number of assigned words, and N - (number of assigned words) = number of passed lines.
So we don’t need the information of which level we are stay.
And we get a DP that can run in O(N^5) for solving the minimal total cost.
Calculating the number of ways
One general method in calculating the ways in DP is like the following pseudo-code (Maybe it’s an valid code in Python)」コ
1 2 3 4 5 6 7 8 9 10ways(state): current_best = +INF current_ways = 0 for next_state in all_choices: if bestValue(next_state) < current_best: current_best = next_state current_ways = 0 if bestValue(next_state) == current_best: current_ways += ways(next_state) return current_ways
So the main idea is use this method, but there are still some details need us to consider.
For a certain level, it has F free nodes, and we want to assign A words to A of them. How many ways can we do this?
It is (C(F, A) * A!) ? Since we may choose A free nodes, and by the symmetry of the corresponding relationship between words and nodes, we have n! choice.
Yes, it’s almost correct, but miss one important cases! See the following example:
freq: [100 100 90] (90 80 80) 80 80 70 70
We already assigned 3 words(which its frequency in the “[]”), and now we want to assign 3 wordss in the current level.
By now we need choice 2 words with freq = 80 out of 4. So we have C(4, 2) choices.
For the general case, we need to consider the maximum of frequency that we need to assign in things level.(It is 80 in above example)
Then we count, how many words with this frequency have not been used (It is 4 in our case, let’s denote it by X), and how many words out of them that we want to assign. (2 in our case, let’s denote it by Y). Then we have C(X, Y) cases.
So we finish our calculating of ways. It’s a bit complicated.
Here is the reference program, you can check the details in it.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
import java.util.Arrays;
public class Pikachu {
int N, MOD;
int[] sigmaFreq;
int[] sameFreqFromL;
int[] sameFreqFromR;
int[][] C;
int[][][][] BEST;
int[][][][] WAYS;
long factorial[];
boolean[][][][] done;
int choice(int L, int R) // The number of ways that choose some words with frequency freq[L...R], inclusive.
{
L = Math.max(L, sameFreqFromL[R]);
if (L > R) return 1;
int R2 = sameFreqFromR[L];
return C[R2 - L + 1][R - L + 1];
}
void calc(int first, int nLevel0, int nLevel1, int nLevel2) // calc BEST and WAYS for the given parameters.
{
done[first][nLevel0][nLevel1][nLevel2] = true;
int theBest = 100000000;
long theWays = 0;
for (int useThisLevel = 0; useThisLevel <= nLevel0; useThisLevel++) {
int fSum = sigmaFreq[N] - sigmaFreq[first + useThisLevel - 1];
int freeNode = nLevel0 - useThisLevel;
int curCost = fSum + best(first + useThisLevel, nLevel1, nLevel2 + 2 * freeNode, freeNode);
if (curCost < theBest) {
theBest = curCost;
theWays = 0;
}
if (curCost == theBest) {
long curWays = 1;
curWays *= (long)(choice(first, first + useThisLevel - 1)) * factorial[useThisLevel];
curWays %= MOD;
curWays *= ways(first + useThisLevel, nLevel1, nLevel2 + 2 * freeNode, freeNode);
curWays %= MOD;
curWays *= C[nLevel0][useThisLevel];
theWays += curWays;
theWays %= MOD;
}
}
BEST[first][nLevel0][nLevel1][nLevel2] = theBest;
WAYS[first][nLevel0][nLevel1][nLevel2] = (int) theWays;
}
int calcBest(int first, int nLevel0, int nLevel1, int nLevel2) // The border case: nLevel0 + nLevel1 + nLevel2 >= number of left words.
{
int useLevel0 = Math.min(N - first + 1, nLevel0);
int useLevel1 = Math.min(N - first + 1 - useLevel0, nLevel1);
int useLevel2 = Math.min(N - first + 1 - useLevel0 - useLevel1, nLevel2);
int level0Lef = first, level0Rig = level0Lef + useLevel0 - 1;
int level1Lef = level0Rig + 1, level1Rig = level1Lef + useLevel1 - 1;
int level2Lef = level1Rig + 1, level2Rig = level2Lef + useLevel2 - 1;
return 2 * (sigmaFreq[level2Rig] - sigmaFreq[level2Lef - 1]) +
(sigmaFreq[level1Rig] - sigmaFreq[level1Lef - 1]);
}
int calcWays(int first, int nLevel0, int nLevel1, int nLevel2) // The border case: nLevel0 + nLevel1 + nLevel2 >= number of left words.
{
int useLevel0 = Math.min(N - first + 1, nLevel0);
int useLevel1 = Math.min(N - first + 1 - useLevel0, nLevel1);
int useLevel2 = Math.min(N - first + 1 - useLevel0 - useLevel1, nLevel2);
int level0Lef = first, level0Rig = level0Lef + useLevel0 - 1;
int level1Lef = level0Rig + 1, level1Rig = level1Lef + useLevel1 - 1;
int level2Lef = level1Rig + 1, level2Rig = level2Lef + useLevel2 - 1;
long ret = 1;
if (useLevel0 > 0) {
ret = (ret * choice(level0Lef, level0Rig)) % MOD;
ret = (ret * factorial[useLevel0]) % MOD;
ret = (ret * C[nLevel0][useLevel0]) % MOD;
}
if (useLevel1 > 0) {
ret = (ret * choice(level1Lef, level1Rig)) % MOD;
ret = (ret * factorial[useLevel1]) % MOD;
ret = (ret * C[nLevel1][useLevel1]) % MOD;
}
if (useLevel2 > 0) {
ret = (ret * choice(level2Lef, level2Rig)) % MOD;
ret = (ret * factorial[useLevel2]) % MOD;
ret = (ret * C[nLevel2][useLevel2]) % MOD;
}
return (int) ret;
}
int best(int first, int nLevel0, int nLevel1, int nLevel2) {
if (first > N)
return 0;
if (nLevel0 + nLevel1 + nLevel2 == 0)
return 100000000;
if (nLevel0 + nLevel1 + nLevel2 >= N - first + 1)
return calcBest(first, nLevel0, nLevel1, nLevel2);
if (done[first][nLevel0][nLevel1][nLevel2])
return BEST[first][nLevel0][nLevel1][nLevel2];
calc(first, nLevel0, nLevel1, nLevel2);
return BEST[first][nLevel0][nLevel1][nLevel2];
}
int ways(int first, int nLevel0, int nLevel1, int nLevel2) {
if (first > N)
return 1;
if (nLevel0 + nLevel1 + nLevel2 == 0)
return 0;
if (nLevel0 + nLevel1 + nLevel2 >= N - first + 1)
return calcWays(first, nLevel0, nLevel1, nLevel2);
if (done[first][nLevel0][nLevel1][nLevel2])
return WAYS[first][nLevel0][nLevel1][nLevel2];
calc(first, nLevel0, nLevel1, nLevel2);
return WAYS[first][nLevel0][nLevel1][nLevel2];
}
public int[] bestEncoding(int[] freq) {
// First we sort freq from large to small.
for (int i = 0; i < freq.length; i++)
freq[i] = -freq[i];
Arrays.sort(freq);
for (int i = 0; i < freq.length; i++)
freq[i] = -freq[i];
N = freq.length;
MOD = 1000000009;
sigmaFreq = new int[N + 1];
sameFreqFromL = new int[N + 1];
sameFreqFromR = new int[N + 1];
BEST = new int[N + 1][N + 1][N + 1][N + 1];
WAYS = new int[N + 1][N + 1][N + 1][N + 1];
done = new boolean[N + 1][N + 1][N + 1][N + 1];
C = new int[10 * N + 1][10 * N + 1];
factorial = new long[N + 1];
// Prepare C(a,b) and n! to ensure we can use them in O(1).
for (int i = 0; i <= 10 * N; i++) {
C[i][0] = 1;
C[i][i] = 1;
for (int j = 1; j < i; j++)
C[i][j] = (C[i - 1][j - 1] + C[i - 1][j]) % MOD;
}
factorial[0] = 1;
for (int i = 1; i <= N; i++)
factorial[i] = (factorial[i - 1] * i) % MOD;
sigmaFreq[0] = 0;
// The following preparation can ensure our solution run in O(N^5).
for (int i = 1; i <= N; i++)
sigmaFreq[i] = sigmaFreq[i - 1] + freq[i - 1];
sameFreqFromL[1] = 1;
for (int i = 2; i <= N; i++) {
if (freq[i - 1] == freq[i - 2])
sameFreqFromL[i] = sameFreqFromL[i - 1];
else
sameFreqFromL[i] = i;
}
sameFreqFromR[N] = N;
for (int i = N - 1; i >= 1; i--) {
if (freq[i - 1] == freq[i])
sameFreqFromR[i] = sameFreqFromR[i + 1];
else
sameFreqFromR[i] = i;
}
// Call the functions and let it calculat the answer.
int ans[] = new int[2];
ans[0] = best(1, 1, 0, 0);
ans[1] = ways(1, 1, 0, 0);
return ans;
}
}
You can also see the solution of bmerry, and the solution of Petr.