July 26, 2011
SRM 513


DURATION
25 mincategories
Tags
share
Match Summary
Round Overview
Discuss this match
SRM 513 reunited hundreds of coders from all over the world to compete and improve their algorithm skills. The problem set was perhaps simpler than usual, but it is always a challenge to get the best positions and this was a chance for the top coders to also show their speed skills in combination with dominance over algorithmic topics. It it is also the last match before the TopCoder Open’s Round 5, in which the big semifinalists are decided, it is no surprise that we saw many of them ready to warm up for the big challenge that awaits them.
The fastest time on the division 1 hard combined with also impressive performance in the other problems and 50 points in challenges allowed Petr once again to earn the crown with an advantage of more than 100 points over rejudge. The rest of the top 5 includes Jedi_Knight, Waaagh2 and rng_58.
In division 2, there were over 30 coders with more than 1000 points. In order to win like fajrinazis you would need to be consistently fast in all three problems. Or you can do like jbctaka and use challenging skills to get very close to the first place. Roma1995, StreetWalker and not_ scored the third, fourth and fifth places, respectively.
Used as: Division Two - Level One:
| Value | 250 |
| Submission Rate | 1046 / 1319 (79.30%) |
| Success Rate | 981 / 1046 (93.79%) |
| High Score | ajeet2009057 for 249.93 points (0 mins 29 secs) |
| Average Score | 170.91 (for 981 correct submissions) |
This is one of those problems that really just need you to do exactly what the statement says. For each student and each problem, find if the student has attended the classes for all the required topics. The student has to attent to all the required classes for that problem, but does not have to attend other classes to be able to solve it. There is no further complication as it just requires an O(N*K*M) loop. Commented Java code follows.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public String[] determineSolvers(String[] attendance, String[] problemTopics) {
int N = attendance.length;
int M = attendance[0].length();
int K = problemTopics.length;
String[] canSolve = new String[N];
//For each pair (student, problem):
for (int i = 0; i < N; i++) {
canSolve[i] = "";
for (int j = 0; j < K; j++) {
boolean can = true;
// If the student went through all of the problem's requirement
for (int k = 0; k < M; k++) {
if (problemTopics[j].charAt(k) == 'X') { // If the topic is a requirement:
// Then the student must have attended it:
can = can && (attendance[i].charAt(k) == 'X');
}
}
// Then put an X in canSolve[i][j] :
canSolve[i] = canSolve[i] + (can ? 'X' : '-');
}
}
return canSolve;
}
YetAnotherIncredibleMachine
Problem Details
Used as: Division Two - Level Two:
| Value | 500 |
| Submission Rate | 398 / 1319 (30.17%) |
| Success Rate | 255 / 398 (64.07%) |
| High Score | sharp.crazy for 491.51 points (3 mins 44 secs) |
| Average Score | 281.02 (for 255 correct submissions) |
Used as: Division One - Level One:
| Value | 250 |
| Submission Rate | 671 / 707 (94.91%) |
| Success Rate | 587 / 671 (87.48%) |
| High Score | vlad89 for 244.61 points (4 mins 14 secs) |
| Average Score | 184.08 (for 587 correct submissions) |
Each platform is at a different height. We can only move the platforms horizontally. We want to avoid the balls, not catch them.
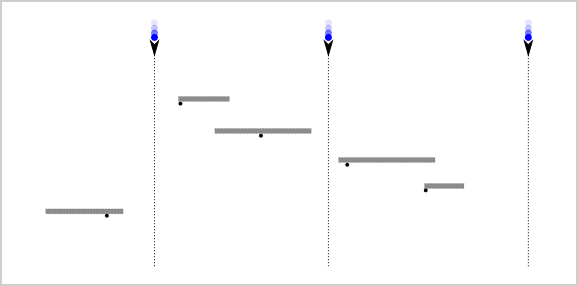
The positions we pick for a platform do not really affect the other platforms. They are independent of each other. Since they are independent, we can count the number of valid ways to place each individual platform and then multiply all the results together to find the final result.
We just need to count the number of ways to place a single platform. Let us begin with the rules about the mount point. “the leftmost possible position of the i-th platform is when its left end is at (platformMount[i] - platformLength[i], i + 1) and the rightmost position is when its right end is at (platformMount[i] + platformLength[i], i + 1)”. We do not need to worry about the vertical position, but let us call the current position of the platform the position in which its left end is located. Then the leftmost possible position is (mount - len) and the right most possible position is (mount), where mount and len are the platform’s mount point and length respectively. We will call those values the minimum and maximum values for the platform’s position - pmin and pmax.
However, those maximums and minimums are not yet the real maximum and minimum possible values for the position. The balls may also bound the platform’s locations.
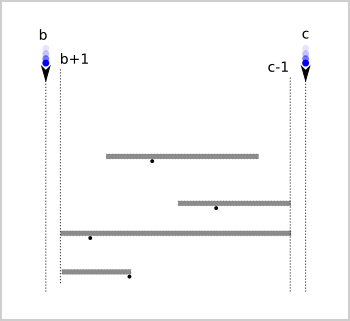
As the image shows, for every ball to the left of the platform, we need to make sure its leftmost end is strictly greater than the ball’s position (minimum platform position must be at least ball_position+1). For every ball to the right of the platform, the rightmost end must be strictly less than the ball’s position (maximum platform position must be at most ball_position-1-len). We can take each ball and update the platform’s maximum and minimum accordingly. At the end we will have two official values pmin and pmax.
It is possible that pmin ends up becoming larger than pmax. That happens when it is impossible to place the platform without getting hit by at least one ball. Then the range of allowed answers will be empty and there are 0 ways to place the platform. Otherwise, the number of ways to place the platform is simply the number of integers between pmax and pmin, inclusive: (pmax - pmin + 1).
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
public int countWays(int[] platformMount, int[] platformLength, int[] balls) {
final int MOD = 1000000009;
long res = 1;
int n = platformMount.length;
for (int i = 0; i < n; i++) {
int mount = platformMount[i];
int len = platformLength[i];
int pmax = mount;
int pmin = mount - len;
for (int ball: balls) {
// If the ball is to the left of the platform
if (mount >= ball) {
// Update minimum allowed value
pmin = Math.max(pmin, ball + 1);
}
// If the ball is to the right of the platform
if (mount <= ball) {
// Update maximum allowed value
pmax = Math.min(pmax, ball - 1 - len);
}
}
int ways;
if (pmax >= pmin) {
ways = (pmax - pmin + 1); //total number of ways
} else {
ways = 0; // Impossible to correctly place the platform
}
System.out.println(pmax + " ; " + pmin + " = " + i);
// multiply the results for each ball:
res = (res * ways) % MOD;
}
return (int)(res);
}
Excercise
Solve a different variation of this problem: find a way to locate all platforms so that the maximum amount of balls falls to the ground. You can first solve the task for the same constraints as in the original problem and then try to find as fast solution as possible.
The lengths of the platforms are actually not allowed to be larger than 10000. This means that there will be at most 10000 different positions to try for each for platform. A simple brute-force approach that tries every possible position and counts the ones that do not get hit by a falling ball is possible and will actually pass the time limit.
Used as: Division Two - Level Three:
| Value | 1000 |
| Submission Rate | 166 / 1319 (12.59%) |
| Success Rate | 44 / 166 (26.51%) |
| High Score | zgw4fun for 859.82 points (11 mins 52 secs) |
| Average Score | 596.74 (for 44 correct submissions) |
A common mistake was to believe that since in the examples the results are either to use only vertical blocks or only horizontal blocks, it would mean that this method would work for any input. The low constraints (at most 4x4) should be a sign that those behind the contest did not expect such a fast solution to be correct. In case the problem seems to be far easier than you would expect normally on that slot and the constraints seem also very small for the approach you are about to try, be skeptical and try to demonstrate your solution is correct or to find a counter example. In fact, test case #2 puts some emphasis on numbers with leading 0s. We can use it to build a counter example:
0005
0001
0001
5111
In this case, we need both a column and a row. Specifically, 5111 and 511. Going all rows or all columns will give only 5111+5+1+1.
How to correctly solve the problem then? As mentioned the constraints for this problem are very low (4 x 4) - brute force-based solutions are probably the intended ones in this problem. As you can see in the previous example, the issue is about possible intersections of columns and rows, and we need to distribute the cells correctly to columns and rows to maximize the solution.
If we first marked each cell as “horizontal-only” or “vertical-only”, then we would have a board like follows:
VVVH
VVVH
HHHH
VVHH
Given a marked board, the decision about using cells in vertical or horizontal blocks has already been made. So we no longer have to worry about how to assign the intersections. It should be simple to see that the solution for a given board marked like that is to make the largest possible vertical and horizontal blocks that can fit the rules of the marked board. It helps to interpret the marks of the board the following way:
_ _ _ _
|V|V|V|H|
|V|V|V|H|
|H H H H|
|V|V|H H|
To pick the largest blocks that fit those spaces reserved for vertical and horizontal blocks can be done with two O(N2 loops. We can see marking the board as picking a subset of the cells of the board and marking them as vertical while the complement is marked as horizontal. So, there are 2number of cells ways to mark the board. In a 4x4 board, there are 16 such cells. 216 is 65536. 6553644 is also a small number, so this approach will solve the problem.
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
public int maximumSum(String[] board) {
int w = board.length, h = board[0].length();
int t = w * h;
int res = 0;
// Use a bitmask to simulate finding all subsets of cells. Then use
// each subset to define which cell is marked as vertical or not.
for (int mask = 0; mask < (1 << t); mask++) {
int s = 0;
// For each column, find maximal vertical blocks:
for (int i = 0; i < w; i++) {
int x = 0;
for (int j = 0; j < h; j++) {
if ((mask & (1 << (i * h + j))) == 0) { //horizontal
s += x;
x = 0;
} else { // vertical
x = x * 10 + (int)(board[i].charAt(j) - '0');
}
}
s += x;
}
// For each row, find maximal horizontal blocks:
for (int j = 0; j < h; j++) {
int x = 0;
for (int i = 0; i < w; i++) {
if ((mask & (1 << (i * h + j))) != 0) { //vertical
s += x;
x = 0;
} else { // horzizontal
x = x * 10 + (int)(board[i].charAt(j) - '0');
}
}
s += x;
}
// Remember the best sum found so far:
res = Math.max(res, s);
}
return res;
}
Exercise
Solve the problem if the input boards can be as large as 6x6. Hintthe solution is still brute force, but it needs to be implemented carefully.
Used as: Division One - Level Two:
| Value | 500 |
| Submission Rate | 196 / 707 (27.72%) |
| Success Rate | 159 / 196 (81.12%) |
| High Score | Waaagh2 for 458.72 points (8 mins 40 secs) |
| Average Score | 262.09 (for 159 correct submissions) |
Note that the cards are revealed one by one. In every turn you can decide which second card to reveal based on what the first card is. Note also that the actual dimension do not really matter, only the total number of starting cards matters. Finally, given a number of cards W*H, there will be a number of pairs which you do not know where are located. We will call it unknown = W * H / 2.
The state of the game depends not only on the number of unknown pairs. That number determines the total number of pairs of which you have not found the position of any of its cards. There can also be some pairs for which you already know the position of exactly one of the cards, we will call the number of those pairs known1. If there were pairs of which you knew both positions, you could just pick them together in the next turn, so we do not need to consider those pairs when describing the state of the game. All unknown pairs are indistinguishible from each other. The same happens to the known1 pairs. Therefore we can describe the state of the game using just the pair (unknown, known1).
Let us pretend to play a turn. If we already know the contents of some cards, there is never a reason to reveal them as the first card in a turn (unless it is when we already found their pair). So we will reveal a card with unknown content. The total number of such cards is t = (2*unknown + known1). This is because there are (unknown + known1) total unmatched pairs and we already know the locations of one card per known1 pair.
There will be a probability that the first card we reveal contains a symbol that we have already seen before (one card out of the known1 pairs). In this case it only makes sense to reveal its pair as the second card of the turn (because we want to minimize the number of turns). This will make the pair revealed and matched and thus the state changes to (unknown, known1-1). Note that we used a turn to make this move. The probability is: p = known1 / t.
When the card is an unknown one (probability (1-p) or (2*unknown/t), we still need to pick a second card. If we picked a known1 card then we would not be making good use of the turn. It is better to pick another card of which we ignore the symbol. There is going to be a small probability to pick a pair of for the first card of the turn and at worst we will use the turn to find more information. Thus pick one of the cards with unknown symbols, there are three posibilities:
• The second card has the same symbol as the first one. Then we just decrease unknown by 1. The state becomes (unknown-1, known1). The total probability for this to happen is (1-p) * (1 / (t - 1) ). As there is only one card left among the unrevealed ones that has the same symbol as the first card and there are t-1 total unrevealed cards left. We used one turn.
• The second card is a different unknown card. We decrease unknown by 2 and increase known1 by 2. Because those two different unknown pairs became pairs with one known card. The new state is (unknown-2, known1+2). The probability for this to happen is: (1 - p)*(unknown*2 - 2)/(t-1). There will be t-1 cards left, of which we pick any of the two cards with the same symbol as the first card picked in the turn. We used one turn.
• The second card has the same symbol as one of the known1 cards: then we can match this card with its pair in the next turn, which means known1 is decreased. We also need to decrease the number of unknown pairs and increase known1 again (because when we revealed the first card, that pair of unknown cards become a pair of which you only need one card.) Note that we needed two turns in total, one to reveal the first two cards and another to match the second card we found with its already-known pair. The new game state is (unknown-1, known1). The probability for this to happen is (1 - p) * known1/(t-1).
This is enough to make a recurrence. For each case, we know the probability of that case and the number of turns it will take. The number of turns is based on a recursion. For example, in case we picked a known1 card, the game state becomes (unknown, known1-1) with a probability p. This can be translated to there being a probability equal to p that we will need 1+F(unknown, known1-1) moves. The sum of the products of each possible number of moves and its probability is the expected value.
Recurrences need base cases, in this case that happens when the total pairs left is 0. That means we matched all the possible cards and thus the result (the number of moves is 0). This recurrence is acyclic. The maximum number of pairs is 50*50/2 = 1250. We can use the recurrence and memoization as there will be at most 1250 x 1250 different game states / states for the recurrence.
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
import java.util.*;
public class PerfectMemory {
boolean[][] solved;
double[][] mem;
double rec(int unknown, int known1) {
// We use memoization to make sure each pair of arguments is evaluated
// at most once.
double res = mem[unknown][known1];
if (!solved[unknown][known1]) {
solved[unknown][known1] = true;
res = 1e100;
int t = unknown * 2 + known1;
if (t == 0) {
res = 0;
} else {
res = 1.0;
double p = (1.0 * known1) / t;
if (known1 > 0) {
// pick one of the known1 cards.
double p = (1.0 * known1) / t;
res += p * rec(unknown, known1 - 1);
}
if (unknown > 0) {
// pick one of the unknown cards:
// pick another random card
// by luck pick the pair of the previous card:
double q = 1 / (t - 1.0);
res += (1 - p) * q * rec(unknown - 1, known1);
// pick a different unknown card
if (unknown > 1) {
q = (unknown * 2 - 2) / (t - 1.0);
res += (1 - p) * q * rec(unknown - 2, known1 + 2);
}
// pick a card we found before.
if (known1 > 0) {
q = known1 / (t - 1.0);
res += (1 - p) * q * (1.0 + rec(unknown - 1, known1 + 1 - 1));
}
}
}
mem[unknown][known1] = res;
}
return res;
}
public double getExpectation(int N, int M) {
// set the number of card pairs.
int np = (N * M) / 2;
// prepare memoization arrays:
solved = new boolean[np + 1][np + 1];
mem = new double[np + 1][np + 1];
return rec(np, 0);
}
}
Used as: Division One - Level Three:
| Value | 1000 |
| Submission Rate | 48 / 707 (6.79%) |
| Success Rate | 13 / 48 (27.08%) |
| High Score | Petr for 686.27 points (21 mins 22 secs) |
| Average Score | 480.94 (for 13 correct submissions) |
Note that each mirror can only affect a single coordinate. And each of the normal moves can only increase or decrease one of the three coordinates. We can just treat each coordinate separately and then add the minimum distances for each coordinate together. More so, each of the coordinates has the same behavior. The problem can then be simplified to going from 0 to x possibly using a list of mirror positions of planes perpendicular to the x axis. We can just repeat the same approach for each of the axis.
After we have made that simplification, there are two more things to highlight. First, the maximum number of mirrors paralel to an axis is 20. Also importantly, you can use each of the mirrors at most once. These two constraints will be of use later.
The next thing is to notice how the mirrors actually work. Let us say a mirror is at position T and you are currently at position y. y may be either to the left or the right of the mirror, find y1, the coordinate after using the reflection.
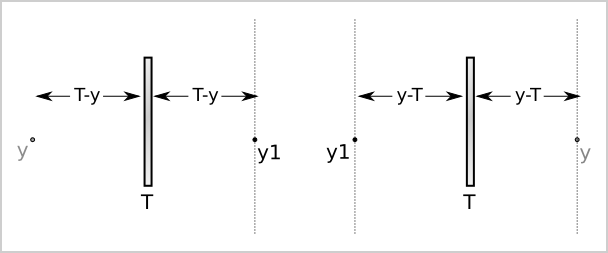
Let us calculate the value of y1 in both cases. In the first one, the result is: ( y1 = 2*T-y ), and in the other one the result is also ( y1 = 2*T-y ). This one is very useful. We do not have to worry about the relative position between the artifact and the mirror, using the reflection will always change the result from y to ( 2*T-y ).
From the previous observation, note that we can also verify that we can decide whether to use the mirror or not and use then before considering the normal moves that increase or decrease the coordinate, and it will not affect the final result. Let us try to verify it for only one mirror. If we wanted to move from a position current to the target x:
1. Assume that we have decided not to use the mirror. Then the result will be equal to abs( x - current).
2. If we decide to use the mirror, assume we use it before using the normal moves. Then the position becomes (2*T- current) and from then, the distance using only normal moves is: abs( x + current - 2*T). 3. If we decide to move before using the mirror, even by one step, and then we used the mirror, the final distance will be either: abs( x + current + 1 - 2*T) or abs( x + current - 1 - 2*T) depending on the direction we used. It can be shown that those values can not be smalelr than ( abs( x + current - 2*T)-1 ). If they were larger than that value, then approach #2 is better, if they were equal to that value, then the answer would be the same as if we used approach #2.
This can be generalized to any number of mirrors and any distance travelled before using the mirrors.
The problem has become to select a set of mirrors to use before using the normal moves and also to pick the order in which the mirrors are used. Note that the initial position is 0. Let us first focus on the order. Assume we will have decided to use two mirrors, one located at T and one at R. If we use T and then R the artifact location will first change to ( 2*T - 0 = 2*T) and then to (2*R - 2*T). If we use the other order, the position will change to (2*T - 2*R). In fact, after we picked the mirrors, the order does not matter as much as the parity of each mirrors (whether we use the mirror at an even or odd step number). The final position after using the selected mirrors will be of the form : 2*A - 2*B + 2*C - 2*D + 2*E + … Where A,B,C,D,E,… are the positions of the mirrors in some order. In other words, after selecting all the mirrors we would like to use, then for each mirror position T, we can decide whether to subtract 2*T or to add 2*T. Note however, that the number of subtractions and additions depend on each other. Only the following ways are valid:
2A
2A - 2B
2A - 2B + 2C
2A - 2B + 2C - 2D
etc.
In other words, the number of aditions and subtractions must be equal or the number of additions must be exactly one more than the number of subtractions. Let us call sign = (number of additions - number of subtractions). Then sign must be 0 or 1.
For each mirror, there are three choices: we can decide to not use the mirror, to use it in such a way that the final position will have a +2*mirror_position or to use it in such a way that the final sum will have a -2*mirror_position. And then we must verify that the numbers of positive and negative summands are valid. How about the following approach: try all possible combinations of options for each mirror (used, used positively, used negatively), then for each combination verify if it is valid. If it is valid, find the distance between the new position and x add the number of moves we used to use the mirrors. Minimize the total distance among all possible combinations.
That yields a O(3N * N) approach, where N is the number of mirrors. Although this is wrong, we will implement it anyway. There are many ways to iterate through all possible combinations. One is to use a recursive approach in a Backtracking way. Another way (that we will use) is just to try all natural numbers up to 3N. If we convert each of these numbers to base three, then we will have Ndigits that can be either 0, 1, or 2 (three choices) and we can use each number to represent a combination.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
//Single function that solves the case for a single coordinate and its list of mirrors.
long minMoves(int[] mirror, int x) {
int n = mirror.length;
// Prepare the powers of three, to decode the numbers.
int[] pow3 = new int[n + 1];
pow3[0] = 1;
for (int i = 1; i <= n; i++) {
pow3[i] = 3 * pow3[i - 1];
}
long res = Long.MAX_VALUE;
for (int mask = 0; mask < pow3[n]; mask++) {
int sign = 0;
long sum = 0;
int moves = 0;
for (int i = 0; i < n; i++) {
//Extract i-th digit
switch ((int)((mask / pow3[i]) % 3)) {
case 0: //Do not use the mirror
break;
case 1:
sum += 2 * mirror[i]; //use the mirror in a positive step
sign++;
moves++;
break;
case 2: //use the mirror in a negative step
sum -= 2 * mirror[i];
sign--;
moves++;
break;
}
}
// are the sign numbers valid?
if (sign != 0 && sign != 1) {
continue;
}
// The new position is then sum. We needed {moves} steps to use the mirrors.
res = Math.min(res, Math.abs(x - sum) + moves);
}
return res;
}
The approach is wrong simply because the 20 mirrors limit is too large for O(3N*N). 20 happens to be a number that is too large for such exponential approach. Yet it is still smaller than the more common constraint (50). If the constraint was lower, even just the half 10, then the problem would have been solved. In fact, there is a problem solving technique that is sometimes applicable when the constraint is too large for a basic exponential solution but half the size is actually a good condition. It is the meet-in-the-middle technique. You can find a very simple example for using that technique in the problem called KnapsackProblem. Basically, the meet-in-the-middle technique splits the sequence in two parts. So, instead of dealing with N mirrors we will deal with N/2 mirrors on each of the halves of the input (one half may have N/2+1 mirrors). As you can see, generating all combinations for each half (actually using the previous algorithm) will take at most 310*10 time. The trick in meet-in-the-middle approach is to find a way to combine the information from the two halves so that to find a solution for the larger problem.
Say we have split the input in two parts, A and B, and we have found all the possible combinations for each. Note that the condition regarding the number of positive and negative summands does not apply when getting the combinations for each half, but it will be important when merging the parts. So, there will be 2N/2 different combinations in each part. For each of those combinations, we know sign (subtraction between number of positive and negative steps), the total number of mirror moves it used num and the current sum of its values sum (equal to (2something - 2something_else + 2*…)). What we need is, given the data from one of the 2N/2 subjects from A, we need to find the most suitable item out of B. At the end, signA + signB must be 1 or 0. Something that we can do is to keep two tables A[], B[] such that A[t] will contain the data of all combinations with signA= t and a similar condition for B[]. Therefore, given a signA, we can iterate through the two valid values of signB: ( signA + signB = 0 ) and ( signA + signB = 1 ). And only consider the items that have those values.
Given sumA, numA and signA (the data about a certain combination of mirror moves from the A side) and a list of all the possible pairs (sumB, movesB) with the values from B that have a wanted signB value, we need to find the (sumB, movesB) that minimizes the total distance. Finding such pair is going to be difficult. So, how about changing the tables to have two dimensions? Then we have A[][] and B[][]. Table A[numA][signA] gives all the possible sums of numA elements from A such that the difference between positive and negative steps is signA. Then, for each sumA we will have to iterate for signB (two possible values) and also for numB. We will have a list B[numB][signB] of the possible sumB values given those circumstances. We need to find the best sumB such that:
abs( sumA + sumB - x ) is minimal.
That can be solved with some logic. The minimum value of abs(z) is either the positive value of z that is closest to 0 or minus the negative value of z that is closest to 0. So, we want the value of sumB such that:
minimum( sumA + sumB - x ) such that sumA + sumB - x >= 0.
maximum( sumA + sumB - x ) such that sumA + sumB - x <= 0.
max( sumB ) such that: (sumB <= x - sumA)
min( sumB ) such that: (sumB >= x - sumA)
In other words, we need to find the sumB that is as close as possible to (x - sumA). So we need to find the smallest element in a list that is > a value and also the largest element in a list that is < the same value. Assuming that the list is sorted, this is a common application of binary search.
A little analysis of complexity. We first need to pick all triples (sumA, numA, signA), with some analysis, you can see that there are at most 3N/2 of them. Then, we need to pick all values for signB, there are at most 2 valid ones for a given signA. Then we need all values for numB, this can be at most N/2. Finally, we need to do a binary search over all values of sumB that follow the condition. The maximum number of sumBvalues is 3N/2, the binary search is logarithmic and the logarithm of a power is equal to the exponent. In total, the complexity will be: O( 3N/2 * N * N ).
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
import java.util.*;
public class Reflections {
// For one of the halves of mirrors, finds all the possible 2*T - 2*R + 2*..
// The number of moves it takes to find that sum, and the subtraction (sign)
// of the odd and even moves. Then makes a table X[num][sign] that contains
// all the sums for the given num and sign.
//
long[][][] makeHalf(int[] from, int low, int right) {
int n = right - low;
int[] mirror = new int[n];
for (int i = 0; i < n; i++) {
mirror[i] = from[low + i];
}
int[] pow3 = new int[n + 1];
pow3[0] = 1;
for (int i = 1; i <= n; i++) {
pow3[i] = 3 * pow3[i - 1];
}
long[][][] ressum = new long[n + 1][2 * n + 1][];
// It is the same 3^N approach, we do two passes in order to first
// find the sizes of the list in each part of the table and then
// create those lists and add the elements.
for (int pass = 0; pass < 2; pass++) {
int[][] count = new int[n + 1][2 * n + 1];
// It uses base 3 numbers to generate the 3 possibilities
// for each mirror.
for (int mask = 0; mask < pow3[n]; mask++) {
int sign = 0;
long sum = 0;
int moves = 0;
for (int i = 0; i < n; i++) {
switch ((mask / pow3[i]) % 3) {
case 0:
break;
case 1:
// If we want the final sum to have a 2*mirror[i]
sum += 2 * mirror[i];
// Then we need:
sign++;
moves++;
break;
case 2:
// If we want the final sum to have a -2*mirror[i]
sum -= 2 * mirror[i];
// Then we need:
sign--;
moves++;
break;
}
}
if (pass == 1) {
ressum[moves][sign + n][count[moves][sign + n]] = sum;
}
count[moves][sign + n]++;
}
for (int i = 0; i <= n; i++) {
for (int s = -i; s <= i; s++) {
if (pass == 0) {
ressum[i][s + n] = new long[count[i][s + n]];
} else {
Arrays.sort(ressum[i][s + n], 0, count[i][s + n]);
}
}
}
}
return ressum;
}
long minMoves(int[] mirror, int x) {
int n = mirror.length;
int a = n / 2;
int b = n - n / 2;
long[][][] A = makeHalf(mirror, 0, n / 2);
long[][][] B = makeHalf(mirror, n / 2, n);
long res = Long.MAX_VALUE;
for (int numA = 0; numA <= a; numA++) {
for (int signA = -numA; signA <= numA; signA++) {
for (int signB = -signA; signB + signA <= 1; signB++) {
// ( signA+signB == 0 || signA + signB == 1)
// { -numB <= signB <= numB }
// numB >= -signB
// numB >= signB
for (int numB = Math.abs(signB); numB <= b; numB++) {
for (long sumA: A[numA][signA + a]) {
// find optimal sumB from B[numB][signB+b]
//minimize: ( abs(x - sumA - sumB) )
//minimize x - sumA - sumB >= 0
// max sumB such that:
// sumB <= x - sumA
//
//maximize x - sumA - sumB <= 0
// min sumB such that:
// sumB >= x - sumA
// Use a binary search, Java has it builtin in this case:
int p = Arrays.binarySearch(B[numB][signB + b], x - sumA);
if (p >= 0) { // sumA - x exists in the array
res = Math.min(res, numA + numB);
} else {
p = -p - 1;
// p is the first element greater than x - sumA
// the result could be at p, or p-1
if (p - 1 >= 0) {
long sumB = B[numB][signB + b][p - 1];
res = Math.min(res, Math.abs(x - sumA - sumB) + numA + numB);
}
if (p < B[numB][signB + b].length) {
long sumB = B[numB][signB + b][p];
res = Math.min(res, Math.abs(x - sumA - sumB) + numA + numB);
}
}
}
}
}
}
}
return res;
}
public long minimumMoves(int[] mirrorX, int[] mirrorY, int[] mirrorZ, int[] finalPosition) {
// The coordinates are independent, treat them separately
long res = 0;
res += minMoves(mirrorX, finalPosition[0]);
res += minMoves(mirrorY, finalPosition[1]);
res += minMoves(mirrorZ, finalPosition[2]);
return res;
}
}
As an alternate solution recall that our solution has the form 2 * (X1 + X2 + … + XN) - (Y1 + Y2 + … + YN/YN-1) . So we can consider each subset of mirror positions and find what is the disjoint subset of the same or one less size that gets us closest to our target. The key insight to make this a practical algorithm is to notice that the disjoint requirement is not necessary. If you place a mirror z in both subsets X and Y then X-{z} and Y-{z} forms a cheaper solution so these cases can never affect the minimum cost.
Overall this yields a fairly simple O(N * 2^N) algorithm
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Reflections {
public: long long solve(vector < int > & M, int P) {
int N = M.size();
// Compute the sum of each subset.
vector < long long > V[25];
for (int i = 0; i < 1 << N; i++) {
long long sum = 0;
for (int j = 0; j < N; j++)
if (i & 1 << j) sum += M[j] * 2 ll;
V[__builtin_popcount(i)].push_back(sum);
}
// For each subset find the subset of the same or one lesser size that puts us closest to our target.
long long ret = abs(P);
for (int i = 0; i <= (N + 1) / 2; i++) {
sort(V[i].begin(), V[i].end());
for (int j = 0; j < V[i].size(); j++) {
// Find subsets of equal size that put us close to P.
int pos = upper_bound(V[i].begin(), V[i].end(), V[i][j] - P) - V[i].begin();
if (pos < V[i].size()) ret = min(ret, 2 * i + abs(P - V[i][j] + V[i][pos]));
if (pos > 0) ret = min(ret, 2 * i + abs(P - V[i][j] + V[i][pos - 1]));
// Find subsets of one lesser size that put us close to P.
if (!i) continue;
pos = upper_bound(V[i - 1].begin(), V[i - 1].end(), V[i][j] - P) - V[i - 1].begin();
if (pos < V[i - 1].size()) ret = min(ret, 2 * i - 1 + abs(P - V[i][j] + V[i - 1][pos]));
if (pos > 0) ret = min(ret, 2 * i - 1 + abs(P - V[i][j] + V[i - 1][pos - 1]));
}
}
return ret;
}
long long minimumMoves(vector < int > X, vector < int > Y, vector < int > Z, vector < int > P) {
return solve(X, P[0]) + solve(Y, P[1]) + solve(Z, P[2]);
}
};
Both these solutions can be further sped up by eliminating binary search. For example, in the second solution that allows overlapping sets, instead of the inner j-based loop over V[i] we can do the following:
1
2
3
for (int other = i; other >= 0 && other >= i - 1; --other) { // the size of the subtracting set
ret = min(ret, join(V[i], V[other], P) + i + other);
}
with the join function defined as follows:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// with both A and B sorted, find smallest |elem(A)-elem(B)-X| in O(|A|+|B|)
long long join(const vector < long long > & A,
const vector < long long > & B, long long P) {
int i = 0;
int j = 0;
long long ret = my_abs(P); // this is "infinity"
while (i < (int) A.size() && j < (int) B.size()) {
ret = min(ret, my_abs(A[i] - B[j] - P));
if (A[i] - B[j] >= P) {
++j;
} else {
++i;
}
}
return ret;
}