
|
Match Editorial |
Wednesday, November 28, 2007
Match summary
The SRM 379 division 1 has ended with SnapDragon, marek.cygan and gozman taking the first three places. SnapDragon set a new SRM win record showing an outstanding performance and being the fastest to solve the 250. gozman and wata were the fastest to solve the 500 and 1000, respecively.
stephanie won the division 2 after 3 very fast submissions and 4 successful challenges. The second place went to Delusion who had a very fast 1000 pointer and the third place to serine with 6/7 successful challenges.
The Problems
DownloadingFiles

Used as: Division Two - Level One:
Value 250 Submission Rate 345 / 484 (71.28%) Success Rate 307 / 345 (88.99%) High Score wooyaggo for 245.35 points (3 mins 55 secs) Average Score 173.11 (for 307 correct submissions)
This problem can be solved with many different approaches. The problem statement gave the competitors the freedom to choose the method they like by distributing the available bandwidth however they want every time. However, one could notice that the required answer is actually the totalSizeLeft / totalBandwidth where totalSizeLeft is the sum of the products remainingTime[i]*speed[i] and totalBandwidth is the sum of the speeds of all files. So those who could read behind the lines had a fairly advantage against those who simulated the procedure.
Here is stephanie's quick submission. You can also check out lhchavez's solution for a simulation approach.
SellingProducts

Used as: Division Two - Level Two:
Used as: Division One - Level One:
Value 500 Submission Rate 334 / 484 (69.01%) Success Rate 167 / 334 (50.00%) High Score obellik for 483.09 points (5 mins 21 secs) Average Score 363.25 (for 167 correct submissions)
Value 250 Submission Rate 391 / 392 (99.74%) Success Rate 305 / 391 (78.01%) High Score SnapDragon for 248.48 points (2 mins 13 secs) Average Score 217.52 (for 305 correct submissions)
This problem required a simple iteration over every possible price and calculate the profit we can make. For a certain price p the profit is the sum of every positive difference p-cost[i] for every customer i that is willing to pay p or more. If two different prices give the same profit the smallest one must be kept. If we can't get a positive profit then the optimal price is 0.
TVGameWinnings

Used as: Division Two - Level Three:
Value 900 Submission Rate 51 / 484 (10.54%) Success Rate 28 / 51 (54.90%) High Score lhchavez for 570.05 points (24 mins 52 secs) Average Score 453.37 (for 28 correct submissions)
In this game, the player can't choose two dominoes from the same row or the same column. Without loss of generality we can consider that the player picks the rows in order starting from the first one and then chooses a domino from a column he hasn't chosen yet. By this procedure it is clear that the player is actually choosing a permutation of the columns. Since the maximum number of columns is 6 there are only 6!=720 different ways to pick the n dominoes so we can use brute force and try them all. Contestants that use C++ could use the next_permutation function of STL otherwise they had to write their own function for generating permutations.
For a given permutation p we are calculating the product of all elements board[i,p[i]]. Now all
that is left to find is whether or not to multiply this product by -1. To find this we must count the number
of cycles in our permutation. To do this consider the following algorithm:
mark every element of the permutation as unvisited
cycleCount = 0
while there exists an unvisited element i
Iterate through the cycle i->p[i]->p[p[i]]->..->i and
mark every reached element as visited
Increase cycleCount by 1
return cycleCount
If cycleCount is even multiply the product of the numbers by -1 and update the minimum and maximum values.See Delusion's solution for an implementation of this approach. FillBox


Used as: Division One - Level Two:
Value 500 Submission Rate 221 / 392 (56.38%) Success Rate 88 / 221 (39.82%) High Score gozman for 479.09 points (5 mins 59 secs) Average Score 265.15 (for 88 correct submissions)
There were many different approaches that contestants used to solve this problem. I will describe the one that was used by gozman. This solution takes the cubes in decreasing order of size and at each point places as many as possible. The maximum number of cubes of size p that can be placed in the box is K=[L/p]*[W/p]*[H/p], where [x]=floor(x). Considering that we have already covered a volume V by using larger cubes, the maximum number of cubes that can be placed is M = K - V/(p^3) (V/(p^3) is the volume measured in p^3 cubes, V is always divisible by p^3 since the volume of every cube larger than p is divisible by p^3). If we have less cubes at this point we will use those instead. At the end, the required number of cubes of size 1 will be equal to the remaining volume. If we have fewer of those cubes then there is no solution.
This solution always finds the (unique) optimal solution S. Suppose that there is another solution S' that uses the same number of 2^j-cubes for all j>i but uses less 2^i-cubes. Then we can always reach S' from S by breaking larger cubes into smaller ones so this solution would use more cubes and it wouldn't be optimal.
Other methods first calculate the minimum number of cubes needed to cover the whole box supposing we have an infinite number of cubes and then iteratively breaking them into smaller ones until they reach a feasible solution.
TVGame

Used as: Division One - Level Three:
Value 1000 Submission Rate 36 / 392 (9.18%) Success Rate 11 / 36 (30.56%) High Score wata for 698.42 points (20 mins 38 secs) Average Score 576.62 (for 11 correct submissions)
This problem is similar to the one used for div2 900 but here we must calculate the sum of every possible outcome instead of finding the minimum and maximum values. Here, the constraints are much higher (N<=50) so brute force would take astronomically long time to compute. However, we are able to solve several cases in polynomial time. So what we should try to do is to reduce the other cases to them. Here are two special cases that we are able two solve:
Case 1: Our matrix is triangular. Then every possible choice of n dominoes (besides the main diagonal) would include a 0 (so its outcome would be 0). Choosing the numbers of the main diagonal would give an outcome equal to the product of those numbers multiplied by -1 if N is even. That is because every domino of the main diagonal is a cycle by itself.
Case 2: Our matrix has two rows i1, i2 where Row_i1 = k*Row_i2. Then if we chose domino (i1,j1) and domino (i2,j2) the product of the hidden numbers would be the same as choosing dominoes (i1,j2) and (i2,j1) instead, but the number of cycles in those two choices would differ by one because by swaping those elements we would either break a cycle into two or join two cycles together. Either way the sign of the two products would be different. So for every possible outcome there exists its negative one. Summing those outcomes altogether gives us 0.
You can easily see now that if we add a row multiplied by some number to another one the answer remains the same.
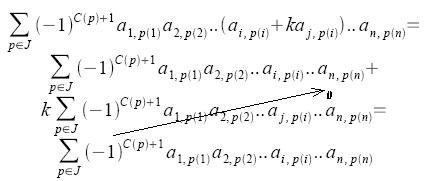
Here J is the set of permutations (possible choices) and C(p) is the number of cycles in the permuation.
The erased term is equal to 0 because we have two equal rows.
Also swaping two rows i, j changes the sign of the answer (add row i to row j, subtract j from i, add i to j).
Now you can see that we can apply Gaussian Elimination to our matrix and reduce it to a triangular. Every addition, subtraction and multiplication however must be done mod 121547. Divisions turn into multiplications with the inverses (mod 121547) which can be calculated by the Extended-Euclidean algorithm. The whole process is very similar to determinant calculation. They only differ at the last part because here we have to multiply by -1 if N is even. So the required answer is actually (-1)^(N+1)*determinant.
Homework: After those observations can you find an O(2^N) algorithm for solving the div2 900?